Для систем нелинейных дифференциальных уравнений с медленно меняющимися коэффициентами в случае простого нулевого корня у характеристического уравнения построены формальные частных решения, обладающие асимптотическим свойством.
Данная работа посвящена исследованию системы нелинейных дифференциальных уравнений нейтрального типа с медленно меняющимися коэффициентами вида
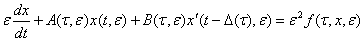 (1)
(1)
где х, 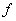 -n- мерные векторы, из них х(
-n- мерные векторы, из них х(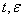 ) –неизвестные, А(
) –неизвестные, А(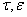 ), В(
), В(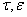 ) — квадратные матрицы n-го порядка допускающие формальные разложения
) — квадратные матрицы n-го порядка допускающие формальные разложения
А(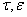 ) =
) =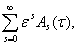 В(
В(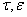 ) =
) =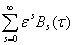 (2)
(2)
причем 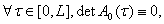
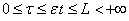 медленное время,
медленное время, 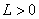 –фиксированное число
–фиксированное число 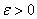 малый параметр,
малый параметр, 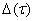 функция неотрицательна и удовлетворяет условию
функция неотрицательна и удовлетворяет условию
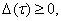
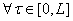 (3)
(3)
вектор 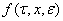 разлагается в ряд Тейлора в окрестности точки
разлагается в ряд Тейлора в окрестности точки 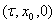 .
.
Такие уравнения представляют значительный теоретический и практический интерес. При решении этой системы в отличие от систем запаздывающего типа, возникает специфические трудностей, обусловленные наличием в уравнений производной при различных значениях аргумента. Одной из таких трудностей является, например, требование, чтобы искомое решение было дифференцируемым. Еще более серьезные трудности возникают при построении решений системы дифференциальных уравнений нейтрального типа в случае переменного отклонения аргумента.
Как известно [1], при переменном запаздывании метод шагов может оказаться неприменим.
При следовании системы (1) рассмотрим так называемый критические случай по Като [2].
Построение асимптотического решения системы (1) существенным образом зависят от поведения корней уравнения
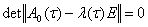 (4)
(4)
(Е-единичная матрица n-го порядка) которое называют характеристическом для матрицы 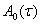 корни этого уравнения обозначим через
корни этого уравнения обозначим через 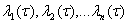 .
.
Рассмотрим случай, когда корень уравнения (4) для всех 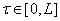 остается простым. Тогда справедлива
остается простым. Тогда справедлива
Теорема 1. Пусть выполняются условия
а) матрицы 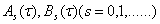 при
при 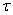
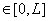 , а вектор
, а вектор 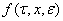 в области
в области 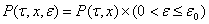 где
где 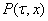 - некоторая область пространства переменных
- некоторая область пространства переменных 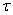 ,х принадлежащих классу ск (для достаточно больших значении к);
,х принадлежащих классу ск (для достаточно больших значении к);
б) при 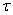
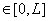 ,
, 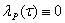
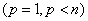
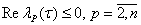 , т, е матрица А0 (
, т, е матрица А0 (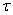 ) имеет простое собственное значение;
) имеет простое собственное значение;
в) 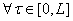 , элементы матрицы
, элементы матрицы 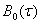 ,
, 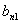
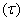 отлично от нуля
отлично от нуля
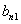
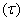
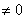 (5)
(5)
Тогда уравнение (1) имеет формальные частные решение вида
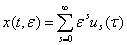 (6)
(6)
Для доказательство теоремы-1, подставляем (6) в систему (1), раскладываем вектор 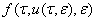 в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки 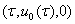 и в полученном разложении собираем члены с одинаковым степенями
и в полученном разложении собираем члены с одинаковым степенями 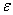 , получаемся отношение
, получаемся отношение
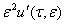 +
+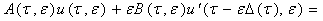
=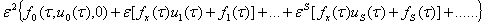 (7)
(7)
Здесь элементы матрицы 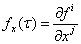 и компоненты вектора
и компоненты вектора 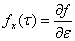 вычисляются в точке
вычисляются в точке 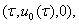 а вектор
а вектор 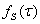 выражается определенным образом через
выражается определенным образом через 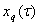
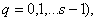
Прежде чем определить коэффициенты ряда (6), разложим в формальные ряды по степеням параметра 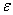 вектор
вектор 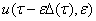
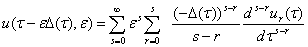 (8)
(8)
Учитывая (8) в уравнение (7) приравнивая коэффициенты при одинаковых степенях параметра 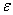 , получим уравнения, из которых определяются неизвестные элементы разложения (6).
, получим уравнения, из которых определяются неизвестные элементы разложения (6).
Так при 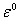 имеем уравнение:
имеем уравнение:
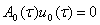 (9)
(9)
из которого согласно [3] находим
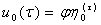 , (10)
, (10)
где 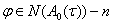 мерный вектор, для которого первая компонента равна единице, остальные нулю,
мерный вектор, для которого первая компонента равна единице, остальные нулю, 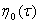 -произвольная, отличная от нуля
-произвольная, отличная от нуля 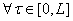 функция определяющаяся на следующим шаге.
функция определяющаяся на следующим шаге.
При 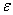 в системы имеем неоднородные уравнения вида
в системы имеем неоднородные уравнения вида
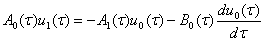 (11)
(11)
Учитывая (10) уравнение (11) запишем в виде
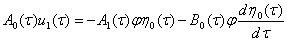 . (12)
. (12)
Для того, чтобы уравнение (12) имело решение, необходимо и достаточно, чтобы правая часть этого уравнения было ортогональным решением союзной системе однородной части, т.е 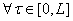 выполнялось со отношение
выполнялось со отношение
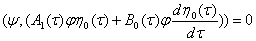 (13)
(13)
где 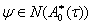 n-мерный вектор n-ная координата равна единице остальные равны нулю,
n-мерный вектор n-ная координата равна единице остальные равны нулю, 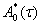 -матрица комплексно сопряжённая к матрице
-матрица комплексно сопряжённая к матрице 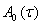 .
.
Равенство (13) запишем в следующем виде
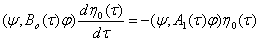 (14)
(14)
Интегрируя уравнения (14), при этом учитывая (5) определим неизвестную функцию 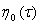
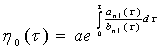 (15)
(15)
В равенстве интегрирующий множитель считаем а=1. Тогда имеем
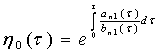 . (16)
. (16)
Так как для уравнение (12) выполнятся, условия (13) то находим
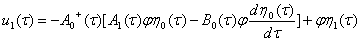 (17)
(17)
где 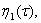
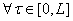 неизвестная функция, определяющаяся на следующем шаге
неизвестная функция, определяющаяся на следующем шаге 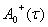 -обобщенно-обратная матрица к матрице
-обобщенно-обратная матрица к матрице 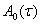 .
.
При 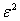 из (7) с учетом (8) получаем
из (7) с учетом (8) получаем
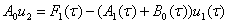 (18)
(18)
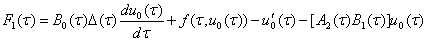 .
.
Для уравнения (18) с учетом (17) условие разрешимости имеет вид
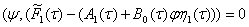 ,
, 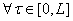 (19)
(19)
Так как 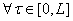 ,
, 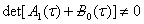 то из (19) определим неизвестная функция
то из (19) определим неизвестная функция 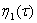
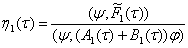 . (20)
. (20)
Условия (19)для уравнения (18) выполняются, тогда из (18) находим неизвестный вектор 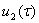 ряда (5)
ряда (5)
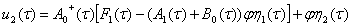 , (21)
, (21)
где 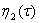 -неизвестная функция, которая определяется на следующем шаге.
-неизвестная функция, которая определяется на следующем шаге.
Аналогично продолжив этот процесс можно определить неизвестные элементы 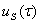 ряда (5). Теорема доказана.
ряда (5). Теорема доказана.
Описанный выше алгоритм дает возможность определить любой член разложения (5). Обычно на практике из-за громоздкости вычислений приходится ограничиваться построением первых m членов разложения (5). В связи с этим в рассмотрение вводится при помощи х выражения
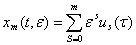 (22)
(22)
m-тое приближение к искомым решениям системы (1).
Пусть х(t,ε) представляет собой точное решение системы (1), удовлетворяющее при t=0 тем же начальным условиям что и х(t,ε), т.е
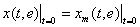 (23)
(23)
Тогда можно показать, что приближенное решение 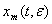 асимптотически сходится к точному решению х(t,ε).
асимптотически сходится к точному решению х(t,ε).
Для получения оценки нормы разности будет использована.
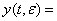
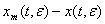 (24)
(24)
Лемма 1. Если матрица 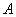
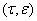 допускает разложения
допускает разложения
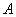
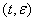
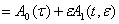 , (25)
, (25)
где матрицы 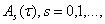 на отрезки
на отрезки 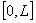 неограниченно дифференцируемы и кроме того для любого n-мерного вектора z справедливо неравенство
неограниченно дифференцируемы и кроме того для любого n-мерного вектора z справедливо неравенство
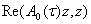 ≤0, (26)
≤0, (26)
то для решения уравнения
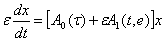 (27)
(27)
с начальным условием 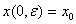 на отрезке
на отрезке 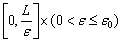 имеет место оценка
имеет место оценка
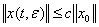 (28)
(28)
где с- некоторая положительная константа, не зависящая от 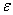 .
.
Доказательство леммы можно найти в работе [3].
Асимптотический характер форельных частных решений устанавливает.
Теорема 2. Пусть для системы дифференциальных уравнении (1) выполнены условия теоремы 1 и следующие:
1) уравнений (4) имеет простой корень с неположительной вещественной частью
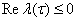 ,
, 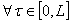 (29)
(29)
2) вектор
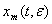 определяемый равенствам (28), на начальном множестве
определяемый равенствам (28), на начальном множестве 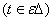 совпадает с точным решением системы (1)
совпадает с точным решением системы (1)
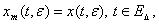 (30)
(30)
3) функция 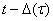 растет старого монотонно на отрезке
растет старого монотонно на отрезке 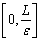 , причем
, причем
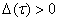

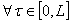 . (31)
. (31)
4) 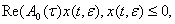
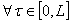 . (32)
. (32)
5) вектор — функция 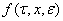 удовлетворяет условно Лепщица с постоянной l:
удовлетворяет условно Лепщица с постоянной l:
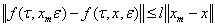 (33)
(33)
Тогда существуют постоянные 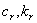 не зависящие от
не зависящие от 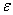 такие, что для всех
такие, что для всех 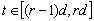 где
где 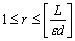 и
и
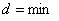
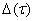 ,
, 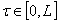 (34)
(34)
справедливы неравенства
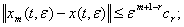 (35)
(35)
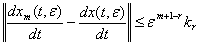 .
.
Доказательство. Подставляя в дифференциальное уравнение (1) вектор (22) и учитывая (29) получим.
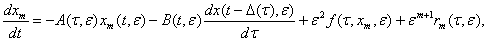 (36)
(36)
где 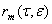 - вектор равно мерно ограниченный в окрестности точки
- вектор равно мерно ограниченный в окрестности точки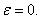 Тогда вектор (24) удовлетворяет следующей системе дифференциальных уравнений
Тогда вектор (24) удовлетворяет следующей системе дифференциальных уравнений
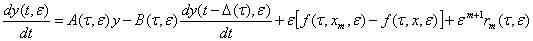 , (37)
, (37)
причем согласно (30)
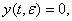
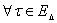 (38)
(38)
Обозначим через 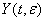 нормированную фундаментальную матрицу системы
нормированную фундаментальную матрицу системы
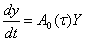 (39)
(39)
т. е. такое решение рассматриваемой системы, при котором 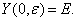 С учётом (37) на произвольном r-м шаге
С учётом (37) на произвольном r-м шаге 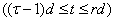 эквивалентно следующей интегральной системе:
эквивалентно следующей интегральной системе:
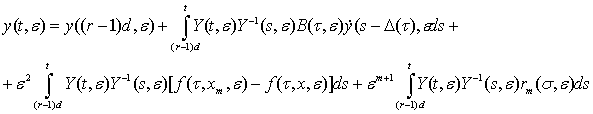 , (40)
, (40)
где 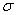 =
=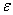 s. Если теперь принять во внимание (32) и применить лемму-1, то придем к выводу что
s. Если теперь принять во внимание (32) и применить лемму-1, то придем к выводу что
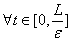 u
u 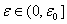
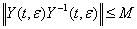 (41)
(41)
где М-не зависящая от 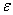 постоянная. Оценивая по норме векторы и матрицы, входящие в (40), учитывая (33) получаем неравенство
постоянная. Оценивая по норме векторы и матрицы, входящие в (40), учитывая (33) получаем неравенство
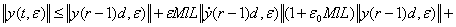
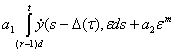 (42)
(42)
где 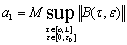 ,
, 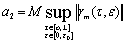 .
.
Очевидно, что теорема справедлива на первом шаге 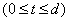 . В самом деле, из (42) на основании (38) следует
. В самом деле, из (42) на основании (38) следует
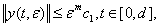 (43)
(43)
где 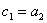 . Теперь из (37)находим
. Теперь из (37)находим
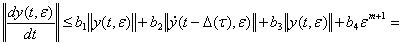
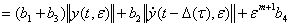 (44)
(44)
где 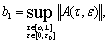
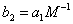 ,
, 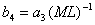 (45)
(45)
Учитывая (43) и (44), для производной 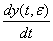 на первом шаге получаем оценку
на первом шаге получаем оценку
 , (46)
, (46)
где 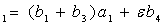
Докажем теперь справедливость теоремы на втором шаге 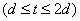 . Принимая во внимание оценки (44) и (46), из (42) на втором шаге имеем
. Принимая во внимание оценки (44) и (46), из (42) на втором шаге имеем
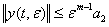 (47)
(47)
где 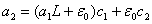 . Аналогично из (44) получаем оценку производной на втором шаге
. Аналогично из (44) получаем оценку производной на втором шаге
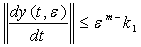 (48)
(48)
где 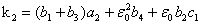 .
.
Далее, методом математической индукции утверждение теоремы обобщается на произвольный шаге. Действительно, пусть теорема верна для r-го шага 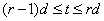 , т.е существуют не зависящие от ε постоянные
, т.е существуют не зависящие от ε постоянные 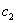 и
и 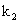 такие, что
такие, что
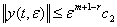
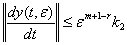 ,
, 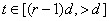 (49)
(49)
Тогда для (r+1)- го шага 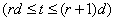 из (43) и (44) получим
из (43) и (44) получим
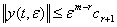 ;
;
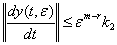 (50)
(50)
где 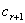 =
=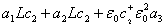 ,
, 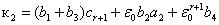 )
)
Отсюда заключаем, что теорема верна для произвольного 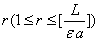 , что и требовалось доказать.
, что и требовалось доказать.
Литература:
1. Като. Т. Теория возмущений линейных операторов. М. Мир 1972.740 с
2. Алишев. А. Решение нелинейных дифференциальных уравнений дробного ранга. –ДАН; УССР, сер.А № 6. 1982. с.6–9.
3. Фищенко С.Ф, Шкиль. Н.И, Николенко А. Д. Асимптотические методы в теории линейных дифференциальных уравнений. Киев: Наук. думка, 1966–252 с.

