Рассматриваются вопросы разрешимости сингулярных интегральных уравнений с дробно-линейным сдвигом Карлемана в случае, когда коэффициенты уравнения рациональные функции.
The article discusses the solvability of singular integral equations with a fractional-linear Carleman shift in the case when the coefficients of the equation are rational functions.
Пусть Г — простая замкнутая кривая Ляпунова и ![]() совокупность всех определенных на Г функций
совокупность всех определенных на Г функций ![]() , удовлетворяющих условию Гелъдера с показателем
, удовлетворяющих условию Гелъдера с показателем ![]() , т. е. таких что
, т. е. таких что ![]() (t)-
(t)-![]() (
(![]() )|
)|![]() А
А ![]() , A-const для всех t,
, A-const для всех t,![]()
![]() Г. Для
Г. Для ![]() (t)
(t)![]() (Г) норму определяем соотношением
(Г) норму определяем соотношением
![]() =max|
=max|![]() (t)|+sup
(t)|+sup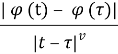 , t,
, t,![]()
Через ![]() (Г) (соотв.
(Г) (соотв. ![]() (Г)) обозначаем пространство всех функций
(Г)) обозначаем пространство всех функций ![]()
![]() , допускающих аналитическое продолжение в областъ
, допускающих аналитическое продолжение в областъ ![]() (соотв.
(соотв. ![]() , и обращающихся в нуль на бесконечности).
, и обращающихся в нуль на бесконечности).
Рассмотрим интеграл типа Коши.
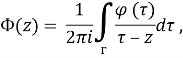 z
z![]()
и оператор сингулярного интегрирования S, определяемый
(S![]() )(t) =
)(t) = ![]()
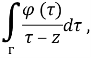 t
t![]() (1.1)
(1.1)
где интеграл понимается в смысле главного значения по Коши. ![]() называется плотностью интеграла. Через w обозначим оператор, действующий по правилу (
называется плотностью интеграла. Через w обозначим оператор, действующий по правилу (![]() )(t)=
)(t)=![]() . Функция
. Функция ![]() называется функцией сдвига. Говорят, что сдвиг удовлетворяет условие Карлемана, если
называется функцией сдвига. Говорят, что сдвиг удовлетворяет условие Карлемана, если ![]() (t)=t, t
(t)=t, t![]() Г, где
Г, где ![]() (t)=
(t)=![]() ,
, ![]() =t, k=1,2,3,…n.
=t, k=1,2,3,…n.
Рассмотрим оператор T=![]() , где C=
, где C=![]() D=
D=![]() функциональные операторы,
функциональные операторы, ![]() -рациональные функции, а
-рациональные функции, а ![]() — взаимно дополнительные проэкторы в пространстве
— взаимно дополнительные проэкторы в пространстве
![]()
![]()
![]()
Пусть Г0 = {t: |t| = 1} единичная окружность, ![]() — сохраняющая ориентацию, удовлетворяющий условию Карлемана (n = 2) дробной-линейный сдвиг единичной окружности Г0 на себя,
— сохраняющая ориентацию, удовлетворяющий условию Карлемана (n = 2) дробной-линейный сдвиг единичной окружности Г0 на себя,
![]() =
= ![]() , |
, |![]() | < 1
| < 1
Обозначим ![]() =
= ![]() ,
, ![]() +(t) =
+(t) = ![]() + =
+ = ![]() ,
, ![]() -(t) =
-(t) = ![]() - =
- = ![]()
Тогда, функция ![]() представима в виде
представима в виде ![]() =
= ![]() +(t) t
+(t) t![]() -(t),
-(t),
где ![]()
![]() ,
, ![]()
![]() , причём.
, причём. ![]() [
[![]() ] =
] = ![]() (t),
(t), ![]() - [
- [![]() ] =
] = ![]() .
.
Рассмотрим функциональный оператор
A = p(t)J + q(t)W, где р(t), q(t) — рациональные функции.
Предположим, что
![]() А(t) = p(t)p [
А(t) = p(t)p [![]() ] — q(t)q [
] — q(t)q [![]()
![]()
Тогда, оператор А, а вместе с ним, и соответствующая ему матрица-функция
A(t)![]()
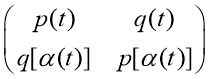
непрерывно обратимы.
Определение. Под факторизацией матрицы-функции G(t), определенной на замкнутом контуре Г0, понимается представление G(t) в виде
G(t) = G+(t) ![]() G-(t), (1)
G-(t), (1)
где G±(t) суть граничные значения матрицы-функции, аналитических и невырожденных в D±, ![]() = diag{
= diag{![]() }k1, k2 называются частными индексами матрицы G(t).
}k1, k2 называются частными индексами матрицы G(t).
Так как матрица A(t) рациональная, она допускает факторизацию вида (1) (см.![]() ). При факторизации рациональных матриц-функций существенную роль играет следующая Лемма. Пусть м. –ф. B(z) аналитична в области D(
). При факторизации рациональных матриц-функций существенную роль играет следующая Лемма. Пусть м. –ф. B(z) аналитична в области D(![]() 0) и det B(
0) и det B(![]() 0) = 0. Тогда B = CU. Где м. –ф. С аналитична в области D, имеет те же (с учетом кратности) нули определителя, что и В, за исключение точки
0) = 0. Тогда B = CU. Где м. –ф. С аналитична в области D, имеет те же (с учетом кратности) нули определителя, что и В, за исключение точки ![]() 0, где кратность нуля det C на единицу меньше, чем det B, а
0, где кратность нуля det C на единицу меньше, чем det B, а
U(z) = 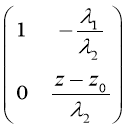
𝛌1, 𝛌2 — некоторые числа.
Действительно, при z≠z0 матрица U(z) обратима и обратная к ней матрица имеет вид
V(z) = U-1(z) = 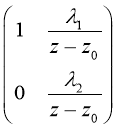
Положим при ![]() . Так как det C =
. Так как det C = ![]() detB, а м.–ф. U-1(z) аналитична в плоскости с выколотой точкой
detB, а м.–ф. U-1(z) аналитична в плоскости с выколотой точкой ![]() 0, остаётся добиться того, чтобы м.–ф. C(z) была аналитична в точке
0, остаётся добиться того, чтобы м.–ф. C(z) была аналитична в точке ![]() 0. Если
0. Если ![]() (i,j=1,2) элементы м.–ф. С и B то
(i,j=1,2) элементы м.–ф. С и B то ![]()
![]()
![]() =
= 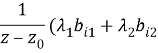 ).
).
Таким образом, для аналитичности матрицы C(z) необходимо и достаточно, чтобы столбцы матрицы B(z) (при ![]() ) были линейно зависимы, а
) были линейно зависимы, а ![]() (i=1,2) коэффициенты линейной комбинации.
(i=1,2) коэффициенты линейной комбинации.
Так как det B(z0) = 0, то такие ![]() существуют.
существуют.
Обозначим теперь ![]() A(t) = det A(t), и пусть
A(t) = det A(t), и пусть
![]() A(t) =
A(t) = 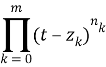
![]() 0(t) ≠ 0, t
0(t) ≠ 0, t![]() 0, zk
0, zk![]() D+, k=1,2,…,m.
D+, k=1,2,…,m.
Пусть k=0. Умножая матрицу A(t) справа на V(z) получаем
A(t) = 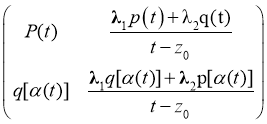
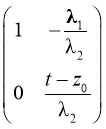 = B0U0
= B0U0
Для того чтобы м.–ф. B0(t) была аналитична в D+, очевидно, достаточно взять ![]() =q(z0),
=q(z0), ![]() =-p(z0). Тогда, det B0 в точке z=z0 имеет нуль порядка n0–1. Эту же процедуру проделаем теперь для матрицы B0 и получаем B0 = B1U1, где
=-p(z0). Тогда, det B0 в точке z=z0 имеет нуль порядка n0–1. Эту же процедуру проделаем теперь для матрицы B0 и получаем B0 = B1U1, где
U1=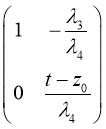
и det B1 имеет нуль порядка n0–2 в точке z0. Повторяя этот процесс n0 раз мы получаем представление A(t) = ![]() U, где U=
U, где U=![]() и det
и det ![]() не обращается в нуль в точке z0. Этот же процесс повторяем теперь для точки
не обращается в нуль в точке z0. Этот же процесс повторяем теперь для точки
z1, z2, z3,…,zm и получаем представление
A(t)=A+(t)![]() (t)A-(t) (2)
(t)A-(t) (2)
где A+(t) (A-(t)) — рациональная м. –ф., все полюса элементов и нули определителя, которые сосредоточены в D- (в D+). ![]() (t) — диагональная матрица
(t) — диагональная матрица ![]() (t) = diag {
(t) = diag {![]() }.
}. ![]() — частные индексы матрицы A(t).
— частные индексы матрицы A(t).
Обозначим
A+(t) = 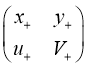 , A-(t) =
, A-(t) = 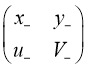
Следуя (7), если м.–ф. A(t) допускает факторизацию вида (2), то функциональный оператор A=p(t)J + q(t)W представляется в виде
A=A+RA- (3)
где оператор A+, A- и R соответственно имеют вид:
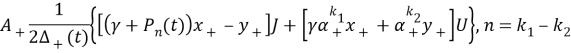
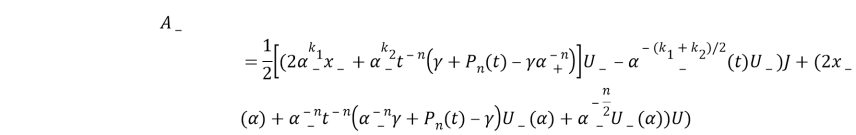
R=![]()
При этом, операторы A+ и A- удовлетворяют условиям ![]()
![]()
![]() ,
, ![]() , (4)
, (4)
![]() — постоянная,
— постоянная, ![]() и
и ![]() не обращается в нуль на Г0, полином степени n = k1 — k2, удовлетворяющий условию
не обращается в нуль на Г0, полином степени n = k1 — k2, удовлетворяющий условию ![]() , а оператор U = —
, а оператор U = — ![]() т. е.,
т. е., ![]()
Рассмотрим теперь оператор
T = CP+ + DP-, где C=![]()
Обозначим![]() , тогда в силу (3), оператор представим в виде
, тогда в силу (3), оператор представим в виде
![]()
или в силу (4)
![]()
![]()
Операторы C, A+ и ![]() непрерывно обратимы, причём
непрерывно обратимы, причём
![]()
И следовательно, обратимость оператора Т зависит от обратимости оператора ![]() .
.
Рассмотрим различные случаи.
1) Пусть k1=0, k2=0. Тогда, можно положить R=J и оператор Т непрерывно обратим и ![]() обратный для него оператор.
обратный для него оператор.
2) Пусть k1<0. Тогда, как видно из (3) коэффициенты функционального оператора принадлежат ![]() и следовательно, оператор R удовлетворяет условию
и следовательно, оператор R удовлетворяет условию ![]()
И, следовательно, (см.![]() ) Т обратим слева и его левый обратный имеет вид
) Т обратим слева и его левый обратный имеет вид
![]()
в частности, dim Ker T=0.
3) Пусть k1>0, k1<0. Тогда (см.![]() ) функции
) функции ![]() k=0,1…., [k1/2], где
k=0,1…., [k1/2], где
![]()
образует базис ядра оператора Т.
4) Если k1>0, k2>0, то коэффициенты функционального оператора R принадлежат ![]() и следовательно, удовлетворяют условию
и следовательно, удовлетворяют условию ![]() . Отсюда, оператор
. Отсюда, оператор ![]() обратим справа и
обратим справа и ![]() его правый обратный. Поэтому, оператор Т обратим справа и его правый обратный имеет вид
его правый обратный. Поэтому, оператор Т обратим справа и его правый обратный имеет вид ![]()
Литература:
- Литвинчук Г. С. Краевые задачи и сингулярные интегральные уравнения со сдвигом. — Издательство «Наукa», Главная редакция физико-математической литературы, 1977.
- Карапетянц Н. К., Самко С. Г. Уравнения с инволютивными операторами и их приложения. — Изд-во Рост. ун-та, 1988.
- Мусхелишвили Н. И. Сингулярные интегральные уравнения, М., 1968 //Институт математики Поступило им. ВИ Романовского. — 1973. — Т. 25.
- Литвинчук Г. С., Спитковский И. М. Факторизация матриц-функций //М.: ВИНИТИ. — 1984.
- Гохберг И. Ц., Крупник Н. Я. Введение в теорию одномерных сингулярных операторов //Кишинев: Штиинца. — 1973.
- Гахов Ф. Д. Краевые задачи. — Главная редакция физико-математической литературы издательства “Наука”, 1977.
- Кравченко В.Г, Шаев А. К. Теория разрешимости сингулярных интегральных уравнений с дробно-линейным сдвигом Карлемана. ДАН СССР, 1991, том 316, № 2.

