В данной работе исследуется эквивалентность уравнения смешанного типа симметрической системы первого порядка.
Рассмотрим следующую задачу:
Характеристическая задача:
![]() (1)
(1)
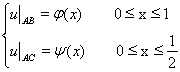 (2)
(2)
![]() (3)
(3)
Здесь, ![]() дифференциальный оператор,
дифференциальный оператор, ![]() , A(0;0), B(1;0), C
, A(0;0), B(1;0), C![]() . Задача рассматривается в следующем ABC характеристическом треугольнике (рис. 1).
. Задача рассматривается в следующем ABC характеристическом треугольнике (рис. 1).
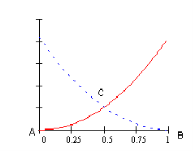
Рис. 1. Характеристический треугольник
Покажем эквивалентность этого уравнения симметрической системе первого порядка.
Для решение задачи (1)-(2) вводим вспомогательную функцию:
![]() , здесь
, здесь ![]()
В итоге для функции ![]() получим следующую задачу:
получим следующую задачу:
![]() (4)
(4)
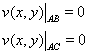 (5)
(5)
Здесь, 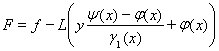
Вводим следующие обозначения: 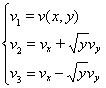
Получим задачу Коши для следующий симметрической системе:
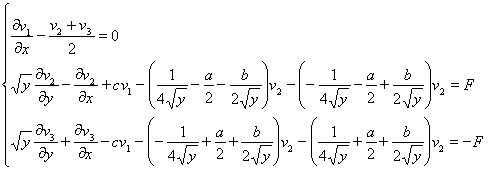 (6)
(6)
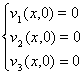 (7)
(7)
Запишем задачу в матричной форме:
![]()
здесь,
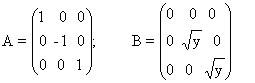
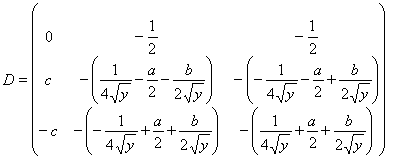 ;
; 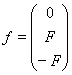 ;
;
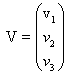 — неизвестная вектор-функция.
— неизвестная вектор-функция.
Полученная система гиперболического типа. Действительно по определению характеристик ([1])
![]()
Значить, заданная задача эквивалентна задачи Коши для уравнений симметрической гиперболической системы.
Верна следующая теорема:
Теорема. Для того чтобы задача для уравнений смешанно-составного типа имела решения, необходимо и достаточно, чтобы имела решения задача Коши для уравнений симметрической системы.
Литература:
- Годунов С. К. Уравнения математической физики. М. «Наука». 1971. -416 с.
- Владимиров В. С. Уравнения математической физики. M.”Наука”1971.
- Тихонов А. Н., Самарский А. А. Уравнения математической физики. M.”Наука”1972
- Салохиддинов М. С. Уравнения математической физики (на узбекском языке). Т., «Узбекистон», 2002, 448 с.
- Т. Ж. Жураев, С.Абдиназаров. Уравнения математической физики (на узбекском языке). Т.2003. 332 с.

