Магнитная реверсивная фокусирующая система (МРФС) является промежуточным классом фокусирующих систем между системами с однонаправленным магнитным полем и магнитными периодическими фокусирующими системами (МПФС) и обеспечивает возможность качественной фокусировки электронных пучков при большой длине регулярной части СВЧ прибора О-типа [1, 2].
В статье [3] рассмотрена аппроксимация продольного распределения магнитного поля МРФС модернизированной вейвлет-функцией «Французская шляпа» (рис.1).
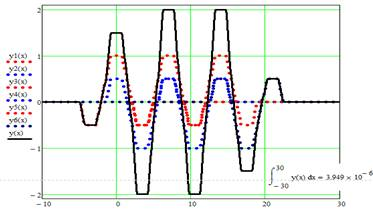
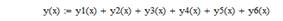
Рис. 1. Продольное распределение магнитного поля МРФС, состоящее из 6 чередующихся магнитов при М=1, L=2, d=3 [3]
Фактически МРФС предназначены для фокусировки протяженных электронных потоков, когда стремятся сохранить достоинства фокусировки однородным магнитным полем и уменьшить известные недостатки МПФС.
Авторами предложено несколько методов аппроксимации продольного распределения магнитного поля МРФС:
- суммой двух вейвлет-функций Гаусса второго порядка со смещением S относительно их максимумов [4] (рис. 2). Предложенный метод имеет основной недостаток — невозможность получения длинной «горизонтальной» площадки, что необходимо при ограниченном количестве реверсов магнитного поля;
а) S=1,4 б) S=1,5 в) S=1,6
Рис. 2. Суммирующее распределение (сплошная линия) из двух вейвлет-функций Гаусса второго порядка с различным значением смещения S [4]
- сложением двух функций: модернизированной вейвлет-функции «Французская шляпа» и двух вейвлет-функций Гаусса первого порядка.
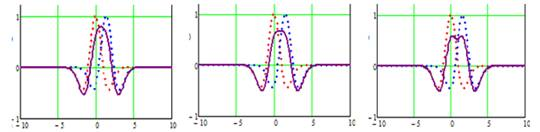
Рассмотрим предложенный метод на примере вейвлет-функции «Французская шляпа» (будем считать, что протяженность области реверса незначительна, что соответствует минимальному влиянию данной области на расфокусировку электронного потока). В этом случае формирование суммирующего распределения происходит путем наложения на вейвлет-функцию «Французская шляпа» (рис. 3б, линия 1) двух вейвлет-функций Гаусса первого порядка (рис. 3а), при этом последние разрываются в точке перегиба и сдвигаются в начало «горизонтальных» площадок первой вейвлет-функции.
а) б)
Рис. 3. Суммирующее распределение (б, линия 2), состоящее из вейвлет-функции «Французская шляпа» (б, линия 1) и двух вейвлет-функций Гаусса первого порядка (а)
Приняв полученное суммирующее распределение (рис. 3б, линия 2) за продольное распределение магнитного поля ячейки МРФС, получим продольное распределение магнитного поля МРФС, состоящей из 7 магнитов (рис. 4).
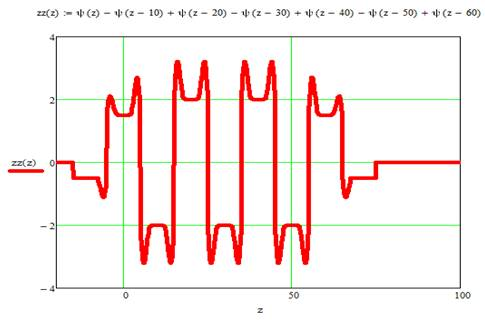
Рис. 4. Продольное распределение магнитного поля МРФС, состоящее из 7 чередующихся магнитов
Заменив вейвлет-функцию «Французская шляпа» модернизированной вейвлет-функцией «Французская шляпа» [3] и добавив вейвлет-функции Гаусса первого порядка по аналогии, получим ячейки МРФС с различной полярностью (рис. 5).
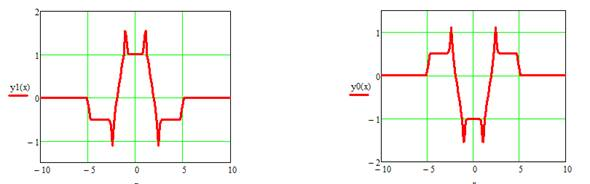
а) б)
Рис. 5. Распределение магнитного поля ячеек МРФС различной полярности при следующих параметрах М=1, L=5, d=1 с коэффициентом сжатия для вейвлет-функции Гаусса первого порядка k=7
На основании полученных распределений ячеек МРФС (рис. 5) сформируем МРФС (рис. 6, сплошная линия), состоящую из 6 магнитов c данными параметрами и коэффициентом сжатия для вейвлет-функции Гаусса первого порядка равным 7.
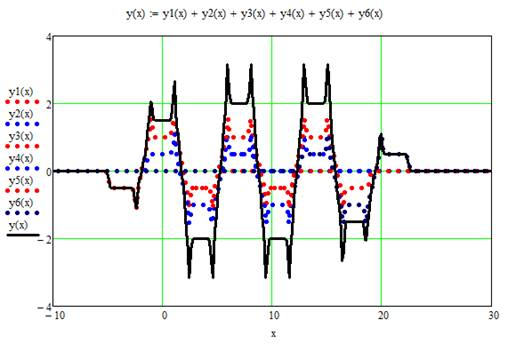
Рис. 6. Продольное распределение МРФС из 6 магнитов при следующих параметрах М=1, L=5, d=1 с коэффициентом сжатия для вейвлет-функции Гаусса первого порядка k=7
В дальнейшем планируется изучение взаимосвязи коэффициента сжатия вейвлет-функции Гаусса первого порядка k от свойств магнита и определения границы применения. Например, если взять такие же параметры магнита, как приведены выше, но изменить значения k (k = 3), то суммирующие распределения ячеек МРФС (рис. 7а — б) и продольное распределение магнитного поля МРФС изменят вид (рис. 8).
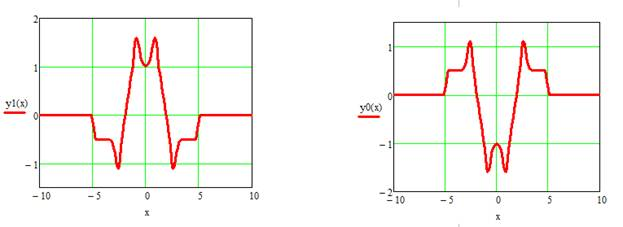
а) б)
Рис. 7. Суммирующее распределение ячеек МРФС различной полярности при следующих параметрах М=1, L=5, d=1 с коэффициентом сжатия для вейвлет-функции Гаусса первого порядка k=3
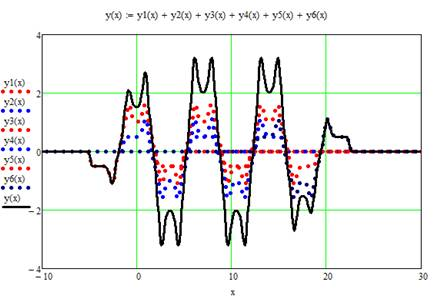
Рис.8. Продольное распределение магнитного поля МРФС, состоящее из 6 магнитов (рис. 7а-б) при k = 3
Полученные результаты показывают на эффективность применения вейвлет-функций при моделировании распределения магнитных полей в реверсивных магнитных фокусирующих системах с минимальной областью реверса. Кроме того, представляется возможность формировать области с максимальными амплитудами магнитного поля до и после реверса, что, как известно, способствует уменьшению дефокусирующих причин при прохождении электронами области реверса. Эта проблема заслуживает отдельного изучения.
Литература:
1. Царев В. А., Спиридонов Р. В. Магнитные фокусирующие системы электровакуумных микроволновых приборов О-типа: учебное пособие. Саратов: изд-во «Новый ветер», 2010. 352 с.
2. Мельников Ю. А. Постоянные магниты электровакуумных СВЧ приборов. Изд-во «Советское радио», 1967. 183 с.
3. Кожанова Е. Р., Захаров А. А. Применение модернизированной вейвлет-функции «Французская шляпа» для аппроксимации продольного распределения магнитного поля в магнитных реверсивных фокусирующих системах // Молодой ученый. 2012. № 9. С. 25–29.
4. Кожанова Е. Р., Захаров А. А., Ткаченко И. М. Применение вейвлет-функций Гаусса второго порядка для аппроксимации продольного распределения магнитного поля различных видов МПФС // Актуальные проблемы электронного приборостроения АПЭП — 2012: Материалы 10-й юбилейной международ. научно-технич. конференции (19–20 сентября 2012, Саратов). Саратов, 2010. С. 446–451.

