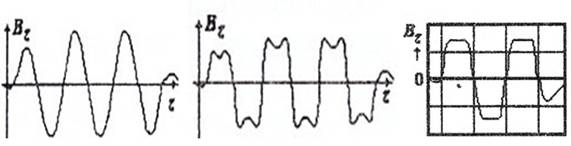
Известно, что для обеспечения фокусировки электронного потока в лампах бегущей волны (ЛБВ) применяются магнитные периодические фокусирующие системы (МПФС) различных видов [1]:
1) моногармонические МПФС (рис. 1а);
2) полигармонические МПФС (рис. 1б);
3) реверсивные МРФС (рис. 1в).
а) б) в)
Рис. 1. Продольное распределение магнитного поля в магнитных периодических фокусирующих системах (МПФС)
Возможность применения вейвлет-функций как аппроксимирующих функций для моделирования продольного распределения магнитного поля различных видов магнитных периодических фокусирующих систем (МПФС) рассмотрены в [1–3] и базируется на их графическом сходстве.
Моделирование всех видов МПФС, в том числе и полигармонических МПФС, разделено два основных этапа (рис. 2) [3]:
- моделирование продольного распределения магнитного поля ячейки МПФС (отдельного магнита);
- моделирование продольного распределения магнитного поля МПФС, которое реализуется с использованием реального механизма формирования распределения [4].
Для моделирования продольного распределения магнитного поля ячейки (отдельного магнита) полигармонических МПФС предложен подход, основанный на суммировании однополярных вейвлет-функций Гаусса второго порядка [1].
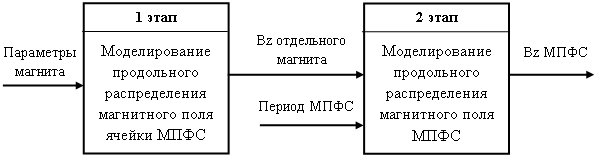
Рис. 2. Два этапа моделирования продольного распределения магнитного поля всех видов МПФС
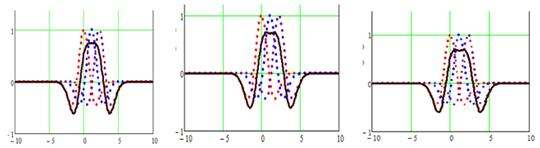
Рассмотрим формирование суммирующего распределения ячейки полигармонических МПФС, полученное суммированием двух (рис. 3а-в), трех (рис. 3г-е) и четырех (рис. 3ж-з) вейвлет-функций Гаусса второго порядка со сдвигом на величину S [1].
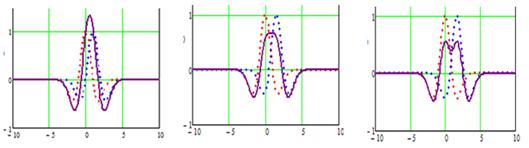
а) S=1.1 б) S=1.5 в) S=1.7
г) S=1.12 д) S=1.14 е) S=1.15
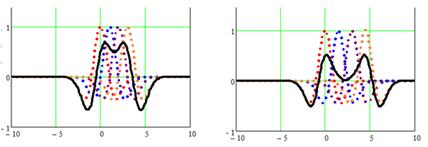
ж) S=1.01 з) S=1.5
Рис. 3. Суммирующее распределение ячейки (сплошная линия) из двух (а-в), трех (г-е) и четырех (ж-з) вейвлет-функций Гаусса второго порядка с различными значениями сдвига S
Из полученных суммирующих распределений ячеек (рис. 3) создаются распределение обратной полярности, чтобы образовать суммирующее распределение полигармонического МПФС. Для этого необходимо суммирующие распределения ячеек разной полярности сложить с учетом реального механизма формирования продольного распределения магнитного поля МПФС [5], сдвигая центры распределений ячеек на период МПФС [1]:
ТМПФС = S + 31/2 (1)
где S — сдвиг относительно центров двух соседних функций, 31/2 — абсцисса точки минимума функции.
Получим суммирующее распределение, по данной методике (рис. 4).
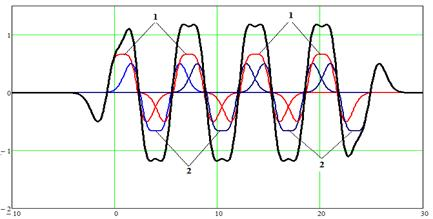
Рис. 4. Суммирующее распределение (сплошная линия) полигармонической МПФС из восьми суммирующих распределений: 1 — распределение (рис. 3а), 2 — обратное распределение
Составим алгоритм для моделирования продольного распределения магнитного поля полигармонической МПФС (рис. 5).
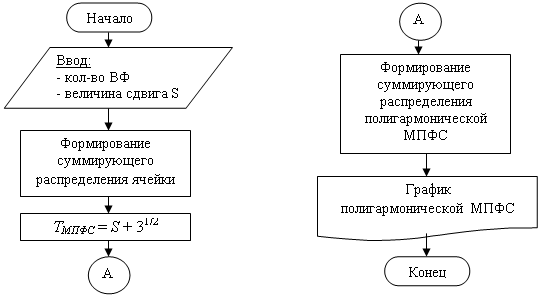 |
Рис. 5. Алгоритм моделирования продольного распределения магнитного поля полигармонической МПФС
На рис. 6 представлен листинг программы, позволяющий моделировать продольное распределение магнитного поля полигармонической МПФС в два этапа (см. рис. 2).
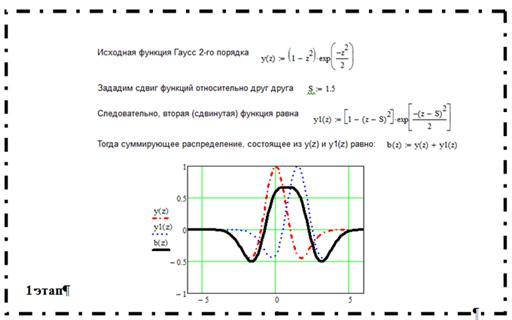
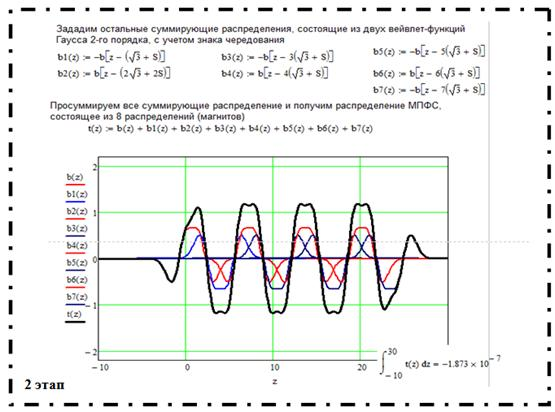
Рис. 6. Листинг программы моделирования продольного распределения магнитного поля полигармонической МПФС в среде MATHCAD
В дальнейшем планируется разработать пользовательское приложение, которое позволило бы моделировать продольное распределение магнитного поля различных видов МПФС с привязкой к параметрам магнитов, из которых состоит МПФС.
Литература:
1. Кожанова Е. Р., Захаров А. А., Ткаченко И. М. Применение вейвлет-функций Гаусса второго порядка для аппроксимации продольного распределения магнитного поля различных видов МПФС // Актуальные проблемы электронного приборостроения АПЭП — 2012: Материалы 10-й юбилейной международ. научно-технич. конференции (19–20 сентября 2012, Саратов). Саратов, 2010. С. 446–451.
2. Кожанова Е. Р., Захаров А. А. Применение модернизированной вейвлет-функции «Французская шляпа» для аппроксимации продольного распределения магнитного поля в магнитных реверсивных фокусирующих системах // Молодой ученый. 2012. № 9. С. 25–29.
3. Кожанова Е. Р., Захаров А. А., Ткаченко И. М. Возможность применение вейвлет-функции Гаусса первого порядка для моделирования магнитного поля реверсивных магнитных периодических систем // Молодой ученый. 2014. № 2. С. 149–152.
4. Кожанова Е. Р. Программа для моделирования продольного распределения магнитного поля магнитной реверсивной фокусирующей системы в среде MATHCAD // Новый университет. Серия: Технические науки. 2014. № 1. С.20–24.
5. Кожанова Е. Р., Захаров А. А. Формирование распределения суммирующих вейвлет-функций для моделирования продольного распределения магнитного поля магнитных периодических фокусирующих систем // Вестник Саратовского государственного технического университета. 2011. Т.4., № 1. С. 83–88.

