В статье построена сопряженная спектральная задача и условия биортогональности для вязкоупругой пластинки с переменной толщиной. Сформулирована спектральная задача, описывающая распространение изгибных плоских волн в волноводе. Численные решения спектральных задач проводились на ЭВМ программным комплексом, основанным на методе ортогональной прогонки С. К. Годунова в сочетании с методом Мюллера.
Рассматриваем вязкоупругий волновод в виде бесконечной вдоль оси х1 переменной толщины. Вязко упругие свойства материала учитиваются с помощю зависимости Больцмана — Вальтера [1]. Основные соотношения классической теории пластин переменной толщины можно получить на основе принципа возможных перемещений [2], в соответствии с гипотезами Кирхгоффа — Лява [3]. Пренебрегая членами, учитывающими инерцию вращения нормали к срединной плоскости, будем иметь следующее вариационное равенство:
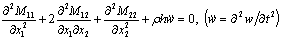, (1)
с естественными граничными условьями
; 
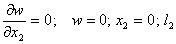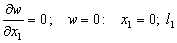. (2)
Для этого строится спектральная задача введя следующую замену переменных
; 
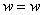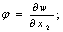
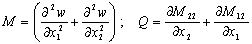(3)
Подставляя (3) в (1) получим систему интегро-дифференциальных уравнения в частных производных, разреженную относительно первых производных по х2. Рассмотрим бесконечную вдоль оси х1 полосу с произвольным законом изменения толщины h=h(x2). Будем искать решение задачи (1)-(3) в виде
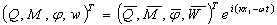(4)
описывающие гармонические плоские волны, распространяющиеся вдоль оси х1. Где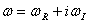 
- комплексная собственная частота; к- волновое число; 
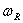-действительная часть комплексной частоты; 
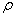-плотность. Подставляя систему интегро-дифференциальных уравнения в частных производных в (1), получим дифференциальные уравнения первого порядка, разрешенную относительно производных:
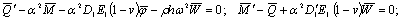
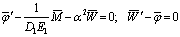, (5)
с граничными условиями на торцах полосы х2=0, l2, одного из двух типов
а. шарнирное опирание: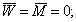 
б. скользящий зажим: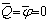 
, (6)
где 
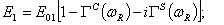
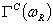и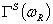 
-синус и косинус Фурье образы.
Таким образом, сформулирована спектральная задача (5) по параметру a2, описывающая распространение изгибных плоских волн в волноводе, выполненном в виде полосы с произвольным законом изменения толщины по координате х2. Покажем, что в случае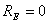 
спектральный параметр a2 принимает только действительные значения.
Пусть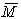 
и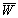 
некоторые собственные функции системы (5)-(6), возможно комплексные значения. Умножим систему уравнений (5) на 
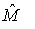и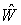 
комплексно сопряженные к 
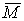и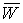 
функции. Тождественно преобразовав первое уравнение, проинтегрируем полученные равенства по х2 и составим следующую линейную комбинацию
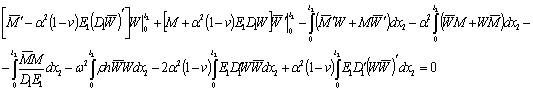(7)
Легко убедиться, что вне интегральных членов равенства (7) обращаются в нуль, при любой комбинации граничных условий (6). Показано, что при 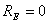в случае упругой пластинки квадрат собственного волнового числа для бесконечной полосы переменной толщины действителен при любой комбинации граничных условий (6). Если учитывается реологические свойства материала пластынки, то 
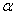становится комплексным. Полученная спектральная задача (5)-(6) не является самосопряженной. Построим для нее сопряженную задачу, используя для этого формулу Лагранжа [3]
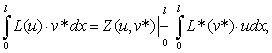где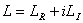 
и L* — прямой и сопряженный линейные дифференциальные операторы; 
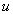и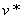 
— произвольные решения соответствующих краевых задач. В качестве примера рассмотрим стационарную задачу для полу бесконечной полосы переменной толщины. Рассмотрим полу бесконечный вдоль оси x1 полосу переменного сечения, на торце которой
(x1 =0) заданы гармонические по времени воздействия одного из двух типов:
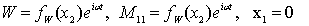
Численные решения спектральных задач проводилось на ЭВМ программным комплексом, основанным на методе ортогональной прогонки С. К. Годунова [1] в сочетании с методом Мюллера. Основной анализ проводится для безразмерных переменных, в которых плотность материала r, половина ширины волновода l2,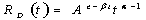 
, мгновенный модуль упругости Е приняты равными единице. Анализ полученных данных показывает, что область применимости теории Кирхгоффа — Лява к пластине постоянной толщины ограничена диапазоном низких частот. Например, для первой моды (h=0) диапазон применения теории 
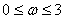из-за неограниченного роста фазовой скорости, для больших частот 
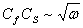. Рассмотрим сначала волновод с линейным законом изменения толщины. На основе полученных результатов выявлено, что в отличие от полосы постоянного сечения в случае клиновидного волновода с малым углом в основании клина a существует конечный предел фазовой скорости распространения моды, причем
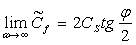
где СS — скорость волны сдвига, что совпадает с результатами исследований [5] и др.
Таким образом, показано, что теория Кирхгоффа-Лява позволяет получить волны, распространяющиеся в клиновидном волноводе с достаточно малым углом при основании клина скоростями, меньшими скорости волны сдвига и отличными от скорости волны Релея. Кроме того, эти волны, начиная некоторой частоты, распространяются без дисперсии.
Литература:
1. Бозоров М. Б., Сафаров И. И., Шокин Ю. И. Численное моделирование колебаний диссипативно однородных и неоднородных механических систем. СО РАН, Новосибирск, 1996.- 188с.
2. Гахов Ф. Д. Краевые задачи. М.: Физматгиз, 1963. -639 с.
3. Неймарк М. А. Линейные дифференциальные операторы. М.: Наука, 1969.- 526 с.
4. Марчук Г. И. Методы вычислительной математики. М.: Наука, 1977.- 456 с.
5. Гринченко В. Т., Мелешко В. В. Гармонические колебания и волны в упругих телах, К.: Наука думка, 1981, -283с.
