В статье рассматриваются методики решения задач воздействия нестационарных волн на N-слоистых цилиндрических телах (оболочках), находящихся в безграничной линейно-упругой среде, а также их алгоритмы. Построена замкнутая система дифференциальных уравнений в соответствующих начальных и граничных условиях. Полученные аналитические результаты имеют теоретическое и прикладное значение. Разработанная методика носит универсальный характер, она справедлива при любых реологических свойствах сред.
The methods for solving the problems of the action of nonstationary waves on N-layered cylindrical bodies (shells) in an unbounded linearly elastic medium and their algorithms are considered in the article. A closed system of differential equations is constructed in the corresponding initial and boundary conditions. The obtained analytical results have theoretical and applied significance. The developed methodology is universal, it is valid for any rheological properties of media.
Введение. Вслучае достаточно протяженной полости и воздействия, направленного перпендикулярно продольной оси, окружающая полость среды и обделки находятся в условиях плоской деформации, а задачи определения напряженного состояния массива и обделок сводятся к плоской задаче динамической теории упругости [1,2,3,4]. В работах [5,6,7] решены задачи о напряженно-деформируемом состоянии цилиндрических тел (оболочка), находящихся в безграничной линейно-упругой среде при распространении продольных и поперечных волн. В отличие от других работ, в настоящей работе уделяется внимание разработке методике решения и алгоритму задачи взаимодействия нестационарных волн в слоистых цилиндрических телах. Данная методика справедлива при любых реологических свойствах сред.
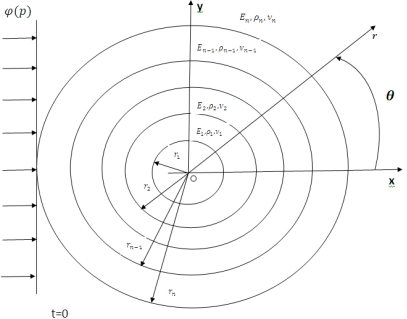
Рис.1. Расчётная схема слоистых цилиндрических тел в упругой среде
Постановка задачи. На N-слойный цилиндр падают нестационарные волны напряжения 
и 
, фронт которых параллелен продольной оси цилиндра [1] (рис.1). Требуется определить динамическое напряженно-деформированное состояние цилиндра и окружающей его среды, вызванное падающим импульсом напряжения. Предположим, что время t отсчитывается с момента, когда падающий импульс коснется поверхности внешнего (N-1)-го цилиндра в точке 
. До этого момента сохраняется покой. В соответствии с изложенным, задача отыскания поля дифрагированных волн и напряженно-деформированного состояния, вызванного падающим импульсом, может быть записана уравнениями [1]
(1)
где
— амплитуда падающих волн; 
- единичная функция Хевисайда. Сначала найдём решение для плоской ступени частной волны. Тензор напряжения в общем виде:
где 
- напряжение при падающих волнах, 
- напряжение отраженных волн.
В полярной системе координат, связанной с цилиндром, напряжение и смещение в падающей волне 
имеют вид:
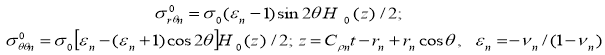
где Ho (z) –единичная функция Хевисайда; 
- напряжения на фронте волны, распространяющейся в направлении х1; rj — радиус слоистых тел (j=1,….n); Срj- скорость волны расширения, 
- коэффициенты Пуассона, 
-плотности сред. В отсутствие статических массовых сил, вектор смещений 
в упругой среде определяется уравнением
(2)
Вектор смещений (
) выражается через скалярный (
) и векторный (
) потенциалы [2]
,
а уравнение (2) принимает вид
, 
. (3).
где 
– дифференциальные операторы в цилиндрических координатах.
На бесконечности r → ∞ потенциалы продольных и поперечных волн при 
удовлетворят условию излучения Зоммерфельда [1]:
, (4)
.
На контакте двух тел r = rj выполняется равенство смещений и напряжений (условие жесткого контакта)
, (5)
а на свободной поверхности (r = r1):
(6)
Задача решается при следующих начальных условиях:
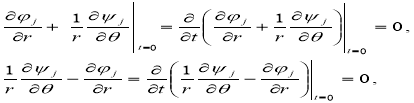(7)
Поле напряжений, вызванных усилиями (1), удовлетворяет волновому уравнению (3), т. е. ему удовлетворяет каждый цилиндрический слой. Для решения сформулированной выше задачи применим по времени t-интегральное преобразование Фурье
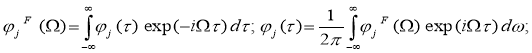(8)
где 
-параметр интегрального преобразования Фурье; 
изображение преобразования Фурье функций 
и 
соответственно. Использовав нулевые начальные условия (7), получим изображенную задачу (3). Тогда решение уравнений изображенной задачи будет иметь вид
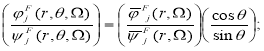(9)
Здесь 
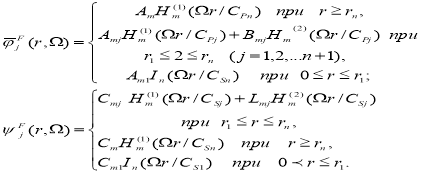
Коэффициенты
определяются из граничных условий (4)-(6). Граничные условия с учетом падающих волн (1) примут вид:
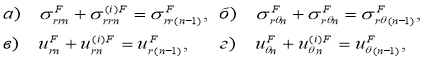(11)
где
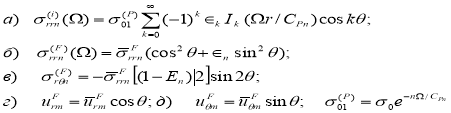(12)
Подставив (9) и (10) в граничные условия (4),(5) и (6), получим систему комплексных алгебраических уравнений с (4n + 3) неизвестными в виде
(13)
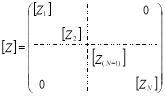
где Z-блочная матрица;
матрица размерности 4x4, элементы которой суть функции Бесселя и Ханкеля m-го порядка первого и второго рода; {g}-вектор-столбцы неизвестных коэффициентов; {P}-{0,0.....0,Р1n, Р2n, Ргn, Р4n }T-вектор-столбцы, характеризуюшие падающие нагрузки. Пусть ступенчатые волны взаимодействуют с цилиндрическим отверстием при r = r1 и отверстием свободного от напряжения (
Единственньм напряжением, которое не обращается в нуль при r = r1, является кольцевое напряжение 
. Применив преобразование Фурье к уравнению движения и граничньм условиям [9], получим выражение для кольцевых напряжений при
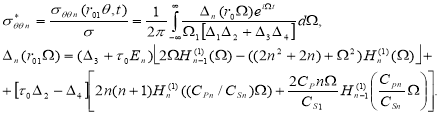(14)
Выражение 
приведено в работе [10]. Несобственный интеграл (14) решается численно по разработанным алгоритмам [10]. Практически вычисление (4) на ЭВМ можно провести следующим образом. Поскольку численное интегрирование в бесконечных пределах немыслимо, то интеграл (14) заменяется на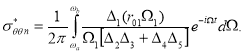 
(15)
Значения пределов интегрирования 
подбираются в зависимости от вида падающего импульса. Численные значения спектральной плотности 
из (12) конечного падающего импульса лишь в небольшом диапазоне частоты 
существенно отличаются от нуля. Пределы интегрирования следует подбирать в соответствии с этим диапазоном и с учетом требуемой точности. При этом остаётся открытым вопрос о том, какую погрешность внесет пренебрежение вкладом интегралов типа (14) в пределах интегрирования от — 
до 
и от 
до 
. Численное суммирование бесконечной суммы (12), разумеется, также невозможно. Однако в [10] показано, что при достаточно больших n (n-порядок функций Бесселя и Ханкеля) можно построить асиптотическое представление общего члена этой суммы. В результате становятся возможными либо оценка погрешности перехода от бесконечной суммы к конечной, либо приближенное суммирование бесконечной суммы. Ввиду вышесказанного сохраним в (12) бесконечную сумму. Расчет по рассматриваемому методу сводится к построению двух алгоритмов вычисления: коэффициентов 
(13) и интеграла (15). Первый и второй алгоритм не зависят от вида математической модели объекта. При вычислении интеграла (15) по методу Ромберга приходится многократно вычислять подинтегральную функцию. Обратное преобразование Фурье для некоторого изображения, оригинал которого заранее известен, показало, что при длине шага интегрирования 0,01, погрешность процедуры не превышает 0,3–0,5%. В качестве примера рассмотрим дифракции нестационарных волн на цилиндрическом теле. Пусть внутренная граница (
) свободна от напряжения, а на контакте с окружаюшей средой вьполняется условие равенства перемещений и напряжений (5) [1,2,4,10]. После преобразования Фурье получим цилиндрические уравнения Бесселя, решение которых выражается (9) и (10). В нашей задаче будет шесть произвольных постоянных, которые определяются из граничных условий (6) и (11). Результаты расчетов приведены при 
(
). При интегрировании предела приняты следующие значения 
. Изменение окружного напряжения 
в зависимости от 
показано на рис.2.
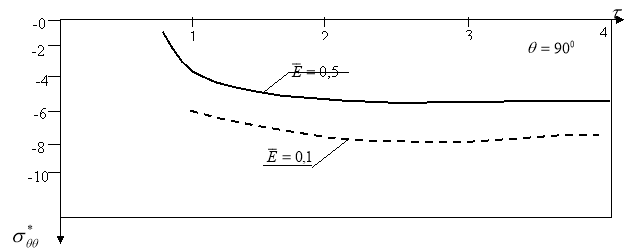
Рис. 2. Зависимость кольцевого напряжения цилиндрического слоя от времен 
Различие между напряжениями на внешней и внутренней поверхностях достигает
, а различие между напряжениями на серединной и внутренней поверхностях 
Выводы:
‒ сопоставление результатов для волн сдвига с продольными волнами показывает, что в продольных волнах возникает больше напряжение, чем волны сдвига,
‒ расчеты показывают, что при 
результаты данного исследования приближаются к точному статическому значению
. Видно, что максимальное напряжение и перемещения существенно зависят от 
и 
.
Литература:
- Гузь А. Н., Кубенко В. Д., Черевенко М. А. Дифракция упругих волн. «Наука», 1978. 308 с.
- Pao Y. H., Mow C. C. Diffraction of elastic waves and dynamic stress concentration. № 4, Grane, Russak, 1973 694 p.
- Datta S. K. Tensional waves in an infinite elastic solid containing a penny-shaped crack.-z. answer. Math. And Phys., 1970, 21, № 3, р.343–351
- Мубариков Я. Н., Сафаров И. И. О действии упругой волны на цилиндрическую оболочку. Изв.АнУзССР, серия технических наук, 1987. № 4. с. 34–40
- Сафаров И. И. Оценка сейсмонапряженного состояния подземных сооружений методики волновой динамики. Сборник «Сейсмодинамика заданий и сооружений» Ташкент, Фан. 1988.
- Сафаров И. И., Жумаев З. Ф. О разрушении тоннеля при сильных движениях земли. Международная конференция по сейсмостойкому строительству. С-Петербург, 2000, с. 71–78
- Рашидов Т. Р., Сафаров И. И. и др. О двух основных методах изучения сейсмонапряженного состояния подземных сооружений при действии сейсмических волн. Ташкент: ДАН. № 6, 1989. С. 13–17.
