В статье рассматривается учет вкладов высших порядков теории возмущений в сечение рождения тяжелых кварков в рамках k T -факторизационного подхода. Изучение b и c струй позволяет получить информацию о функциях распределения партонов, которые описывают вероятность нахождения кварков (в частности, тяжелых) и глюонов внутри протона или ядра. Это важно для понимания процессов, происходящих внутри протона и ядра при высоких энергиях, таких как столкновения в ускорителях. Кроме того, изучение струй тяжелых кварков позволяет проверить теоретические модели и предсказания, связанные с функциями распределения партонов. Это важно для дальнейшего развития науки и технологий, связанных с физикой высоких энергий.
1 Введение
В работах в данной области, таких как [1, 2] были представлены расчеты сечений рождения D -мезонов и струй тяжелых кварков при энергиях коллайдера Теватрон в рамках k t -факторизации. В работах [3, 4] были проведены расчеты для b -струй, а также D и B -мезонов. К результатам работ [5, 6] мы должны относиться с определенной осторожностью. Для четкого заключения о неприменимости распределений КМР с условием углового упорядочения (по крайней мере в 5FS) видится необходимым рассмотрение лидирующего подпроцесса Q ∗ g ∗ → Q , к которому подпроцессы 2 → 2 добавляются как поправки высоких порядков, причем с использованием определенных процедур вычитания, устраняющих двойной счет. Данная работа является подготовительной для подобной работы.
Итак, целью нашей работы является исследование процесса рождения тяжелых кварков в k T факторизационном подходе при энергиях LHC, основываясь на процессе 2 → 1 в 5FS. Для этого мы независимо вычислим внемассовый матричный элемент g ∗ Q ∗ → Q и получим сечения рождения D мезонов и b -струй в различных кинематических областях с помощью TMD функций распределений КМР. Полученные результаты дадут нам возможность сделать выводы о применимости этих распределений к процессам с рождением тяжелых кварков. Мы также опишем способ, с помощью которого для таких процессов можно учесть вклады высоких порядков теории возмущений, связанные с дополнительными испусканиями партонов, избегая при этом двойного счета. Таким образом, наша работа имеет большое значение для понимания и описания функций распределения и может быть использована в дальнейших исследованиях в этой области.
2 Теория
2.1Неинтегрированные функции распределения в подходе КМР
В рамках рассмотрения процесса с использованием KMR-подхода мы предполагаем, что условие сильного упорядочивания в уравнениях ДГЛАП можно ослабить на последнем шаге партонной эволюции:
k 1 T ≪ k 2 T ≪ ... ≪ k nT ∼ µ (1)
Данное действие позволяет учесть большую часть логарифмических членов вида:
α s ( α s ln µ 2 ) n −1 , хотя в обычном коллинеарном приближении идет учет членов степени n . Поскольку поперечный импульс партона, входящего во взаимодействие, теперь имеет порядок величины масштаба жесткого подпроцесса, им нельзя пренебречь, и функции распределения начинают зависеть от поперечного испульса k T .
Исходя из выше перечисленных условий, мы можем переписать уравнения ДГЛАП на масштаб k t :
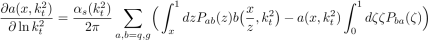
где P — нерегуляризованные функции расщепления ДГЛАП, а ζ введена во второй интеграл, чтобы избежать двойного счета.
Используя форм-фактор Судакова можно просуммировать все петлевые вклады.
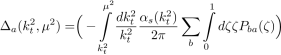
Данное выражение дает вероятность эволюции от масштаба k t до µ без испускания партона. После некоторых математических выкладок, окончательно получим:
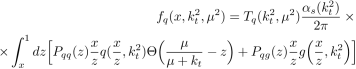
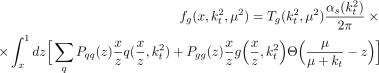
где P qq ( z ) ,P qg ( z ) ,P gq ( z )—функции расщепления в уравнении ДГЛАП в лидирующем порядке, q ( x,µ 2 ) и g ( x,µ 2 )—коллинеарные кварковые и глюонные распределения соответственно, удовлетворяющие уравнению ДГЛАП, T q ,T g —кварковые и глюонные форм-факторы Судакова:
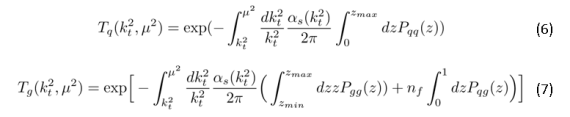
На рис. 1 наглядно видно, что PB-распределения спадают с ростом k T гораздо быстрее, чем в случае подхода KMR: при значениях, превышающих масштаб, PB-распределения становятся пренебрежительно малыми. Отличительное свойство распределений KMR, полученных с использованием условия углового упорядочения состоит в том, что их вклад существенен в области k T > µ . Утверждается, что за счет этой области происходит учет более высоких логарифмических поправок.
В качестве входных коллинеарных распределений для наших вычислений мы использовали функции MSTW2008LO [7].
2.2 Неинтегрированные функции распределения в подходе Parton branching (PB)
Основная идея данного метода [8, 9] заключается в том, что мы вводим в уравнение эволюции ДГЛАП параметр разрешения z M , который позволяет разделить процессы на разрешимые и неразрешимые. Описание процессов в данном явлении будет производиться с помощью функции вероятности бренчинга
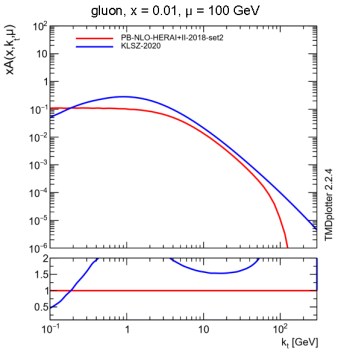
Рис. 1. График сравнения функций распределения: красным показана PB-функция распределения, синим — KMR-функция распределения
P ba R ( α s ,z M ) и форм-факторами Судакова. Сохраняя в ходе решения уравнений ДГЛАП методом Монте-Карло в каждом бренчинге поперечный импульс, можно получить в итоге неинтегированные TMD функции распределения партонов.
Уравнение эволюции для TMD PB-распределения имеет вид:
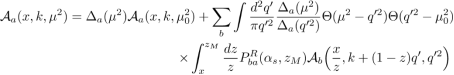
где ∆( µ 2 ) — форма-фактор Судакова, а P ba R — регуляризованные функции расщепления. Учитывая, что
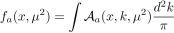
из (8) можно получить стандартное уравнение ДГЛАП:
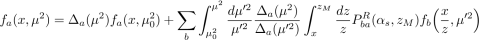
Данные партонные плотности хорошо описывают экспериментальные данные в широком диапазоне x и µ 2 . На рис.(1) приведено сравнение функций распределения PB и KMR (в имплементации KLSZ2020 [10]). На рис. 1 наглядно видно, что PB-распределения спадают с ростом k T гораздо быстрее, чем в случае подхода KMR: при значениях, превышающих масштаб, PB-распределения становятся пренебрежительно малыми. Отметим, что подобное поведение наблюдается также и для распределений, полученных решением уравнения КЧФМ.
2.3 Расчет партонных сечений
2.3.1 Подпроцесс g ∗ q ∗ → q
В низшем порядке теории возмущений процесс рождения тяжелого кварка в 5FS будет описанна данным матричным элементом:
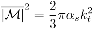
что в точности совпадает с результатами работ [1, 2]. и соответствующее данному процессу сечение:
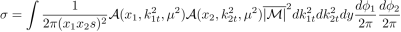
2.3.2 Подпроцессы высших порядков g ∗ g ∗ → qq ¯ и g ∗ q ∗ → gq
Данные подпроцессы можно описать представленными диаграмами Фейнмана, изображенных на рис. 2 и 3.
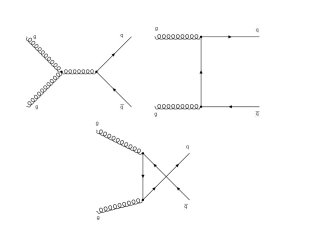
Рис. 2. Диаграмма Фейнмана для рождения пары кварк-антикварк в процессе взаимодействия двух глюонов
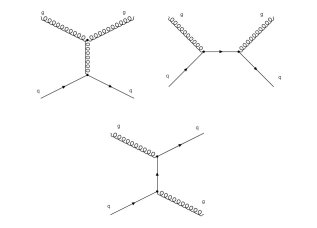
Рис. 3. Диаграмма Фейнмана для рождений пары глюон-кварк в процессе взаимодействия глюонкварковой пары (комптоновское рассеяние в КХД)
Подпроцесс g ∗ g ∗ → qq ¯ был расчитан в работе [11]. Можно привести формулу для сечения данного подпроцесса:
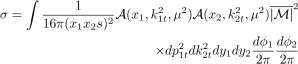
Подпроцесс g ∗ q ∗ → gq был учтен с помошью Монте-Карло генератора KaTie [12].
В этом порядке теории возмущений есть еще два подпроцесса: q ∗ q ¯ ∗ → QQ ¯ и Q ∗ q ∗ → Qq . Эти процессы включают в себя только кварки в начальном состоянии. Кварковые плотности при малых значениях переменной x значительно меньше, чем глюонные плотности. Таким образом эти вклады в рассматриваемой кинематической области будут малы, поэтому в данной работе мы ими пренебрегаем.
3 Численные результаты
В данной работе для вычисления полных и дифференциальных сечений была написана программа на языке програмирования C++. Расчет многомерных интегралов был проведен методом Монте-Карло [13] с помощью функции VEGAS [14].
В наших расчетах масштаб ренормализации и масштаб факторизации были равны: µ 2 R = µ 2 F = ( p 2 t + m 2 B ). Для того чтобы изучить теоретическую неопределенность, которая связанна с выбором µ R и µ F была проведена процедура вариации масштаба, а именно от 1 / 2 µ R до 2 µ R . Также в исследовании было проведено вычисление сечений при 0 массе кварков в процессе 2 → 1, а для подпроцессов 2 → 2 мы провели исследование: как на сечение рождение тяжелых кварков влияет масса кварка, т.е. были произведены вычисления при m = 0 и m = m q . Для α s ( µ 2 R ) мы использовали стандартное выражение при N F = 5 и Λ QCD = 200 МэВ. Также было проведено сравнение с данными CMS (для b -струй) [15] и с данными колаборации ALICE (для образования D 0 -мезона) [16].
3.1Рождение b -струй при энергиях LHC
На рис. 4, 5 показаны дифференциальные сечения инклюзивного рождения b -струй, рассчитанные нами в разных подходах: с помощью функций распределения КМР и PB в сравнении с данными, полученными на LHC коллаборацией CMS. Рассматривались сечения, полученные при энергии S = 7000 ГэВ, на показанных графиках шел учет кинематической области | y | < 0 . 5. Видно, что экспериментальные данные CMS не могут быть описаны обоими наборами неинтегрированных функций распределения в LO 5FS. Причем если для случая PB распределений можно говорить о возможности улучшения описания при учете более высоких порядков теории возмущений, то данные, полученные с помощью функций КМР значительно превышают экспериментальные результаты. Таким образом, мы подтверждаем вывод, сделанный в [5, 6], исходя из рассмотрения подпроцесса q ∗ g ∗ → qg : функции распределения КМР с учетом углового упорядочения для b -кварка неприменимы в 5FS.
Также мы рассмотрели тот же процесс в 4FS с помощью подпроцесса главного порядка g ∗ g ∗ → qq ¯ (рис. 5) в подходе КМР. На рис. 5 изображена фиолетовая линия, соответствующая расчету в 5FS, а коричневая линия показывает результат, полученный в 4FS. В этом случае все три кривые находятся в хорошем согласии друг с другом, за исключением области малых p T , где имеют значение массовые эффекты. При этом подпроцесс 2 → 1 с хорошей точностью воспроизводит результат подпроцесса 2 → 2 во всей области, что говорит о том, что плотность распределения тяжелого кварка в подходе PB в большей степени обусловлена глюонным расщеплением.
![Дифференциальные сечения рождения b-струи как функция поперечного импульса b-струи в области |y| < 0.5, полученные с помощью КМР-распределений (фиолетовый) и PB-распределений (коричневый) в подпроцессе g∗q∗ → q. Экспериментальные данные коллаборации CMS [15]](https://articles-static-cdn.moluch.org/articles/j/104376/images/104376.015.png)
Рис. 4. Дифференциальные сечения рождения b -струи как функция поперечного импульса b -струи в области | y | < 0 . 5, полученные с помощью КМР-распределений (фиолетовый) и PB-распределений (коричневый) в подпроцессе g ∗ q ∗ → q . Экспериментальные данные коллаборации CMS [15]
![Дифференциальные сечения рождения b-струи как функция поперечного импульса b-струи в области |y| < 0.5, полученные с помощью КМР-распределений в подпроцессе g∗q∗ → q (фиолетовый), g∗g∗ → qq¯ при массе b-кварка 4.7 ГэВ (коричневый) и при массе b-кварка равной 0 ГэВ(красный). Экспериментальные данные коллаборации CMS [15].](https://articles-static-cdn.moluch.org/articles/j/104376/images/104376.016.png)
Рис. 5. Дифференциальные сечения рождения b -струи как функция поперечного импульса b -струи в области | y | < 0 . 5, полученные с помощью КМР-распределений в подпроцессе g ∗ q ∗ → q (фиолетовый), g ∗ g ∗ → qq ¯ при массе b -кварка 4.7 ГэВ (коричневый) и при массе b -кварка равной 0 ГэВ(красный). Экспериментальные данные коллаборации CMS [15].
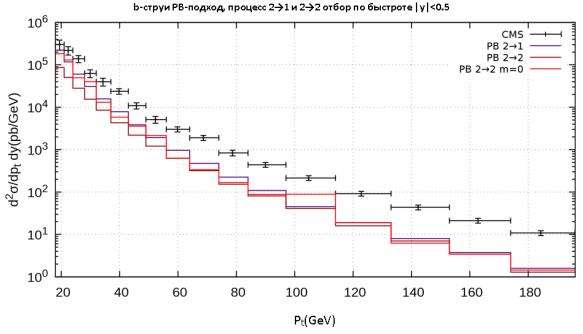
Рис. 6. Дифференциальные сечения рождения b -струи как функция поперечного импульса b -струи в области | y | < 0 . 5, полученные с помощью PB-распределений. Обозначения те же, что и на рис. 5
3.2 Сечение рождения D 0 мезона при энергиях LHC
В работах коллаборации ALICE [16] получены данные для сечений инклюзивного рождения D 0 -мезонов. В данном эксперименте рассматривались протон-протонные столкновения при энергии системы центра масс S = 7000 ГэВ. Также было проверено, как в рамках k t -факторизационного подхода будут описаны экспериментальные данные. На рис. 7 представлено дифференциальное сечение инклюзивного рождения D 0 -мезонов из процесса адронизации очарованных кварков. В ходе вычислений мы использовали, помимо расчетов матричных элементов, функцию фрагментации, которая характеризует сечение рождения D 0 мезона, исходя из импульсов и сечений c -кварка. Фрагментация была смоделирована с помощью функций Петерсона [17]:
D ( z ) = z (1 . 0 − z ) 2 / ((1 . 0 − z ) 2 + εz ) 2 , (14)
где ε = 0 . 06. Обозначения аналогичны рис. 4. Интересно отметить, что в данном случае можно получить хорошее описание сечений с помощью функций КМР в подходе, основанном на подпроцессе g ∗ q ∗ → q , за исключением двух первых бинов, где большую роль играет масса c -кварка. Таким образом, можно сделать вывод, что проблематичное поведение функций КМР наиболее ярко проявляется именно для b -кварков.
![: Дифференциальное сечение рождения D0-мезона как функция поперечного импульса D0мезона. Обозначения гистограмм те же, что и на рис. 4. Экспериментальные данные коллаборации ALICE [16]](https://articles-static-cdn.moluch.org/articles/j/104376/images/104376.018.png)
Рис. 7: Дифференциальное сечение рождения D 0 -мезона как функция поперечного импульса D 0 мезона. Обозначения гистограмм те же, что и на рис. 4. Экспериментальные данные коллаборации ALICE [16]
3.3 Учет вкладов высших порядков теории возмущений в сечение рождения тяжелых кварков
В данном разделе будет предложен метод, с помощью которого мы сможем учесть в k T -факторизации вклады более высоких порядков, для процессов рождения тяжелых кварков, связанные с дополнительными испусканиями партонов. Предлагаемый способ позволяет при таком учете избежать двойного счета. При счете подпроцесса g ∗ q ∗ → q если мы напрямую будем учитывать вклад высоких порядков, то столкнемся с проблемой, а именно переоценкой действительного значения сечения.
σ sum = σLO + σNLO + ... (15)
где σ NLO и σ LO являются сечения от соответствующих порядков. Такая переоценка связана с тем, что часть вкладов, связанных с испусканием партонов автоматически учитывается в k T -факторизационном подходе с помощью неинтегрированных функций распределения партонов. Таким образом, правильная формула в NLO включает в себя некоторое компенсирующее слагаемое:
σ sum = σLO + σNLO − σ sub(16)
Рассмотрим процесс рождения b -кварка в подходе PB. Для оценки σ sub воспользуемся методом, предложенным в работах [18, 19].
σ sum = σLO − σLO ( kT < kT cut) + σNLO − σNLO ( pT > kT cut) . (17)
Для того, что бы оценить k T cut нами были проведены расчеты dσ/dk T —для случая g ∗ q ∗ → q и dσ/dp T — в случае g ∗ q ∗ → gq (рис. 8). Логично взять k T cut так, чтобы сумма этих сечений после вычитания (16) имела наиболее гладкий вид. Для этого возьмем k T cut в точке наибольшего сближения этих кривых.
Видно, что такое сближение достигается при k T cut ∼ 20 ГэВ.
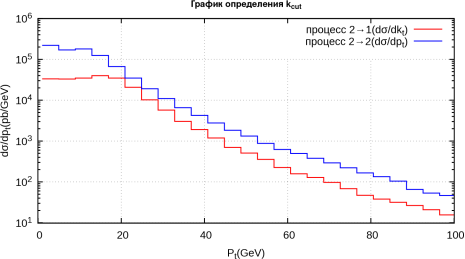
Рис. 8. Дифференциальные сечения рождения b -кварков, в PB-распределении, в процессах 2 → 1 (красный) и 2 → 2 (синий) для получения значения k T cut
На рис. 9 видно, что предложенный нами метод отлично описывает экспериментальные данные и дает высокую точность предсказания данных для будущих экспериментов. Наш метод позволяет более точно определять значения параметров, что очень важно для определения сечений процессов высоких энергий с учетом вкладов высших порядков.
![Дифференциальное сечение рождения b-кварков в PB-подходе. Синим показана линия, учитывающая вклады высших порядков, красным только первый порядок. Экспериментальные данные коллаборации CMS [15]](https://articles-static-cdn.moluch.org/articles/j/104376/images/104376.020.png)
Рис. 9. Дифференциальное сечение рождения b -кварков в PB-подходе. Синим показана линия, учитывающая вклады высших порядков, красным только первый порядок. Экспериментальные данные коллаборации CMS [15]
4 Заключение
В данной статье были рассмотрены процессы инклюзивного рождения b -струй и рождение D 0 -мезона в рамках k T -факторизационного подхода КХД при энергиях LHC. Формализм k T факторизационного подхода вытекает из уравнений эволюции БФКЛ или КЧФМ, что позволяет, в отличие от уравнения ДГЛАП, учесть вклад от больших логарифмов вида ln (1 /x )
В работе был вычислен внемассовый матричный элемент для подпроцесса g ∗ q ∗ → q с учетом массы кварка. Было показано, данные CMS для инклюзивного рождения b -струй хорошо описываются с помощью неинтегрированных функций распределения КМР в 4FS, в то время как результаты в 5FS дают значительную переоценку сечений во всей кинематической области. Таким образом мы подтверждаем сделанный ранее на основании другого расчета вывод о неприменимости подхода КМР для схемы с 5 активными кварковыми ароматами. В то же время результаты, полученные для рождения D 0 -мезонов, хорошо описывают экспериментальные данные.
При описании в PB-подходе мы столкнулись с меньшим сечением, чем указывается данными. В данной работе был представлен метод, как мы можем правильно описать имеющиеся данные, учитывая поправки от высших порядков теории возмущений. После применения нашего метода, мы смогли адекватно описать данный процесс и полученные нами результаты отлично описывают экспериментальные данные.
Литература:
- B. A. Kniehl, A. V. Shipilova, V. A. Saleev.//Phys.Rev.D79:034007,2009.
- B. A. Kniehl.V. A. Saleev and A. V. Shipilova.//Phys.Rev.D81:094010,2010.
- H. Jung, M. Kraemer, A. V. Lipatov, N. P. Zotov.//JHEP 1101:085,2011.
- H. Jung, M. Kraemer, A. V. Lipatov, N. P. Zotov.//Phys.Rev.D81:094010,2010.
- B. Guiot and A. van Hameren.//PhysRevD.104.094038.
- B. Guiot.// Phys. Rev. D 107, 014015.
- A. D. Martin, W. J. Stirling, R. S. Thorne, G. Watt.//Eur.Phys.J.C63:189–285,2009.
- F. Hautmann, H. Jung, A. Lelek, V. Radescu, R. Zlebcik.// JHEP 2018:070,(2018).
- F. Hautmann, H. Jung, A. Lelek, V. Radescu, R. Zlebcik.// Phys. Lett. B. 772:10(201.
- A. V. Kotikov, A. V. Lipatov, B. G. Shaikhatdenov, P. Zhang.//JHEP 2020:28(2020).
- H. Jung, M. Kraemer, A. V. Lipatov, N. P. Zotov.//JHEP 1101:085,(2011).
- A. van Hameren.// Comput.Phys.Commun. 224 (2018) 371–380.
- CMS collaboration.//JHEP 2012:84(2012).
- G.Peter Lepage.// J. Comput. Phys. 27, 192–203 (1978).
- The CMS collaboration.// JHEP04(2012)084.
- ALICE Collaboration.// Eur. Phys. J. C (2017) 77:550.
- C. Peterson, D. Schlatter, I. Schmitt, and P. M. Zerwas. //Phys.Rev.D27,105
- R. Maciula and A. Szczurek.//Phys.Rev.D100,054001(2019)
- A. V. Lipatov, H. Jung,M. A. Malyshev.//Phys.Rev.D101,034022(2020)

