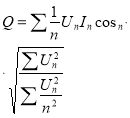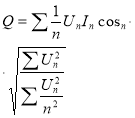Практическое применение вейвлет-преобразования для исследования нестационарных несинусоидальных сигналов и расчёта мощности



Вейвлет-преобразование в настоящее время имеет большую популярность для анализа нестационарных режимов в электроэнергетике. Так как оно решает те недостатки, которые присуще преобразованию Фурье.Преобразование Фурье даёт информацию о частотах исследуемого сигнала, но не даёт сведенья о локальных особенностях сигнала. Поэтому при использовании преобразования Фурье можно получать информацию либо во временной области, либо в частотной. Вейвлет-преобразование справляется с этой задачей.

Применение вейвлет-преобразования для расчёта реактивной мощности.

Существуют несколько видов вейвлет-преобразований: непрерывное, дискретное, пакетное, диадное.

Различные подходы применения дискретного вейвлет-преобразования при несинусоидальных режимах описаны в [1]. Дискретное ВП имеет логарифмическую шкалу частотных коридоров, что позволяет с успехом решать задачи по разложению исходного сигнала две компоненты: на основную частоту и высшие гармоники [2].

В литературе [3–5] представлено применение пакетного вейвлет-преобразования. Преимуществом пакетного вейвлет-преобразования служит возможность выделения различных полос частот в отдельные составляющие.

Методики определения реактивной мощности.

Существуют различные методики определения реактивной мощности. Возможно разделить все существующие методы на три группы:

1. спектральные методы;
2. интегральные методы;
3. энергопотоковые

В данной работе мы будем использовать методы определения мощности по Буденау, по Шарону, по Кастерсу-Муру, которые относятся к спектральным методам. А также методы определения мощности по Фризе и по Зарнецкому, относящиеся к энергопотоковым методам определения реактивной мощности.

Практическое применение вейвлет-преобразования для расчёта мощности.

Смоделируем нестационарный несинусоидальный режим в MATLAB.

Сигналы напряжения зададим выражениями

,

.

Частота Гц, Сопротивление Ом, индуктивность Гн.

Сигналы тока:

,

.

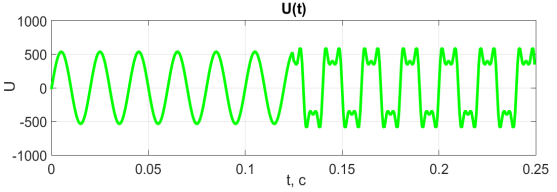
Покажем на рисунке 1 и 2 графическую интерпретацию заданных сигналов напряжения и тока, и также мгновенной мощности, которая получена путём перемножения сигналов тока и напряжения. Отметим, что на интервале времени содержится частота Гц, а на интервале времени содержатся частоты Гц, Гц, Гц.

а)

б)

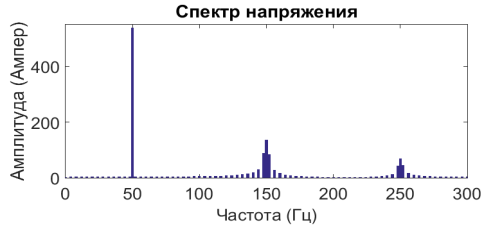
Рис. 1. а- Сигнал напряжения; б- Спектр напряжения

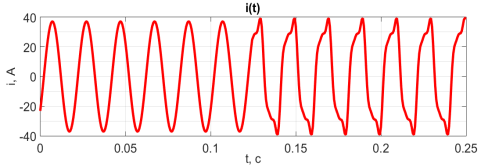
а)

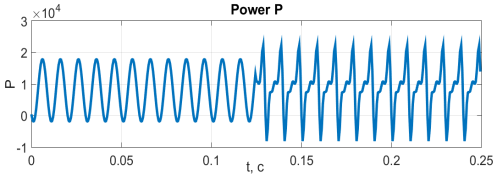
б)

Рис. 2. а- Ток; б- Мгновенная мощность нестационарного несинусоидального сигнала

В таблице 1 приведены действующие значения токов и напряжения, а также сравнение значений путём расчёта погрешности измерения.

Таблица 1

Сравнение точности вычисления действующих значений напряжений итоков различными типами вейвлетов

Величина	Расч. знач.	Расчет по вейвлет- коэффициентам				Погрешность,%
		Haar	db 10	db 24	db42
, А	26,311	23,258	26,339	26,312	26,311	0
, А	6,676	15,986	5,905	6,655	6,642	0,509
, А	2,117	9,809	3,364	2,169	2,211	4,441
, А	26,773	29,878	27,201	27,211	27,226	1,692
, А	380	379,392	379,302	380,217	380,209	0,055
, А	190	149,113	206,544	191,283	189,763	0,125
, А	95	154,315	59,359	90,584	93,614	1,459
, А	408,611	435,874	435,952	435,675	435,123	6,488

При сравнении значений видим, что наименьшая погрешность получилась при расчётах значений по вейвлет-коэффициентам db 42.

Рассчитаем реактивную мощность для данного случая, используя различные методики. При расчётах используем действующие значения токов и напряжений рассчитанных по классическим формулах, где интеграл заменён суммой. Сведём результаты расчётов в таблицу 2.

Таблица 2

Расчёт реактивной мощности, используя разные методики определения для нестационарного несинусоидального режима

	Название способов определения мощности	Формула	Реактивная мощность
			, вар	, вар	, вар	, вар
1	Классическая		6002,6	1242	199,481	7444,1
2	Мощность по Буденау		6002,6	1159,3	194,374	7356,3
3	Мощность по Фризе		9994,3	1268,4	201,152	10936
4	Мощность по Шарону		6002,6	1159,3	194,374	6969,7
5	Мощность по Кастерсу-Муру		6002,6	1159,3	194,374	6427,9
6	Мощность по Зарнецкому		6002,6	1159,3	194,374	6969,7

Далее рассчитаем аналогичным способом реактивную мощность. Но в расчётах используем действующие значения токов и напряжений, полученные с помощью вейвлет-коэффициентов Добеши 42 порядка. Вейвлет-коэффициенты получены с помощью дискретного вейвлет-преобразования. Результаты сведены в таблицу 3.

Таблица 3

Расчёт реактивной мощности, используя разные методики определения ивейвлет-преобразование

	Название способов определения мощности	Формула	Реактивная мощность
			, вар	, вар	, вар	, вар
1	Классическая		6005,7	1151,9	200,011	7357,6
2	Мощность по Буденау		6005,7	1151,9	200,011	7357,6
3	Мощность по Фризе		9999,4	1260,2	206,979	11843
4	Мощность по Шарону		6005,7	1151,9	200,011	7421,7
5	Мощность по Кастерсу-Муру		6005,7	1151,9	200,011	6429,7
6	Мощность по Зарнецкому		6002,6	1159,3	194,374	7421,7

Вывод

В данной работе ставилась цель не обосновать точность какой-либо методики определения реактивной мощности, а численно на конкретном примере сравнить существующие методы определения для нестационарных несинусоидальных сигналов. В расчётах использовались действующие значения токов и напряжений рассчитанных по классическим формулах, где интеграл заменён суммой и действующие значения токов и напряжений, полученные с помощью вейвлет-коэффициентов.

Литература:

1. Morsi, W. G. On the implementation of time-frequency transforms for defining power components in non-sinusoidal situations: A survey / W. G. Morsi// Electric Power Components and Systems. — 2009. — vol. 37. — №. 4. — P. 373–392.
2. Mazloomzadeh, A. Harmonic and Inter-harmonic Measurement Using Discrete Wavelet Packet Transform with Linear Optimization / 1.A. Mazloomzadeh, M. Mirsalim, H. Fathi // IEEE Conference on Industrial Electronics and Applications. — 2009. — P. 825–830.
3. Hamid, E. Y. Method for RMS and power measurements based on the wavelet packet transform / E. Y. Hamid, R. Mardiana and Z. I. Kawasaki// IEE Proceedings -Science, Measurement and Technology. — 2002. — vol. 149, No 2. — P. 60–66.
4. Barros, J. Application of the Wavelet-Packet Transform to the Estimation of Harmonic Groups in Current and Voltage Waveforms / J. Barros, R. I. Diego // IEEE Transactions on Power Delivery. — 2005. — vol. 21, No 1. — P. 533–535.
5. Morsi, W. G. Time-Frequency Non-sinusoidal Current Decomposition Based on the Wavelet Packet Transform / W. G. Morsi, M. E. El-Hawary. — IEEE Power Engineering Society General Meeting. — 2007. P. 1–8