В данной статье представлена связь между несобственными интегралами первого рода и несобственными интегралами второго рода, а также особые приемы вычисления несобственных интегралов. Если имеется значение некоторого, не берущегося элементарно, несобственного интеграла, то методом поворота координат и переходом к обратной функции можно отыскать значение еще нескольких не берущихся интегралов.
Перед изложением основных формул будет представлен несколько иной метод нахождения интеграла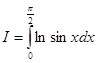 
Рассмотрим тождество:
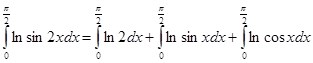(1)
которое очевидно справедливо, так как 
С другой стороны: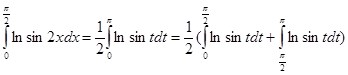 
В свою очередь,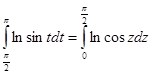 
(подстановка: 
)
Тогда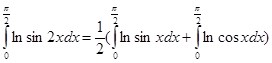 
,
и исходя из этого,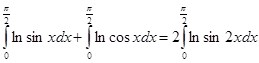 
Подставляя этот последний результат в формулу (1):
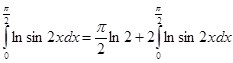
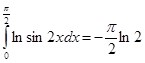(2)
Исходя из (2) и (1):
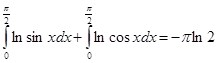(3)
Это тождество можно представить в виде: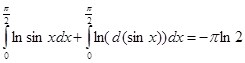 
, так как 
.
Если в интеграле 
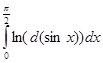произвести подстановку 
, то он будет иметь вид: 
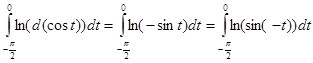. Последний интеграл подстановкой 
сводиться к интегралу: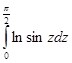 
Тогда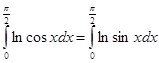 
, и на основании (3):
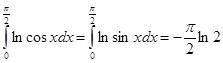(4)
Теорема 1:
1) Пусть 
непрерывна и строго возрастающая в 
, и 
. Тогда справедлива формула:
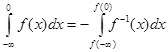(5)
2) Пусть непрерывна и строго спадающая в 
, и
. Тогда справедлива формула:
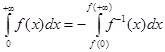(6)
Доказательство:
Ограничимся вторым случаем. Так как функция непрерывна и строго спадающая в , то она необходимо имеет и обратную функцию 
. Это дает возможность преобразовать несобственный интеграл первого рода в несобственный интеграл второго рода с особой точкой 
.
Сходимость или расходимость несобственных интегралов при подобных преобразованиях не нарушается.
Отыскание обратной функции к функции осуществляется по такому правилу: функцию следует преобразовать явно в виде 
, после чего поменять в ней переменные 
и 
местами, т.е. представить в виде 
. Последняя функция и будет обратной к функции , и обозначается: .
Пример 1: Пусть дана функция:
. Найти функцию обратную к ней.
, и меняя и местами: 
В дальнейших примерах (кроме примера 5-го и 6-го) будет показано, как имея значения лишь двух интегралов: 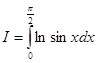и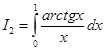 
, возможно определить специальными методами, в особенности поворотом координат, значения многих других интегралов, которые так же не берутся элементарно.
Пример 2: Вычислить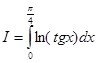 
, если известно, что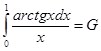 
Решение:
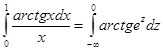(подстановка 
Применяя формулу (5):
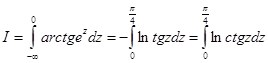
Тогда:
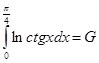(7)
Как известно, 
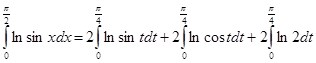(Подстановка 
)
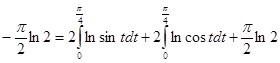
Исходя из последнего тождества и (7) выходит система из двух уравнений:
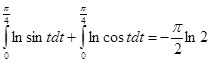
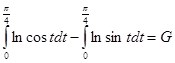
Прибавляя первое уравнение системы ко второму, находим:
,
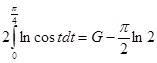и окончательно:
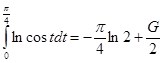(8)
Исходя из (7) и (8):
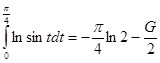(9)
И, исходя из (8) и (9), легко вывести окончательный результат:
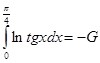(10)
В данном примере для отыскания решения интеграла (10) была применена в начале метода вычисления первая из формул теоремы 1, что сыграло немаловажную роль в отыскании значения данного интеграла.
Теорема 2:
Пусть непрерывна и строго спадающая (или строго возрастающая) в 
, 
– особая точка, 
, 
. Тогда справедлива формула:
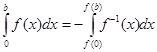(11)
Доказательство аналогичное доказательству теоремы 1. Только в этом случае несобственный интеграл второго рода преобразуеться в несобственный интеграл первого рода.
Пример 3: Вычислить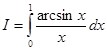 
в конечном виде.
С одной стороны 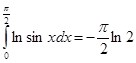; с другой стороны, по формуле (11):
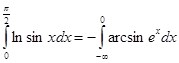
Применение формулы (11) оправдано, так как 
и особая точка:
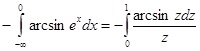(подстановка: 
).
Тогда: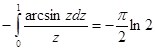 
И окончательный результат будет иметь вид:
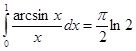
Теорема 3: Пусть непрерывна и строго спадающая (или строго возрастающая) в промежутке , 
, – особая точка. Тогда имеет место формула:
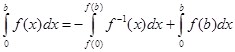(12)
Доказательство: начальные рассуждения аналогичны с теоремой 2, но в этом случае, в точке 
функция не достигает значения 
. Поэтому, если рассмотреть данный вопрос с геометрической точки зрения, т.е. усмотреть значение интеграла как площади, ограниченной некоторой осью с одной стороны и некоторой непрерывной интегрируемой функцией с другой, – то очевидно, уравнение (11) не будет полным, так как к значению интеграла от обратной функции необходимо прибавить площадь оставшегося прямоугольника с вершинами: 
, 
, 
, 
.
Пример 4: Вычислить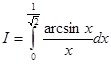 
Так как 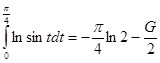, то принимая этот интеграл за начальную функцию, а искомый интеграл за обратную функцию, по формуле (12):
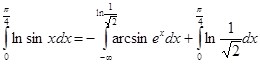
Подставляя в последнее тождество значение интеграла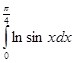 
и преобразуя:
,
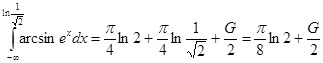далее подстановка: , которая приводит к окончательному результату:
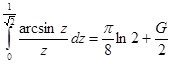(13)
Исходя из (13) можно получить разложение:
Обобщенные формулы:
, 
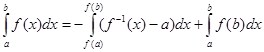
– особая точка (14)
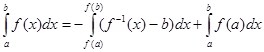
, – особая точка (15)
Обе формулы представляют собою преобразование несобственного интеграла второго рода в несобственный интеграл первого рода. Формула (14) выводиться из формулы (12) параллельным перемещением оси 
из начального положения в особую точку . При этом все условия существования несобственного интеграла первого рода, полученного из несобственного интеграла второго рода – сохраняются. Формула (15) являет собою аналог (14) в случае особой точки .
Пример 5: 
При преобразовании этого интеграла по формуле (14) – выходит аналогичный результат:
Пример 6: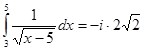 
Его вычисление по формуле (15) дает аналогичный результат:
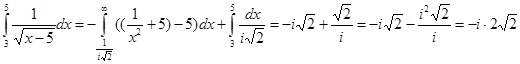
Пример 7: Вычислить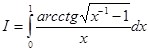 
Если обратиться вновь к тождеству 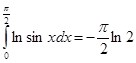и провести ряд элементарных преобразований, то выходит:
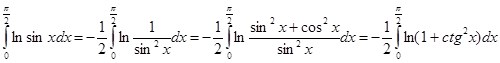
Отсюда следует: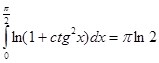 
Согласно формуле (11), так как условия теоремы 2 в этом случае соблюдены:
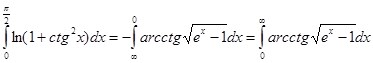
После подстановки: интеграл будет иметь вид:
Окончательная подстановка 
приводит к ответу:
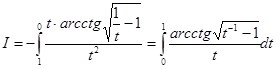
Таким образом, выходит результат:
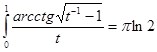(16)
Литература:
1. Прудников А.П., Брычков Ю.А., Маричев О.И. Интегралы и ряды, Изд-во: «Наука», 1981 г. – 797 с.
2. Бакельман И.Я. Высшая геометрия, Изд-во: «Просвещение», 1967 г. – 367 с.
