Теорема о спектральном разложении самосопряженных линейных операторов, по мнению многих авторов, является одной из самых удачных математических абстракций. Она имеет множество приложений в функциональном анализе и в математической физике и играет существенную роль в обосновании квантовой механики. С тех пор как эта теорема была впервые доказана Д. Гильбертом, ее содержание значительно расширилось. В настоящем сообщении построено спектральное разложение симметрического оператора, порожденного в гильбертовом пространстве, функций суммируемых с квадратом модуля, некоторой обобщенной квазидифференциальной операцией.
Рассмотрим симметрический оператор 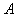 , действующий в гильбертовом пространстве
, действующий в гильбертовом пространстве 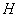 и имеющий плотную в пространстве
и имеющий плотную в пространстве 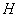 область определения
область определения 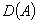 . Оператор
. Оператор 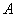 не предполагается самосопряженным, так что он является частью сопряженного с ним оператора
не предполагается самосопряженным, так что он является частью сопряженного с ним оператора 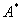 . В общем случае
. В общем случае 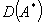
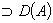 .
.
Функция 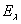 , определенная для любого вещественного
, определенная для любого вещественного 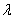 , называется спектральной функцией оператора
, называется спектральной функцией оператора 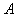 , если выполнены следующие условия:
, если выполнены следующие условия:
а) для любого вещественного 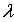
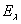 есть позитивный оператор;
есть позитивный оператор;
б) для любого элемента 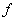 гильбертова пространства
гильбертова пространства 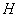 в котором рассматриваются
в котором рассматриваются 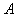 и
и 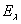 ,
, 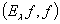
 не убывает при возрастании параметра
не убывает при возрастании параметра 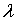 ;
;
в) для любого элемента 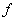 гильбертова пространства
гильбертова пространства 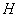
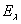 есть непрерывная слева в смысле нормы элемента функция параметра
есть непрерывная слева в смысле нормы элемента функция параметра 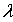 ;
;
г) для любого элемента 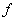 гильбертова пространства
гильбертова пространства 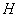
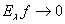 , если
, если
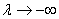 , и
, и 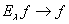 , если
, если 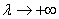 . Причем эти предельные соотношения рассматриваются в смысле нормы элемента;
. Причем эти предельные соотношения рассматриваются в смысле нормы элемента;
д) если 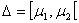 — любой конечный промежуток и
— любой конечный промежуток и 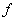 - любой элемент из пространства
- любой элемент из пространства 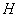 , то имеют место соотношения:
, то имеют место соотношения:
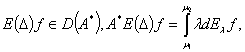 (1)
(1)
где 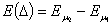 .
.
1. Спектральная функция называется ортогональной, если 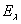 есть оператор ортогонального проектирования при любом вещественном значении
есть оператор ортогонального проектирования при любом вещественном значении 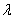 . Если оператор
. Если оператор 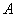 - самосопряженный, то он имеет только одну спектральную функцию и она — ортогональна. Обратно, всякая ортогональная спектральная функция однозначно определяет самосопряженный оператор
- самосопряженный, то он имеет только одну спектральную функцию и она — ортогональна. Обратно, всякая ортогональная спектральная функция однозначно определяет самосопряженный оператор 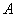 . Если же оператор
. Если же оператор 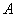 несамосопряженный, то он имеет неортогональные спектральные функции.
несамосопряженный, то он имеет неортогональные спектральные функции.
Согласно известной теореме М. А. Наймарка, для любой спектральной функции 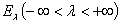 оператора
оператора 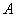 существует в некотором гильбертовом пространстве
существует в некотором гильбертовом пространстве 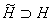 такое самосопряженное расширение
такое самосопряженное расширение 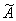 оператора
оператора 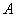 , что ортогональная спектральная функция
, что ортогональная спектральная функция 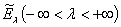 оператора
оператора 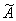 связана с
связана с 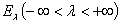 формулой
формулой
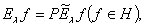 (2)
(2)
где 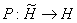 — оператор ортогонального проектирования.
— оператор ортогонального проектирования.
Учитывая (1), можно рассматривать равенство
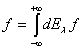 (3)
(3)
как разложение по обобщенным собственным элементам оператора 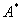 .
.
Для спектральных функций 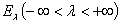 симметрического оператора
симметрического оператора 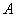 , действующих в абстрактном гильбертовом пространстве, показано, что и в этом случае имеются «краевые условия», зависящие от параметра
, действующих в абстрактном гильбертовом пространстве, показано, что и в этом случае имеются «краевые условия», зависящие от параметра 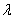 , которым удовлетворяют обобщенные собственные элементы оператора
, которым удовлетворяют обобщенные собственные элементы оператора 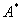 , участвующие в разложении (3).
, участвующие в разложении (3).
Пусть 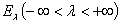 — какое-либо разложение единицы в
— какое-либо разложение единицы в 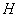 , а
, а 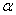 и
и 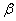 — фиксированные вещественные числа. Обозначим через
— фиксированные вещественные числа. Обозначим через 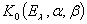 линейное многообразие векторных функций
линейное многообразие векторных функций 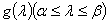 , принимающих значения в гильбертовом пространстве
, принимающих значения в гильбертовом пространстве  и допускающих представление
и допускающих представление 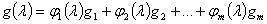 , где
, где 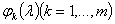 — произвольные непрерывные комплекснозначные функции параметра
— произвольные непрерывные комплекснозначные функции параметра 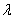 , а
, а 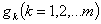 — произвольные элементы из пространства
— произвольные элементы из пространства 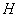 . Для различных векторных функций эти элементы и их число могут быть разными.
. Для различных векторных функций эти элементы и их число могут быть разными.
Для любых вектор-функций 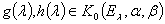 существует интеграл
существует интеграл
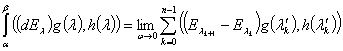 , (4)
, (4)
где 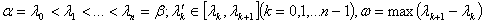 .
.
Введем в рассмотрение совокупность 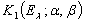 вектор-функций
вектор-функций 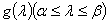 , которые принимают значения в пространстве
, которые принимают значения в пространстве 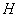 , и, кроме того, удовлетворяют следующему условию: при любом
, и, кроме того, удовлетворяют следующему условию: при любом 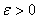 для функции
для функции 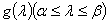 существует такая функция
существует такая функция 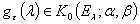 , что выполняется следующее условие:
, что выполняется следующее условие: 
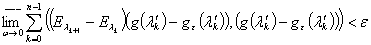 , где
, где 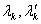 и
и 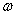 имеют прежний смысл. Множество
имеют прежний смысл. Множество 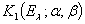 является, очевидно, линейным многообразием и вместе с векторной функцией
является, очевидно, линейным многообразием и вместе с векторной функцией 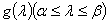 ему принадлежит также
ему принадлежит также 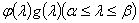 , какова бы ни была непрерывная комплекснозначная функция
, какова бы ни была непрерывная комплекснозначная функция 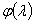 . Легко убедиться, что при любых
. Легко убедиться, что при любых 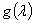 и
и 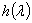 из совокупности
из совокупности 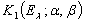 существует интеграл (4).
существует интеграл (4).
Если значения интеграла (4) принять за скалярное произведение 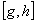 векторных функций
векторных функций 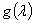 и
и 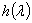 , то
, то 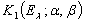 превратится в гильбертово пространство, в общем случае — неполное. Пополнение пространства
превратится в гильбертово пространство, в общем случае — неполное. Пополнение пространства 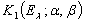 является, очевидно, пополнением и для пространства
является, очевидно, пополнением и для пространства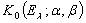 в этой же метрике. Заметим, что пополнение пространства
в этой же метрике. Заметим, что пополнение пространства 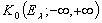 совпадает по существу с пространством
совпадает по существу с пространством 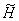 , которое можно использовать при оценке кратности спектра самосопряженного расширения оператора
, которое можно использовать при оценке кратности спектра самосопряженного расширения оператора 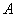 [1].
[1].
Лемма. Если 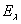 есть спектральная функция симметрического оператора
есть спектральная функция симметрического оператора 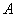 , то для любых вектор-функций
, то для любых вектор-функций 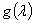 ,
, 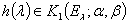 существует операторный интеграл Стилтьеса
существует операторный интеграл Стилтьеса 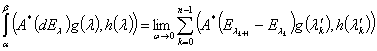 и имеет место формула
и имеет место формула 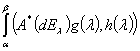 =
=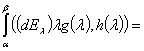
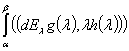 .
.
2. Пусть матрица 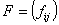 имеет размерность
имеет размерность 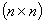 и составлена из комплекснозначных функций, определенных на интервале
и составлена из комплекснозначных функций, определенных на интервале 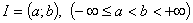 и удовлетворяющих следующим условиям:
и удовлетворяющих следующим условиям:
(i) 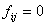 в интервале
в интервале 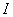 для индексов, удовлетворяющих неравенствам
для индексов, удовлетворяющих неравенствам 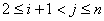 ;
;
(ii) 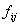 — локально суммируемы, т. е.
— локально суммируемы, т. е. 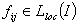 для
для 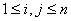 ;
;
(iii) 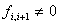 в
в  для
для  .
.
Определим квазипроизводные 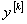 следующим образом:
следующим образом:
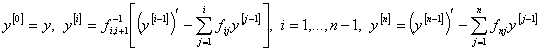 .
.
Этот подход к определению квазипроизводных и соответствующего формально самосопряженного квазидифференциального выражения предложен в работе [2]. В дальнейшем предполагаем, что функции 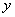 и их квазипроизводные до
и их квазипроизводные до 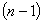 - го порядка включительно абсолютно непрерывны на любом компактном подынтервале промежутка
- го порядка включительно абсолютно непрерывны на любом компактном подынтервале промежутка 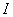 . Поскольку в дальнейшем будем рассматривать только симметрические квазидифференциальные выражения, то предположим, что матрица
. Поскольку в дальнейшем будем рассматривать только симметрические квазидифференциальные выражения, то предположим, что матрица 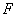 , кроме требований (i), (ii) и (iii), удовлетворяет также условию симметричности:
, кроме требований (i), (ii) и (iii), удовлетворяет также условию симметричности: 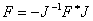 , где
, где 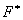 — матрица, сопряженная к матрице
— матрица, сопряженная к матрице 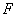 ,
, 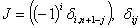 — символ Кронекера. Легко убедиться, что
— символ Кронекера. Легко убедиться, что 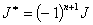 , где
, где 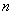 — натуральное число. Матрица
— натуральное число. Матрица 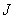 — косоэрмитова, если натуральное число
— косоэрмитова, если натуральное число 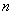 — четно, а матрицы
— четно, а матрицы 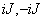 — косоэрмитовы, если натуральное число
— косоэрмитовы, если натуральное число 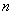 — нечетно. Можно считать, что скалярное дифференциальное выражение
— нечетно. Можно считать, что скалярное дифференциальное выражение 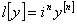 , где
, где 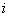 — мнимая единица, порождается матрицей
— мнимая единица, порождается матрицей 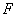 . Квазидифференциальная операция
. Квазидифференциальная операция 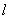 определяет минимальный замкнутый симметрический оператор
определяет минимальный замкнутый симметрический оператор 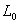 в гильбертовом пространстве
в гильбертовом пространстве 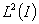 .
.
Пусть, например, 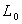 симметрический квазидифференциальный оператор с минимальной областью определения в пространстве
симметрический квазидифференциальный оператор с минимальной областью определения в пространстве 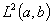 , порожденный квазидифференциальным выражением
, порожденный квазидифференциальным выражением 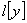 порядка
порядка 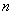 . Концы рассматриваемого промежутка
. Концы рассматриваемого промежутка 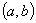 не предполагаются регулярными, т. е. могут быть сингулярными. В этом случае формула (3) реализуется в виде разложения по решениям уравнения
не предполагаются регулярными, т. е. могут быть сингулярными. В этом случае формула (3) реализуется в виде разложения по решениям уравнения
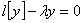 , (5)
, (5)
Решения уравнения (5) играют роль обобщенных собственных элементов оператора 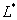 .
.
Для любых функций 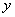 и
и 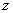 , к которым применима квазидифференциальная операция
, к которым применима квазидифференциальная операция 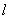 , имеет место обобщенная формула Лагранжа
, имеет место обобщенная формула Лагранжа
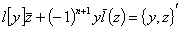 , (6)
, (6)
где 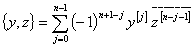 . Интегрируя почленно левую и правую части формулы Лагранжа (6), получим формулу Грина
. Интегрируя почленно левую и правую части формулы Лагранжа (6), получим формулу Грина
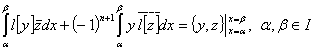 ,
,
где 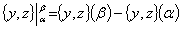 . Пусть
. Пусть 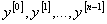 — квазипроизводные функции
— квазипроизводные функции 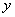 , а
, а 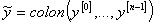 , составленный из этих квазипроизводных, — вектор-столбец. Заметим, что
, составленный из этих квазипроизводных, — вектор-столбец. Заметим, что 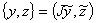 , где
, где 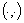 — скалярное произведение в
— скалярное произведение в 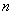 - мерном евклидовом пространстве. Матрица
- мерном евклидовом пространстве. Матрица 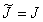 , если
, если 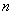 - четно, и
- четно, и 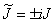 , если
, если 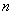 — нечетно, позволяет тождество Лагранжа можно переписать в виде
— нечетно, позволяет тождество Лагранжа можно переписать в виде 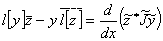 .
.
Теорема 1. Пусть 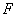 — матрица-функция, удовлетворяющая условиям: (i), (ii), (iii). Квазидифференциальная операция
— матрица-функция, удовлетворяющая условиям: (i), (ii), (iii). Квазидифференциальная операция 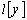 задана обычным образом. Дополнительно предположим, что функции
задана обычным образом. Дополнительно предположим, что функции 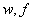 — локально суммируемы на рассматриваемом промежутке. Кроме того, предположим, что функция
— локально суммируемы на рассматриваемом промежутке. Кроме того, предположим, что функция 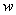 положительна на промежутке
положительна на промежутке 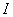 . Тогда для любого комплексного числа
. Тогда для любого комплексного числа 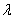 , любого вещественного числа
, любого вещественного числа 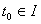 и любых комплексных чисел
и любых комплексных чисел 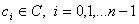 , существует единственное решение
, существует единственное решение 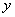 , заданное на промежутке
, заданное на промежутке 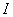 , начальной задачи
, начальной задачи 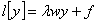 при условии
при условии 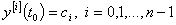 .
.
Доказательство в целом повторяет рассуждения, приведенные в [3, 4].
Теорема 2. Пусть 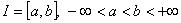 ,
, 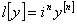 , матрица
, матрица 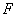 , удовлетворяет требованиям (i) — (iii) и условию симметричности. Тогда для любых комплексных чисел
, удовлетворяет требованиям (i) — (iii) и условию симметричности. Тогда для любых комплексных чисел 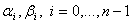 существует функция
существует функция 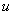 , принадлежащая области определения
, принадлежащая области определения 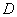 операции
операции 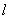 , такая что
, такая что 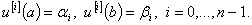
3. Как известно, каждой спектральной функции 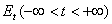 оператора
оператора 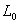
отвечает некоторая обобщенная резольвента 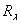 , определяемая формулой
, определяемая формулой
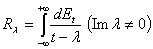 .
.
При помощи формулы обращения Стилтьеса спектральная функция 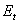 однозначно восстанавливается по обобщенной резольвенте
однозначно восстанавливается по обобщенной резольвенте 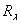 ; для любых функций
; для любых функций 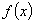 и
и 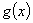 из
из 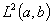 и любых вещественных
и любых вещественных 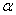 и
и 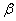 имеет место равенство:
имеет место равенство:
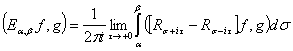 . (7)
. (7)
Равенство (7) позволяет построить формулу всех спектральных функций 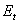 оператора
оператора 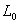 .
.
Пусть 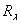 — какая-либо обобщенная резольвента оператора
— какая-либо обобщенная резольвента оператора 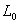 и
и 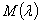 — ее характеристическая матрица. При любых вещественных
— ее характеристическая матрица. При любых вещественных 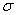 определим матрицу
определим матрицу 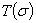 формулой
формулой
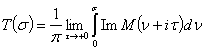 . (8)
. (8)
Формула (8) имеет смысл при любом вещественном 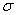 и
и 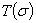 является неубывающей матричной функцией. Матрицу
является неубывающей матричной функцией. Матрицу 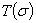 называют спектральной функцией распределения оператора
называют спектральной функцией распределения оператора 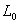 , соответствующей обобщенной резольвенте
, соответствующей обобщенной резольвенте 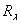 .
.
Пусть 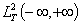 — гильбертово пространство
— гильбертово пространство 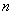 - мерных векторных функций
- мерных векторных функций 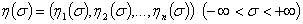 , которые будем рассматривать как одностолбцевые матричные функции; скалярное произведение в пространстве
, которые будем рассматривать как одностолбцевые матричные функции; скалярное произведение в пространстве 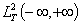 определяется формулой
определяется формулой 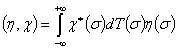 .
.
Теорема 3. Для любой функции 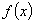
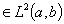 имеет место равенство
имеет место равенство 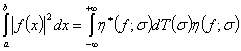 , где
, где 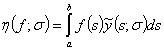 ; а несобственный интеграл
; а несобственный интеграл 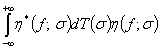 сходится в смысле метрики пространства
сходится в смысле метрики пространства 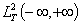 .
.
Литература:
1. Филиппенко В. И. Линейные квазидифференциальные операторы в гильбертовом пространстве // Исследования по функциональному анализу и его приложениям.- М.: Наука, 2006. С. 293–344.
2. Everitt, W. N. Generalized symmetric ordinary differential expressions 1: The general theory / W. N. Everitt, A. Zettl // Nieuw Archief Vood Wiskunde, 1979. — V. 27, № 3. — P. 363–397.
3. Филиппенко В. И. Обобщенные резольвенты неплотно заданного квазидифференциального симметрического оператора // Труды участников Международной школы-семинара по геометрии и анализу памяти Н. В. Ефимова, 5–11 сентября 2006 года. Ростов-на-Дону: Изд-во ООО «ЦВВР», 2006. — С. 167–169.
4. Фетисов В. Г. Исследования по теории операторов и их приложениям. Монография [Текст] / В. Г. Фетисов, В. И. Филиппенко. — Шахты: Изд-во ЮРГУЭС, 2008. — 185 с.







