В этой работе метод вариационных итераций использован к приближенному решению типичных линейных и нелинейных интегральные уравнения Волтерры. Результаты этого метода сходится быстрее к точному решению для некоторых нелинейных проблем. Метод вариационных итераций очень эффективные и простой.

Ключевые слова: интегральные уравнения, метод вариационных итераций, коррекция функционала, начальное приближение, последовательность функции, точное решение

Нелинейные явления, которые появляются во многих приложениях науки и техники, таком как гидро-аэродинамика, физика твердого тела, физика плазмы, математическая биология и химическая кинетика, может быть смоделирован обыкновенными уравнениями или уравнениями частными производных и интегральными уравнениями. Анализ научных работ, опубликованные ряд зарубежными учеными [1–5] показывают, что метод вариационных итераций (МВИ) и его модификации успешно применены ко многим приложениям прикладных наук. Новый метод был предложен ученым J. H. He в 1997 и систематический описан в 2000. До недавнего времени, приложение МВИ в нелинейных проблемах был разработан учеными и инженерами, потому что этот метод — самые эффективные и удобные и для слабо и для строго нелинейные уравнения. Метод является мощное устройство для решения различных видов уравнений, линейных или нелинейных. Интегральные уравнения Волтерры были решены классическим, числовым и теоретическим методы [4, 5]. Ниже МВИ применен для линейных и нелинейных интегральных уравнений Вольтерра.

Постановка задачи. Нелинейные уравнения в общем имеет вид

, (1)

где L, N — линейный и нелинейный оператор соответственно; g(t) — неоднородная часть уравнения; у — неизвестная функция.

Исходя из этого требуется решить следующую интегральную уравнению Вольтерра методом вариационных итераций [3]

, , (2)

где y(x) — искомая функция; f(x), F(y) — известные функции; K(x,t) — ядро интегрального уравнения (2).

Алгоритм метода вариационных итераций (МВИ). Для уравнения (1) методом вариационных итераций допускает коррекции функционала в виде [5]:

(3)

где — множитель Лагранжа.

Для приближенного решения уравнения (2) методом вариационных итераций сначала ее дифференцируем один раз по x, тогда

. (4)

Применяя идею МВИ к (3) имеем

. (5)

Вариации стационарного функционала

.

Для нахождения значения множителя Лагранжа составим уравнение Эйлера-Лагранжа , а для граничного значения . Отсюда .

Окончательная итерационная формула:

. (6)

Приложение. Ниже решены несколько примеры посвященные к решению проблемы (1) методом вариационных итераций.

Пример 1. Сначала рассмотрим самый простой пример. Требуется решить следующую линейную интегральную уравнению Вольтерра [5, 6]:

. (7)

Сначала дифференцируем уравнение (7) один раз по х: .

Используя формулу (6) запишем следующую итерационную формулу:

. (8)

Выбираем начальное приближение как . Дальнейшие приближения вычисляем по (8):

;

;

;..., .

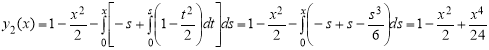Тогда . Это и есть точное решение уравнение (7).

Результаты ошибки аппроксимации (8) при n = 3 представлен на рис. 1.

Пример 2. Теперь рассмотрим чуть сложнее пример. Требуется решить следующую линейную интегральную уравнению Вольтерра [6]:

. (9)

Сначала дифференцируем уравнение (9) один раз по х:

.

Используя формулу (6) запишем следующую итерационную формулу:

. (10)

Выбираем начальное приближение как . Дальнейшие приближения вычисляем по формуле (10):

; ; ,....

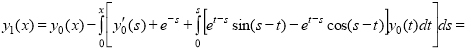
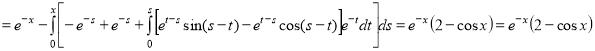
Точное решение уравнение (9): . Результаты ошибки аппроксимации (10) при n = 3 представлен на рис. 2.

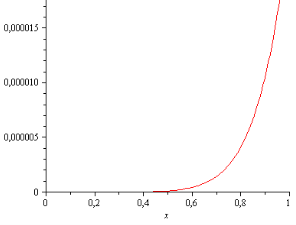
Рис. 1.

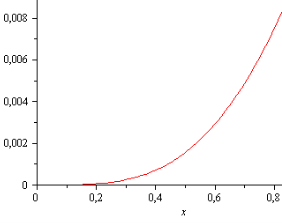
Рис. 2.

Пример 3. Теперь усложняем пример. Требуется решить следующую простую нелинейную интегральную уравнению Вольтерра [5]:

. (11)

Сначала дифференцируем уравнение (11) один раз по х:

.

Используя формулу (6) запишем следующую итерационную формулу:

. (12)

Выбираем начальное приближение как . Дальнейшие приближения вычисляем по формуле (12): ; ;....

Точное решение уравнение (11): .

Пример 4. Требуется решить следующую нелинейную интегральную уравнению Вольтерра [6]:

. (13)

Сначала дифференцируем уравнение (13) один раз по х:

.

Используя формулу (6) запишем следующую итерационную формулу:

. (14)

Выбираем начальное приближение из разложения в ряд Тейлора функции , т. е. . Дальнейшие приближения вычисляем по формуле (14) с помощью математического пакета Maple и получим следующие результаты: ; ;....

Тогда точное решение уравнение (13): .

Пример 5. Требуется решить следующую нелинейную интегральную уравнению Вольтерра [5]:

, . (15)

Сначала дифференцируем уравнение (15) один раз по х:

.

Используя формулу (6) запишем следующую итерационную формулу:

. (16)

Выбираем начальное приближение из разложения в ряд Тейлора функции , т. е. . Дальнейшие приближения вычисляем по формуле (16) с помощью математического пакета Maple и получим следующие результаты: ; ;....

Тогда точное решение уравнение (15): .

Пример 6. Требуется решить следующую нелинейную интегральную уравнению Вольтерра [4]:

, . (17)

Сначала дифференцируем уравнение (17) один раз по х: .

Используя формулу (6) запишем следующую итерационную формулу:

. (18)

Выбираем начальное приближение из разложения в ряд Тейлора функции , т. е. . Дальнейшие приближения вычисляем по формуле (18) с помощью математического пакета Maple и получим следующие результаты: ; ;....

Тогда точное решение уравнение (17): .

Выводы. Вэтой работе метод вариационных итераций успешно применен к решению интегральных уравнений Волтерры. Метод полезен и для линейных и для нелинейных уравнений. Этот метод очень силен и эффективен для нахождения точных и приближенных решений для широких классов проблемы. Этот метод не требует утомительных алгебраических вычислений. Для нелинейного уравнения это возникает часто, чтобы выразить нелинейное явление. МВИ облегчает вычислительную работу и дает решение быстро. Результаты показал, что метод очень точен и прост.

Литература:

1. He. J.H., A new approach to nonlinear partial differential equations, Commum. Nonlinear Sci. Numer. Simulation, 2(4), 1997, 230–235.
2. He. J.H., Variational iteration method a kind of non-linear analyticaltechnique: some examples, International Journal of Non-Linear Mechanics, 34(4), 1999, 699–708.
3. He. J.H., Variational iteration method-Some recent results and new interpretations, Journal of Computational and Applied Mathematics, 207, (2007), 3–17.
4. Wazwaz A. M. A First Cours in Integral Equations. Second Edition. Chicago: Saint Xavier University, 2015. — 331 p.
5. Wazwaz A. M. Linear and Nonlinear Integral Equations: Method and Applications. Chicago: Saint Xavier University, 2011. — 658 p.
6. Mamatov Sh.S., Abdirashidov A. Integral tenglamalarni taqribiy yechish usullari. Uslubiy qo‘llanma. — Samarqand: SamDU nashri, 2014. — 124 bet.