Численное моделирование и исследование переходных процессов при высокоскоростном ударе цилиндрического тела о жесткую преграду

Разработаны алгоритмы и комплекс программ для моделирования на ПК переходных процессов в твёрдом деформируемом теле. Решается задача об ударе цилиндрического тела о жесткую преграду с учётом выхода переднего фронта волны за зону контакта, когда на границе заданы предельные условия взаимодействия: 1) полное прилипание и 2) отсутствие трения.

Algorithms and complex of programs for modeling on the IT of transients process in rigid deformable body are developed. The task about impact of a cylindrical body to rigid barrier is solved in content of exit of a forward wave front out of a zone of contact when on boundary conditions of interaction are set: 1) a full adhesion and 2) lack of friction.

Интерес к задачам высокоскоростного соударения деформируемых тел продиктован необходимостью детального изучения протекающих при этом переходных процессов. Именно в эти промежутки времени происходят возрастания напряжений и температур до максимальных значений, переход материалов из одного состояния в другое, развивается зона контакта. Знание этих закономерностей служат при расчётах на прочность деталей машин, подвергающихся в процессе работы ударным нагрузкам и различного рода конструкций, внедряющихся с малыми и большими скоростями в деформируемую среду, при создании противометеоритной защиты космических аппаратов и. т.п.

Как известно, стремления к математическому моделированию переходных процессов при ударе в особенности проявляется в тех областях знания, где прямой эксперимент, позволяющий собрать достаточно полную и объективную информацию об исследуемой реальности, практически невозможен. Кроме того, в случаях когда уравнения состояния среди часто самоопределяется путём изучения распространения пластических волн, возникают трудности правильной интерпретации экспериментальных данных, полученных в условиях высоких скоростей нагружения, когда необходимо учитывать процесс распространения волн. Объяснения этих явлений способствуют развитию теории распространения упругопластических волн и распространения ударных волн, допущениях и позволяющем в то же время ставить разрешаемые математические задачи.

При классическом подходе исследование сплощных сред, начинают обычно с изучения свойств бесконечно малых элементов рассматрываемой области, устанавливают соотношения между средними значениями различных величин, связанных с рассматриваемыми бесконечно малыми элементами, а затем, устремляя размеры элементов к нулю при неограниченном возрастании их числа, получают дифференциальные уравнения в частных производных описывающие поведение области.

В противоположность классическому подходу в настоящее время широко используется подход, основанной на представлении сплощной среды в виде множества конечного числа элементов, соединенных между собой в конечном числе узлов на границе между ними [1]. При такой пространственной дискретизации геометрия объекта с достаточной полнотой сохраняется в идеализированной модели.

При установлении свойств отдельных элементов могут использоваться уравнение, описывающие поведения области, но размеры элементов все время остаются конечными, дифференциальные уравнения в частных производных заменяются системами алгебраических и обыкновенных дифференциальных уравнений.

При этом, если удовлетворяются некоторые условия полноты, то с увеличением числа элементов и уменьшением их размеров поведения дискретной системы приближается к поведению «непрерывной системы», т. е. сплошной среды.

Рассматривается плоская динамическая контактная задача о нормальном ударе цилиндрического полукольца о недеформируемому полуплоскость. Исследуется распространение волн в твердом теле при различных значениях скорости V₀ с предельными условиями взаимодействия в упругом материале:

1)     полное прилипание и 2) отсутствие трения.

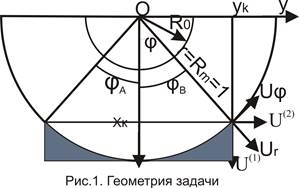
Пусть тело, имеющее в сечении форму полукольца с внутренним R₀ и внешним R_м радиусами движется с постоянной скоростью V₀ и в момент времени t=0 встречает абсолютно жесткую неподвижную преграду. В декартовой системе координат (х,у), связанной с телом, направление вектора скорости совпадает с осью Х, которая нормальна к поверхности преграды.

При решении задачи удобно обратить движение и считать, что деформируемое тело до удара находиться в состоянии покоя, а жесткая преграда налетает на него со скоростью — V_0. Для упругой среды из геометрии задачи (рис.1) определяется границы критической области, где скорость расширения зоны контакта будет превосходить скорость продольной вольны.

Требуется определить параметры движения в предположении, что первоначальное касание произошло в момент времени t=0 в точке и при различных допущениях относительно характера взаимодействия тел в процессе соударения.

Уравнение движения дискретной модели выводится в декартовой системе координат на основе вариационного принципа Гамильтона-Остроградского. Для более точной аппроксимации области тела конечно-элементная(КЭ) модель строится в цилиндрической системе координат с помощью регулярной сетки образованной

, ,

координатными линиями: r= R₀+i•?r, φ_j =j•?φ, а в некоторых случаях для удобства удовлетворения граничных условий переход из цилиндрической системы координат в декартовую осуществляется по формулам: x= R•cosφ, y=R•sinφ.

Уравнение движения для i-го узла сетки имеет вид:

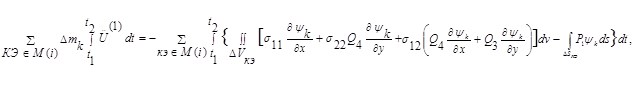
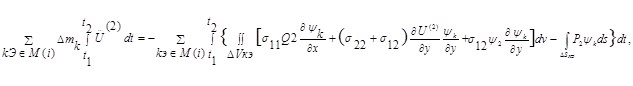где введены обозначения: , , , ;

U⁽¹⁾, U⁽²⁾-проекции вектора перемещений материальных частиц на оси декартовой системы координат; ψ_k(x,y)-функции формы используемого конечного элемента [1]. k-соответст-вующие локальные номера узла — i в кратных элементах данного узла; σ_pq-компоненты тензора напряжений (pq=11, 22, 12); p₁, p₂-нормальные и касательные к преграде составляющие поверхностных сил.

Границы тела вне зоны контакта считаются свободными от усилий. Вне зоны контакта удовлетворяются условия полного прилипания и отсутствия трения. В терминах скоростей и внешних сил эти условия соответственно записываются так:

V_nⁱ=-V₀•cosα, V_tⁱ=0; V_nⁱ=-V₀•cosα, P_εⁱ=0,

где i-принимает все значения из множества граничных узлов зоны контакта.

В качестве начальных условий берутся нулевые.

Шаг интегрирования ?t_рас⁽ⁿ⁾ определяется с учётом ограничений. С одной стороны этот шаг должен удовлетворят условию:  где 0≤  =const≤1,

?L-минимальный линейный размер элемента, a_max-максимальная скорость распространения возмущения, с другой стороны необходимо определить такой шаг ?t_рас⁽ⁿ⁾≤ ?t_кр⁽ⁿ⁾, который обеспечил бы достаточно точное попадания граничных узлов в зону контакта. Предусмотрен вариант перерасчёта в случае перелёта узла за преграду.

Расчёты для линейной среды проведены в цилиндрической системе координат в расчётной области R₀=0,5; R_m=1; φ₀=0; φ_n=0,4; ?r=0,01; ?φ=0,01 со скоростями удара V₀=-0,05 и V₀=-0,1, когда параметры, характеризующие экспериментальные функции взяты в виде [2]:

σ=(λ+2/3•µ)•ε; σ_i=3•µ•ε_i;где λ=0,43; µ=0,285; ε-объёмная деформация, ε_i-интенсивность деформации.

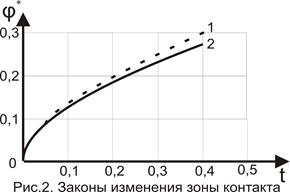
На рис.2 для сопоставления кривых, описывающих зависимости крайней точки зоны контакта от времени в случаях полного прилипания (линия-2) и отсутствия трения (линия-1), приводятся результаты, полученные с идентичными параметрами расчёта. Расчёты показали, что эти кривые в сверхзвуковом режиме расширения крайней точки зоны контакта (t`=0,05) полностью совпадают и начиная с t≥t`в случае отсутствия трения кривая проходит чуть выше, чем во втором случае.

На рис.3 приведены эпюры касательной к преграде, составляющей вектора скорости для различных моментов времени. Звёздочкой на оси абсцисс помечены положения крайней точки зоны контакта для соответствующих моментов времени.

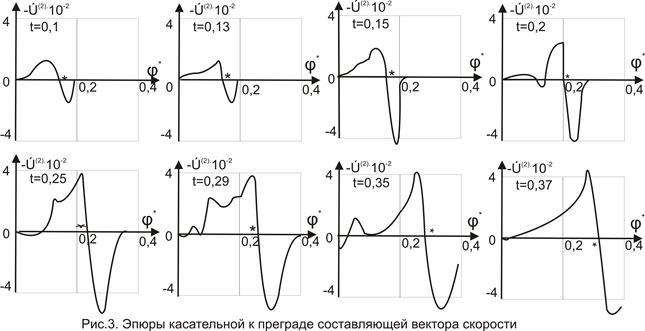
В зоне контакта при гладкой преграде нет монотонного изменения тангенциальной составляющей скорости частиц. Расчёты показывают, что Ú⁽²⁾ с течением времени и расширением зоны контакта меняет знак. Если в начальный момент времени (0≤t≤0,15) между осью симметрии и φ^*, Ú⁽²⁾<0 и увеличивается при приближении к φ^*, то при t ≥0,2 в зоне контакта есть точки где Ú⁽²⁾>0. Справа и слева от крайней точки зоны контакта тангенциальная скорость имеет разные знаки. Причём знаки таковы, что точки тела движутся в противоположные стороны от точки контакта. В самой точке разрыв.

Дополнительные возмущения, порожденные крайней точкой зоны контакта, распространяются вдоль границы контакта и со временем достигают оси симметрии φ=0.

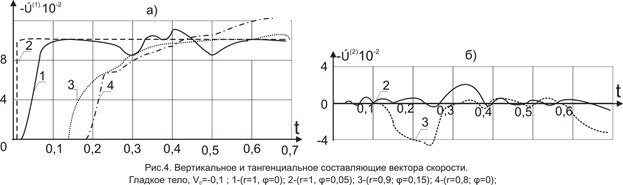
При этом в интервале времени (0,2; 0,25) скорости Ú⁽²⁾ вточках вблизи оси φ=0 меняют знак. В частности, в точке (r=0; φ=0,05) положительные значения появляются, начиная с момента времени t ≥0,22. Это видно из рис.4(б) где показано изменение во времени тангенциальной составляющей вектора скорости в точках ((r=1; φ=0,05) –сплошная линия) и ((r=0,9; φ=0,15) –пунктирная линия) на границе и во внутренней точках тело соответственно.

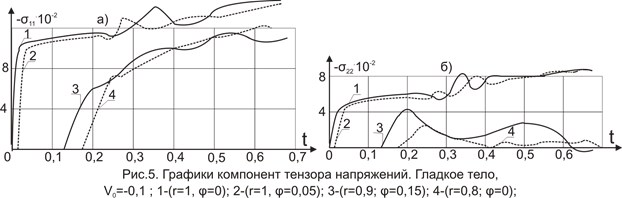
На рис.5 приведены графики изменения во времени компонент тензора напряжений σ₁₁ и σ₂₂ вхарактерных точках (r=1; φ=0), (r=0,8; φ=0) на оси симметрии, в сечении r=1, (r=1; φ=0,05) внутри тела (r=0,9; φ=0,15). Здесь в отличии от случая полного прилипания, в точках на внешней поверхности тела имеет место колебания указанных величин. При этом момент его появления совпадает со временем начала изменения знака кривой Ú⁽²⁾ в данных точках.

Изменение во времени вертикальной составляющей вектора скорости Ú⁽¹⁾ в фиксированных точках (r=0,05; φ=0); (r=0,8; φ=0); (r=1; φ=0,05); (r=0,9; φ=0,05) кривая Ú⁽¹⁾ подвергается изменению в сверхзвуковом режиме расширения зоны контакта с момента времени подходе данной точки к преграде и скачком возрастает, определяя величину скорости удара V₀=-0,1 и в дальнейшем остается постоянной. Вертикальное движение в точке (r=0,95; φ=0) на оси симметрии появляется на фронте продольной вольны, на котором скорость Ú⁽¹⁾ скачком возрастает до значения в точке (r=1; φ=0,05). На фронте поперечной волны кривая изменяется непрерывно. Это продолжается до момента времени (t≈0,25) прихода в данную точку возмущений, распространяющихся вдоль границы контакта. Влияние последнего, как подтвердили расчёты, с глубиной уменьшается.

Таким образом поставленная цель разработки алгоритмов и комплекс программ, представляющие интегрированную среду, как инструмент организации и проведения вычислительных экспериментов по исследованию переходного процесса при ударе цилиндрического кольца о жесткую преграду достигнута.

Литература:

1.                       Зенкевич О., Чанч И. Метод конечных элементов в теории сооружений и в механике сплошных сред. -М.: Недра, 1974. -240 с

2.                       Рахматуллин Х. А. Сагомонян А. Я., Алексеев Н. А. Вопросы динамики грунтов. –М.: Недра, 1967. — 232 с

3.                       Бадалов Ф. А. Метод степенных рядов в линейной теории вязко упругости. — Ташкент.: Фан, 1980. -221 с.