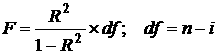Планирование финансовых потоков торговой фирмы с помощью модели прогнозирования продаж

На современном этапе развития формируется рыночно ориентированная система национального хозяйства, сфера торговли в России во многом приблизилась к международным требованиям, она входит в десятку крупнейших в мире и в пятерку наиболее крупных европейских рынков. Развитие отрасли торговли носит важный характер для экономики страны, связанный с повышением жизненного уровня людей, созданием ВВП, формированием доходной базы бюджета РФ, внедрением инноваций и достижением научно-технического прогресса, обеспечением национальной товарной безопасности, наращиванием конкурентных преимуществ российских предприятий. В связи с этим приобретает важное значение выработка новых способов и подходов к технологиям управления от руководителей торговых организаций, в том числе в области финансового менеджмента. В настоящее время первоочередной задачей руководства торгового предприятия становится обеспечение фирмы финансовыми ресурсами в размере, удовлетворяющем ее обязательства. В статье предлагается модель прогнозирования продаж с целью планирования финансовых потоков торговой фирмы.

Для построения прогноза будет проанализирован временной ряд продаж торгового предприятия за 2010–2011гг. На предприятии нет четкой информации о продаже по месяцам, данная информация присутствует в разрезе кварталов, поэтому разработаем модель для поквартального разбития, однако в последствие будет возможность осуществлять прогноз по месяцам. Данные о продажах предприятия представлены в Таблице 1.

Таблица 1

Объем продаж за 2010–2011 гг.

Источник: Составлено автором

При наличии во временном ряду тенденции и циклических колебаний значения каждого последующего уровня ряда зависят от предыдущих. Корреляционную зависимость между последовательными уровнями временного ряда называют автокорреляцией уровней ряда.

Количественно её можно измерить с помощью линейного коэффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени.

Рассмотрим автокорреляцию данного временного ряда (рис.1), данные по автокорреляции представлены в таблице 2.

Таблица 2

Автокорреляция функции объемов продаж за 2008–2009 г.

Источник: Составлено автором

Анализ автокорреляционной функции и коррелограммы позволяет определить лаг, при котором автокорреляция наиболее высокая, а, следовательно, и лаг, при котором связь между текущим и предыдущими уровнями ряда наиболее тесная. То есть при помощи анализа автокорреляционной функции и коррелограммы можно выявить структуру ряда.

Если наиболее высоким оказался коэффициент автокорреляции первого порядка, исследуемый ряд содержит только тенденцию. Если наиболее высоким оказался коэффициент автокорреляции порядка ф, ряд содержит циклические колебания с периодичностью в ф моментов времени.

Анализ частичной автокорреляции указывает на значимую автокорреляцию на первом лаге и отсутствие таковой на всех последующих. Такая ситуация характерна для линейного тренда.

Прогнозная модель имеет вид y=а₀+ax₁+ax₂+ax₃+ax₄….+ax_n,

y = 270,5368–9,0843 x

где х- порядковый номер периода.

На следующем этапе проведем оценку мультиколлинеарности факторов, в качестве которых выступают обобщенные в таблице 3 показатели, влияющие на объемы продаж.

Таблица 3

Показатели, влияющие на объем реализации 2010–2011 гг.

Источник: Составлено автором

Проведенный корреляционный анализ показал, что присутствует высокая взаимозависимость между такими показателями (см. табл. 4).

На следующем этапе проведем оценку мультиколлинеарности факторов. Так, средствами корреляционного анализа было установлено, что зависимость между указанными временными рядами свидетельствует об отсутствии мультиколлинеарности, что делает возможным использование этих переменных в дальнейшем анализе.

Таблица 4

Корреляционная матрица показателей

Источник: Составлено автором

Поскольку исследуемые факторы определяют линейную функцию, то формируемая модель должна носить аддитивный характер. Таким образом, можно сформировать следующую модель, представленную в общем виде:

где V — объем продаж, тыс.р,

Q — Индекс роста покупательской способности контрагентов, %,

F — Курс доллара, руб. за 1 доллар.

S — Инфляция за период, %

Р — ставка по кредитам, %

Используя модуль «Множественная регрессия» пакета программ Statistica, была получена описанная выше модель. Оценку модели произведем по величине коэффициента детерминации (R2):

R² = 88,36 %

Очевидно, что полученная модель характеризуется высоким значением коэффициента детерминации, следовательно, необходимо оценить ее качество посредством расчета F-критерия и сравнения его величины с табличными значениями.

F-критерий Фишера вычисляется по формуле:

, (1)

где R² — коэффициент детерминации

df — количество степеней свободы:

n — количество наблюдений;

i — количество оцениваемых параметров;

Тогда, . Представленное значение превышает табличное для заданного количества степеней свободы. Таким образом, необходимо рассмотреть коэффициенты регрессии и уровень их статистической значимости.

По результатам оценки модели были получены данные, представленные в таблице 5.

Таблица 5

Значения и оценки регрессионных коэффициентов

Источник: Составлено автором

Таким образом, полученные коэффициенты математической модели являются статистически значимыми, а сама модель имеет вид:

Можно сформировать следующие модели, представленные в общем виде:

М1:

М2:

М3:

М4:

М5:

Оценку моделей произведем по величине коэффициента детерминации (R2):

R²_М1 = 95,53 %

R²_М2 = 99,42 %

R²_М3 = 95,20 %

R²_М4 = 95,51 %

R²_М5 = 99,99 %

Очевидно, что полученные модели характеризуются высокими значениями коэффициента детерминации, следовательно, необходимо оценить их качество посредством расчета F-критерия и сравнения его величины с табличными значениями.

F-критерий Фишера вычисляется по формуле:

,

где R² — коэффициент детерминации

df — количество степеней свободы:

n — количество наблюдений;

i — количество оцениваемых параметров;

Тогда,

85,42

690,93

79,42

85,03

35053,85

Все представленные значения превышают табличное для заданных степеней свободы. Таким образом, необходимо рассмотреть коэффициенты регрессии и уровень их статистической значимости.

По результатам оценки модели М1 были получены данные, представленные в таблице 6.

Итак, модели М1, М2,М3,М5 характеризуются неудовлетворительными значениями показателя уровня статистической значимости (p-level). Следовательно, они непригодны для дальнейшего использования, а зависимость, подобранная на предыдущем этапе, носит случайный характер.

По результатам оценки модели М4 были получены данные, представленные в таблице 6.

Таблица 6

Значения и оценки регрессионных коэффициентов для модели М4

Источник: Составлено автором

В этой модели все качественные характеристики регрессионных коэффициентов удовлетворяют предъявляемым к ним требованиям. В качестве промежуточного итога можно рассматривать модель М4 как единственную, отвечающую всем требованиям по достоверности зависимости и характеру связи между показателями. Модель М4 является единственной статистически значимой моделью. Поэтому данная модель в дальнейшем будет рассматриваться как основная рабочая модель. Представляется целесообразным записать ее в окончательном варианте:

Смоделированные с помощью представленной модели данные позволяют оценить характер распределения остатков, равно как и саму величину расчетных значений (см. таблицу 7).

Таблица 7

Фактические и расчетные значения объемов продаж

Источник: Составлено автором

Таким образом, среднее отклонение расчетных значений объемов продаж от фактических составило 16,66 тыс.р.

В таблице 8 представлены сведения, отражающие численные значения объемов продаж в фактическом и смоделированном представлении, а также величину относительного отклонения этих показателей в каждый конкретный год.

Таблица 8

Сопоставление фактического и расчетного объемов продаж в 2010–2011

Источник: Составлено автором

Рассмотрим построение прогноза по данной модели на примере 2012 г. При прогнозе будут использоваться следующие условные сценарии:

1. Линейное изменение величины объемов на основе сложившейся тенденции (инерционный сценарий).

2. Изменение величины объемов продаж в соответствии с полученной моделью на основе инерционного приближения данных по анализируемым факторам (модельный сценарий).

3. Изменение величины объемов продаж в соответствии с полученной моделью на основе пессимистических прогнозов факторов (пессимистический модельный сценарий).

4. Изменение величины объемов продаж в соответствии с полученной моделью на основе оптимистических прогнозов факторов (оптимистический модельный сценарий).

Для построения прогноза по инерционному сценарию необходимо выделить уравнение линейного тренда, который описывает исходные данные в зависимости от фактора времени.

Для построения прогнозов по сценариям необходимо спрогнозировать факторы, заложенные в модель.

Применение двух подходов к прогнозированию (экстраполяция и метод декомпозиции) приводит к различным прогнозным результатам, что дает основания для усреднения полученных значений с целью получения окончательного инерционного прогноза.

Полученные данные позволяют рассмотреть экстраполяционный сценарий, в рамках которого линейный прогноз, полученный ранее, следует рассматривать как оптимистический вариант развития событий. Усредненный прогноз тогда следует рассматривать как инерционный, а прогноз, полученный с использованием декомпозиции временного ряда, — пессимистический.

Таким образом, были получены следующие прогнозные значения для показателя «Индекс роста покупательской способности контрагентов, %» (см. таблицу 9).

Таблица 9

Прогнозные значения показателя «Индекс роста покупательской способности контрагентов, %» на 2012 г.

Источник: Составлено автором

С использованием инерционного сценария может быть получен прогноз на восемь следующих периодов (поквартально 2010г.) показателя «Курс доллара, руб. за 1 доллар», уравнение тренда:

у=22.63+1.19х

где х — порядковый номер периода

Применение двух подходов к прогнозированию (экстраполяция и метод декомпозиции) приводит к различным прогнозным результатам, что дает основания для усреднения полученных значений с целью получения окончательного инерционного прогноза.

Полученные данные позволяют рассмотреть экстраполяционный сценарий, в рамках которого линейный прогноз, полученный ранее, следует рассматривать как пессимистический вариант развития событий. Усредненный прогноз тогда следует рассматривать как инерционный, а прогноз, полученный с использованием декомпозиции временного ряда, — оптимистический.

Таким образом, были получены следующие прогнозные значения для показателя «Курс доллара, руб. за 1 доллар» (см. таблицу 10).

Таблица 10

Прогнозные значения показателя «Курс доллара, руб. за 1 доллар» на 2012 г.

Источник: Составлено автором

Применение двух подходов к прогнозированию (экстраполяция и метод декомпозиции) приводит к различным прогнозным результатам, что дает основания для усреднения полученных значений с целью получения окончательного инерционного прогноза.

Полученные данные позволяют рассмотреть экстраполяционный сценарий, в рамках которого линейный прогноз, полученный ранее, следует рассматривать как пессимистический вариант развития событий. Усредненный прогноз тогда следует рассматривать как инерционный, а прогноз, полученный с использованием декомпозиции временного ряда, — оптимистический.

Таким образом, были получены следующие прогнозные значения для показателя «Инфляция за период, %» (см. таблицу 11).

Таблица 11

Прогнозные значения показателя «Инфляция за период, %» на 2010 г.

Источник: Составлено автором

Следовательно, применение двух подходов к экстраполяционному прогнозированию приводит к различным прогнозным результатам, что дает основания для усреднения полученных значений с целью получения окончательного инерционного прогноза.

Полученные данные позволяют рассмотреть экстраполяционный сценарий, в рамках которого линейный прогноз, полученный ранее, следует рассматривать как пессимистический вариант развития событий. Усредненный прогноз тогда следует рассматривать как инерционный, а прогноз, полученный с использованием декомпозиции временного ряда, — оптимистический.

Таким образом, были получены следующие прогнозные значения для показателя «ставка по кредиту, %» (см. таблицу 12).

Таблица 12

Прогнозные значения показателя «ставка по кредиту, %» на 2012 г.

Источник: Составлено автором

Таким образом, можно обобщить имеющиеся сведения о прогнозируемом развитии факторов в таблице 13 с целью построения прогнозных моделей.

Таблица 13

Прогнозы факторов в соответствии со сформированными сценариями

Источник: Составлено автором

Таким образом, полученные прогнозные значения факторов необходимо подставить в полученную модель объемов продаж с тем, чтобы рассчитать прогнозы на среднесрочную перспективу по трем сценариям. Расчет представлен в таблице 14.

Таблица 14

Расчет прогноза в соответствии с регрессионной моделью

Источник: Составлено автором

При дальнейшем анализе пессимистический вариант развития не будет рассматриваться, так как значения объемов продаж принимает отрицательные значения. К тому же, отрицательные значения нарастают с каждым кварталом и, в соответствии с пессимистическим прогнозом, отрицательные значения за 3 и 4 кварталы по отдельности значительно превышают объемы продаж за весь 2011 г, следовательно, вероятность данного варианта развития ничтожно мала.

Третий сценарий рассматривает наиболее оптимистичный вариант, но мало вероятный, так как значения за 3 и 4 кварталы по отдельности значительно превышают объемы продаж за весь 2011 г, следовательно, вероятность данного варианта развития тоже ничтожно мала. Сценарии 2 наиболее усредненную тенденцию возможности дальнейшего роста объемов продаж на рынке. В соответствии с инерционным сценарием, который кажется наиболее вероятным, уровень объемов продаж в 2012 будет составлять около 29857,35 тыс.р.

Для верификации прогноза сравним полученные прогнозные данные и и имеющиеся на предприятии данные о продажах за 3 квартала 2012 г., объем продаж составил 22593 тыс.р., а по расчетам прогноза эта сумма составляла 22589 тыс.р..

Таким образом, полученный прогноз характеризуется высокой степенью точности и может использоваться на предприятии.

Литература:

1. Анискин ЮЛ., Павлова А. М. Планирование и контроллинг. — М.: ОМЕГА-Л. 2011.

2. Тегюва Т. В. Эффективный финансовый директор. — М.: ЮРАЙТ, 2010.

3. Тимофеева ТВ. Анализ денежных потоков предприятия: Учеб. пособие. — 3-е изд. — М.: Финансы и статистика: ИНФРА-М. 2010.

4. Экономико-математические методы и прикладные модели: Учебное пособие для вузов/ Под ред. В. В. Федосеева. — М.: ЮНИТИ, 2001.