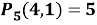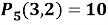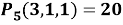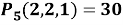В статье рассмотрены варианты решения ключевых задач, которые можно воспроизвести во многих других задачах, различных по содержанию, и тем самым получить ключ к их решению.
Ключевые слова: комбинаторика, ключевые задачи.
Рассмотрим 10 вариантов задач, какие позволительно назвать ключевыми : вних встречаются ситуации, которые можно воспроизвести во многих других задачах, различных по содержанию, и тем самым получить, ключ к их решению.
1. Сколькими способами можно 5 различных предметов пронумеровать цифрами 1, 2 и 3?
Чтобы выполнить условие задачи, нужно из цифр 1, 2, 3 составить пятициферную комбинацию. Например, одной из них будет:
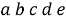
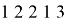
Если мы изменим порядок цифр в этой комбинации, то так как предметы различны, получим новый вариант нумерации. Следовательно, порядок элементов имеет значение, тогда мы имеем дело с размещениями из трех элементов по пять, разумеется, с повторениями.
Ответ:
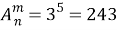
2. Сколькими способами можно 5 одинаковых предметов пронумеровать цифрами 1, 2 и 3?
Также из трех цифр надо составить пятициферные комбинации, например:
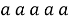
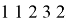
Но в отличие от предыдущей задачи здесь существенно только то, сколько каких цифр использовано, а в каком порядке они взяты роли не играет. Все предметы одинаковы, и будут ли две единицы стоять под первым и вторым предметами или, скажем, под третьим и пятым — безразлично. Важно лишь, что единиц использовано две. Получающиеся пятициферные комбинации будут только тогда различны, когда они будут отличаться хотя бы одной использованной цифрой. Значит, в данной задаче мы имеем дело с сочетаниями, с повторениями:
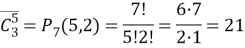
3. Сколькими способами можно
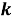
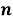
Задачу можно интерпретировать так: каждому предмету нужно указать номер ящика. Иными словами, требуется из
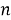
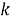
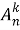
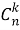
4. Множество состоит из
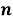
Всякое выделение подмножества из данного множества состоит в том, что для каждого элемента мы определяем, принадлежит он данному подмножеству или не принадлежит. Иными словами, каждому элементу сопоставляем один из двух символов:
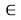
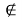
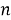
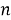
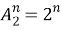
Но можно предложить и совсем иной путь подсчета числа подмножеств, а именно составить полную систему событий. Подмножество может быть пустым, может иметь 1, 2, …, n элементов. В каком порядке включаются элементы в подмножество, значение не имеет; важно лишь, какие именно. Поэтому число двухэлементных подмножеств равно числу сочетаний без повторяющихся элементов из
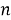
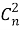
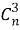
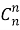
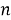
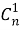
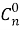
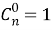
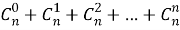
Сопоставляя этот ответ с тем же числом подмножеств, найденным другим путем, приходим к равенству
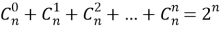
5. Сколькими способами из колоды в 36 карт можно выбрать 4 карты так, чтобы среди них: а). не было ни одного туза; б). был хотя бы один туз; в). был один туз; г). было не более двух тузов и один валет?
Отметим, что два набора карт будут различными, если они отличаются хотя бы одной картой. Порядок же карт значения не имеет, т. е. в данной задаче комбинации являются сочетаниями. В колоде нет одинаковых карт, значит, сочетания будут без повторяющихся элементов.
а). В колоде 4 туза и 32 карты, не являющимися тузами. Из последних и образуются наборы карт, не содержащие тузов. Значит, их число равняется:
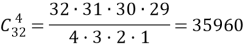
б). Всевозможных наборов карт имеется
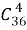
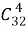
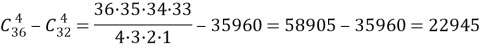
в). Один туз из четырех можно выбрать
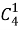
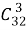
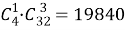
г). Не более двух тузов — это один туз, или один туз, или два туза. Кроме того, должен быть один валет (из четырех) и остальные какие угодно карты, но не являющимися тузами и валетами; будем называть их «другие карты».
Значит, полная система событий для данной задачи такова: или три другие карты и один валет; или две другие карты, один валет и один туз; или одна другая карта, один валет и два туза.
В каждой строке логическая связка «и»; между строками — логическая связка «или». Всех других карт, не являющихся тузами и валетами, 28. Выбрать три из них можно
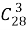
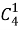
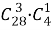
Один туз можно выбрать
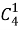
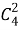
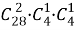
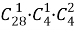
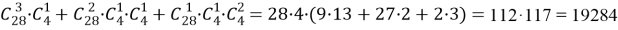
6. Через узкий длинный проход укротитель должен выпустить на арену 5 львов и 4 тигра. Звери будут идти один за одним, но при этом никакие два тигра не должны оказаться рядом. Сколько имеется способов такой расстановки зверей?
Согласно условию, каждый тигр должен находиться между львами либо идти первым или последним. Это значит, что расстановку зверей можно изобразить так: — Л — Л — Л — Л — Л –, где буквы Л обозначают львов, а черточки «–» места, где могут находиться тигры. Из этих 6 мест нужно выбрать любые 4. Так как звери индивидуальны, то порядок, в котором они занимают места, также следует принимать во внимание.
Значит, число возможных расстановок тигров равняется
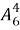
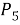
Ответ:
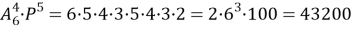
В задаче б требовалось найти число комбинаций при условии сохранения определенного расположения элементов. Их можно назвать «комбинации с ограничениями». Вот еще типичные разновидности подобных задач.
7. За круглым столом сидят 12 рыцарей. Каждый посажен между теми 2, с которыми он не ладит. Королю Артуру нужно послать отряд из 5 рыцарей, чтобы освободить заколдованную принцессу. Ясно, что в отряде не должно быть враждующих между собой рыцарей. Сколькими способами король Артур может составить такой отряд?
Эта задача близка ключевой задаче 6. Существенное отличие лишь в том, что звери размещались в один ряд, а рыцари расположились по окружности. Но ведь каждый рыцарь может быть либо включен в отряд, либо не включен в него. Приняв один из этих вариантов, можно дальше рассуждать, как в задаче 6.
Пусть рыцарь А не включен в отряд. Тогда из остальных 11 рыцарей надо выбрать 5 так, чтобы никакие 2 из них не сидели рядом. Между 6 оставшимися рыцарями имеется 7 мест, на которых могут находиться те, кого включают в отряд. Порядок выбора по смыслу задачи значения не имеет. Поэтому число возможных способов составить отряд без рыцаря А равно
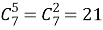
Всего, таким образом, у короля Артура имеется 15+21=36 способов составить отряд для спасения принцессы.
8. Купили 3 книги Тургенева, 4 книги Толстого и по одной книге Пушкина, Лермонтова и Некрасова. Все книги разные. Сколькими способами можно расставить их в ряд так, чтобы книги одного автора стояли вместе?
Будем рассматривать книги одного автора как один предмет. Тогда имеем 5 разных предметов, которые нужно располагать на 5 местах. Это можно сделать
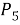
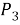
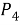
Ответ:
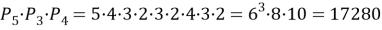
Мама купила 4 яблока, 2 груши и 1 апельсин и решила на протяжении недели давать сыну по одному фрукту. Сколькими способами она может это сделать?
Так как фруктов 7 и дней 7, то ответом будет число перестановок с повторениями с разбивкой 4, 2, 1:
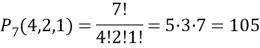
А вот если те же фрукты, но будут выдаваться по одному в течение лишь 5 дней? Тогда придется «повозиться» несколько больше: рассмотреть полную систему событий, т. е. все возможные случаи выбора 5 фруктов из данного набора и в каждом из них подсчитать число распределений по 5 дням (как сделано в первом варианте данной задачи):
Выбор фруктов:
|
Я |
Г |
А |
|
4 |
1 |
0 |
|
4 |
0 |
1 |
|
3 |
2 |
0 |
|
3 |
1 |
1 |
|
2 |
2 |
1 |
Число распределений по дням:
|
|
|
|
|
|
|
|
|
|
Всего же имеется
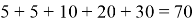
10. Сколько шестизначных чисел, делящихся на 25, можно написать с помощью цифр 0, 1, 2, 3, 4, 5, не повторяя их?
Имеется 6 данных цифр и из них составляют шестизначные комбинации, причем цифры не повторяются. Значит, в каждой комбинации используются все данные элементы, а отличаются эти комбинации только порядком элементов. Следовательно, в данной задаче мы имеем дело с перестановками без повторений.
Вообще на 25 делятся числа, оканчивающиеся на 00, 25, 50, 75. Из них в данной задаче будут встречаться только те, которые оканчиваются на 25 и на 50. Эти числа имеют вид — — — — 25 или — — — — 50, где на месте черточек могут стоять в любом порядке остальные четыре из данных 6 цифр. Их можно распределить
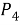
Однако из числа комбинаций, оканчивающихся на 25, надо исключить те, которые начинаются нулем: ведь это не будут шестизначные числа. Комбинации вида 0 — — — 25 будет
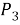
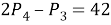
Таким образом, рассмотренные ниже приемы и алгоритмы решения комбинированных задач еще раз показывают широкий диапазон применения и большую роль, которую играют вероятно-статистические задания в общеобразовательной подготовке современного человека. Без минимальной вероятно-статистической грамотности трудно адекватно воспринимать социальную, политическую, экономическую и принимать на ее основе обоснованные решения.
Современные физика, химия, биология, весь комплекс социально-экономических наук построены и развиваются на вероятно-статистической базе и без соответствующей подготовки невозможно полноценное изучение этих дисциплин уже в средней школе.
Литература:
- Ежов И. И., Скороход А. В., Ядренко М. И. Элементы комбинаторики. — М.: Наука, 1977.
- Василенко Ю. К. Начала комбинаторики. Как преподавать их учащимся. — Белгород.: БелГУ, 1993.
- Халамайзер А. Я. Комбинаторика и бином Ньютона. — М.: Просвещение, 1980.