Нахождение численности подмножеств при решении задач на уроках математики



В статье рассмотрены основные подходы к решению комбинаторных задач по нахождению численности подмножеств с определенным набором признаков (свойств).

Ключевые слова: задачи, элементы, множества, подмножества.

Рассмотрим задачи, которые в обобщенном виде сводятся к следующему: данное множество разбито на подмножества по нескольким признакам (свойствам); требуется установить число элементов, обладающих теми или иными признаками (свойствами). Так как эти подмножества пересекаются, т. е. элементы могут иметь несколько из данных признаков, то бывает непросто вычленить сколько именно тех, которые интересуют.

Для выяснения подходов к решению таких задач рассмотрим простой пример. Из 26 учащихся 12 посещают литературный кружок и 10 — физический, причем 4 человека посещают и тот и другой. Сколько учащихся не посещают ни литературный, ни физический кружок?

Для решения задачи нужно общее число учащихся представить как сумму чисел слушателей каждого из кружков и неизвестного числа тех, кто не посещает их. Но будет ли верным равенство ? Конечно, нет. Ведь 4 учащихся, которые посещают оба кружка, мы посчитали дважды — и в числе 12 и в числе 10. А нужно их посчитать, как и остальные, только один раз. Поэтому правильным будет уравнение . Откуда .

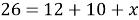
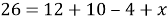
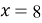
Обозначим число всех учащихся в классе,

и — числа членов соответственно литературного и физического кружков; и — числа тех, кто не посещает соответственно литературный и физические кружки. Тогда будет верным равенство

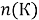
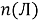
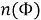
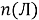
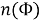
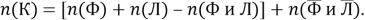
В правой части первые три члена, заключенные в квадратные скобки, выражают число тех учащихся, которые посещают или литературный или физический кружки, т. е. хотя бы один из них. Поэтому можно написать

[1].

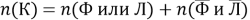
Поставим теперь такой вопрос: сколько учащихся посещают только физический кружок, т. е. посещают физический и не посещают литературный кружок? Очевидно,

.

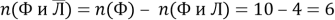
Следует обратить внимание на различный смысл выражений «посещают физический кружок» и «посещают только физический кружок».

В общем случае для разбиения множества по двум признакам и имеем из тех же соображений при сохранении аналогичных обозначений формулу:

(1)

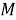
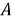
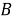
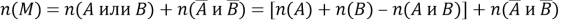
Выражение в квадратных скобках — это число элементов, обладающих хотя бы одним из свойств или .

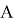
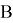
Разумеется, в случае разбиения по двум признакам вовсе не обязательно вводить символику, писать общие формулы. Нетрудно сообразить и без этого. Смысл всей этой «теории» в том, чтобы на простом материале обнаружить общий подход, который можно было бы использовать и в более трудных задачах, где будет больше признаков, по которым производится разбиение.

Формулу (1) можно получить и из теоретико-множественных соображений. То, что обозначено ) — это объединение подмножеств и ; — это их пересечение; — это дополнение до . Формулу можно «увидеть» при помощи диаграмм Эйлера-Венна или доказать аналитически [2]. Однако даже для разбиения по трем признакам первый способ почти теряет свое главное преимущество — наглядность, а аналитическое доказательство становится слишком громоздким.

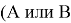
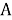
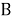
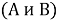
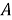
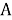
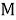
Между тем, чисто логический путь сопоставления численности множества и его подмножеств при увеличении количества признаков лишь удлиняется, но в принципе остается не более сложным.

Теперь обратимся к случаю, когда множество М развивается на подмножества по трем признакам (свойствам). Как и раньше, буквами

, и будем обозначать как сами признаки, так и подмножества элементов, обладающих этими признаками, а символами , и т. п. — число элементов указанного множества.

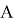
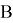
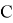
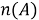
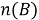
Прежде всего, отметим, что число всех элементов М можно представить как сумму числа элементов, имеющих хотя бы один из данных признаков, и числа элементов, не обладающих ни одним из них.

.

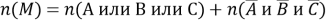
Будем теперь искать выражение для первого слагаемого. Можно ли считать, что

?

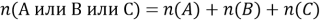
Нет, так как число элементов, обладающих какими-либо двумя из данных трех свойств, мы сосчитали бы дважды — например, в числе и в числе . Значит, число элементов такого вида надо вычесть из общей суммы. Но будет ли уже верным равенство

?

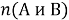
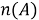
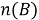
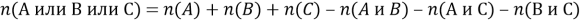
Еще нет, так как могут быть элементы, обладающие всеми тремя признаками. Их число мы трижды взяли со знаком и трижды со знаком , т. е. не прибавили ни разу. А один раз это сделать надо. Значит, чтобы последнее равенство стало верным, надо к его правой части прибавить . Окончательно получаем формулу

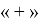
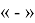
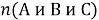
(2)

Отметим, что число элементов, обладающих только одним признаком, например,

можно найти по формуле:

(3)

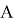
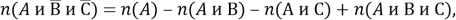
к которой легко прийти аналогичным рассуждением.

Наконец, очевидная зависимость

(4)

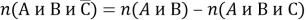
дает выражение для числа элементов, обладающих признаками и , но не обладающих признаком .

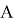
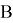
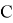
Рассмотрим типичные задачи с разбиением по трем признакам.

Пример 1. Каждая из 30 невест красива, воспитана или умна. В том числе воспитанных 21, красивых 18, умных 15, красивых и воспитанных 11, умных и воспитанных 9, умных и красивых 7. Сколько невест обладают всеми этими качествами?

Введя соответствующие обозначения и учитывая, что по условию задачи число невест, не обладающих ни одним из названных качеств, равно нулю, получим по формуле (2) равенство

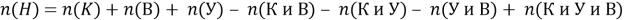
Или, подставив исходные данные, (К и В и У).

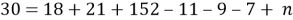
Ответ: 3.

Следующая задача составлена по сюжету, придуманному Льюисом Кэроллом (Чарльзом Джонсоном) — известным английским математиком конца XIX века, автором знаменитой книги «Алиса в стране чудес».

Пример 2. На пиратском корабле все 100 человек экипажа гордятся боевыми увечьями. Среди них 72 одноглазых, 48 одноруких, 25 одноногих, 20 лишились глаза и руки, 18 глаза и ноги, 15 ноги и руки. Сколько одноглазых пиратов имеют обе руки и обе ноги?

Обозначим первый признак — отсутствие глаза — буквой

, отсутствие руки — , отсутствие ноги — . По смыслу задачи . Найти нужно . Согласно формуле (3), . Однако последнее слагаемое здесь нам не известно. Найдем его, подставив исходные данные в формулу (2): . Отсюда . Тогда .

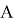
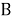
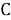
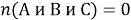
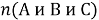
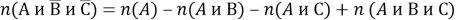
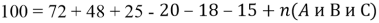
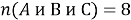
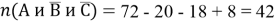
Ответ: 42.

Пример 3. Из 200 абитуриентов задачу по алгебре решили 160 человек, по геометрии — 140, по тригонометрии — 120. При этом задачи по алгебре и геометрии решили 120 абитуриентов, по алгебре и тригонометрии — 100 человек, по геометрии и тригонометрии — 80. А 60 абитуриентов решили все три задачи. Сколько абитуриентов решили хотя бы одну задачу? Сколько не решили ни одной задачи?

По формуле (2) имеем: . Выражение в квадратных скобках — это и есть число абитуриентов, решивших хотя бы одну задачу. Оно равно 180. Не решили ни одной задачи 20 человек.

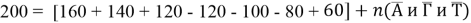
Ответ: 180; 20.

Пример 4. Из 50 студентов 15 посещают спецкурс по математическому анализу, 6 по анализу и геометрии, 5 по алгебре и геометрии, 13 только по алгебре, 2 по всем математическим дисциплинам, 10 предпочитают педагогику. Сколько студентов посещают спецкурс только по геометрии?

Число студентов, посещающих спецкурс только по геометрии, можно выразить в соответствии с формулой (3):

.

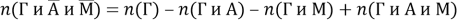
Однако здесь неизвестно , т. е. общее число студентов, посещающих спецкурс по геометрии. Чтобы его найти, напишем формулу (2):

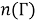
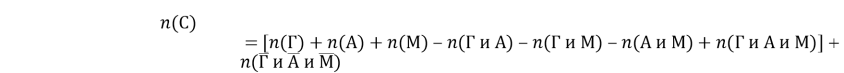
и заметим, что число студентов, посещающих спецкурс только по алгебре, которое известно, равняется (снова формула (3)). Подставив вместо всего этого выражения значение , получим уравнение . Отсюда . Тогда .

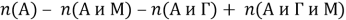
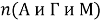
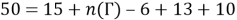
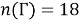
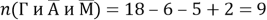
Ответ: 9.

Пример 4. Комнату школьника при домоуправлении регулярно посещают 35 детей. 8 из них занимаются в шахматной секции, 18 в секции настольного тенниса, 12 в секции борьбы. В том числе 5 успевают посещать занятия и по шахматам, и по теннису, 3 — по теннису и борьбе, 2 — по шахматам и борьбе. Остальные — те, кто не увлекается спортом, — посещают кружок рукоделия. Сколько детей занимается в этом кружке?

Согласно формуле (2), число ребят, занимающихся хотя бы в одной спортивной секции, равняется . Значит, кружок рукоделия посещают 7 детей.

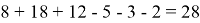
Ответ: 7.

Таким образом, мы рассмотрели общий подход, который можно использовать в решении более трудных задач, где будет больше признаков, по которым производится разбиение.

Литература:

1. Василенко Ю. К. Начала комбинаторики. Как преподавать их учащимся. — Белгород.: БелГУ, 1993.
2. Виленкин Н. В. Индукция. Комбинаторика. — М.: Просвещение, 1976.