Комбинаторика — раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.
Выбором объектов и их расположением в каком-либо порядке люди занимаются во множестве областей человеческой деятельности, например конструктор, разрабатывающий новую модель механизма, ученый-агроном, планирующий распределение сельскохозяйственных культур на нескольких полях, химик, изучающий строение органических молекул, имеющих данный атомный состав.
Такие задачи называют комбинаторными. С ними люди столкнулись в глубокой древности. Несколько тысячелетий назад в Древнем Китае увлекались составлением магических квадратов (квадраты, в которых заданные числа располагаются так, что их сумма по всем горизонталям, вертикалям и главным диагоналям была одинаковой). В Древней Греции подсчитывали число различных комбинаций длинных и коротких слогов в стихотворных размерах, занимались теорией фигурных чисел, изучали фигуры, которые можно составить из частей особым образом разрезанного квадрата, и т. д.
Комбинаторные задачи формировались и во время партий в такие игры, как шашки, шахматы, домино, карты, кости и т. д. (Например, задача об обходе всех полей доски шахматным конем и т. д.)
Еще в глубокой древности существовали азартные игры, которые получили особенное распространение после крестовых походов. Они тоже поспособствовали развитию комбинаторики.
Наибольшее распространение получила игра в кости — два или три кубика с нанесенными на них очками бросали на стол, и ставку брал тот, у кого выпала большая сумма очков. Несмотря на грозные запреты церкви, азартные игры все же развивались.
Эти древние игры не подвергались математическому исследованию довольно долго.
Позже некоторые игроки, которые наиболее часто играли в кости, подметили, что одни суммы очков выпадают часто, а другие — редко. Были составлены таблицы, показывавшие, сколькими способами можно получить то или иное число очков. Но сначала была допущена ошибка — подсчитывалось только число различных сочетаний, дававших данную сумму.
Например, при бросании двух костей сумма 6 получается из сочетаний (1, 5), (2, 4), (3, 3), а сумма 7 — из сочетаний (1, 0), (2, 5), (3, 4). Так как три сочетания были различны в обоих случаях, то напрашивался ошибочный вывод о том, что суммы очков 6, 7 и 8 (также получаемая из трех сочетаний костей) должны выпадать одинаково часто. Но согласно опыту 7 очков выпадает чаще. Сочетание (3, 3) при бросании двух костей может быть получено единственным способом, а сочетание (3, 4) — двумя способами. Именно благодаря этому, сумма 7 выпадает наиболее часто. Таким образом, оказалось, что надо учитывать не только сочетание очков, но и их порядок.
Комбинаторика становится наукой лишь в XVII в. — в период, возникновения теории вероятностей. Чтобы решать теоретико-вероятностные задачи, нужно было уметь подсчитывать число различных комбинаций, подчиненных каким-либо условиям. После первых работ, выполненных в XVI в. итальянскими учеными Дж. Кардано, Н. Тартальей и Г. Галилеем, такие задачи изучали французские математики Б. Паскаль и П. Ферма. Первым рассматривал комбинаторику как самостоятельную ветвь науки немецкий философ и математик Г. Лейбниц, опубликовавший в 1666 г. работу «Об искусстве комбинаторики», в которой впервые употребляется термин «комбинаторный». Замечательные достижения в области комбинаторики принадлежат Л. Эйлеру. Комбинаторными задачами интересовались и математики, занимавшиеся составлением и разгадыванием шифров, изучением древних письменностей. Сейчас комбинаторика находит место во многих областях науки: в биологии, где она применяется для изучения состава белков и ДНК, в химии, механике сложных сооружений и т. д.
Рассмотрим основные типы комбинаторных задач, сформировавшихся в процессе развития комбинаторики. Оказалось, что, несмотря на внешнее различие изучаемых ею вопросов, многие из них схожи математически и сводятся к задачам о конечных множествах и их подмножествах.
Важную область комбинаторики составляет теория перечислений. С ее помощью можно подсчитать число решений различных комбинаторных задач. Также целый ряд комбинаторных задач возникает при разбиении множеств на части: найти число таких разбиений, если число частей равно ![]() ; найти, сколькими способами можно число
; найти, сколькими способами можно число ![]() записать в виде суммы
записать в виде суммы ![]() слагаемых; найти, сколькими способами можно разложить
слагаемых; найти, сколькими способами можно разложить ![]() предметов по
предметов по ![]() ящикам, и т. д.
ящикам, и т. д.
В решении комбинаторных задач часто используют графические методы — изображение разбиений числа на слагаемые в виде точечных диаграмм, так называемые графы (геометрические фигуры, состоящие из точек и соединяющих их отрезков) и т. д. Теория графов стала в наши дни одной из наиболее бурно развивающихся частей комбинаторики. Многие общие теоремы этого раздела математики формулируются на языке графов.
Если заданным условиям удовлетворяют несколько конфигураций, т. е. если комбинаторная задача имеет несколько решений, то может возникнуть вопрос о выборе из них решения, оптимального по тем или иным параметрам. Например, если имеется несколько городов, каждые два из которых соединены мостом, то возникает задача о том, как путешественнику побывать по одному разу в каждом городе, проехав наименьшее расстояние.
Рассмотрим основные правила, называемые основными комбинаторными правилами, на основе которых могут быть выведены другие специальные комбинаторные соотношения.
- Правило птичьих гнезд (принцип Дирихле)
Если имеются n + 1 птицы, которых необходимо разместить в n гнездах, то при любом способе размещения хотя бы в одном гнезде окажется не менее двух птиц.
Задача. В мешке лежат шарики двух разных цветов — черного и белого. Какое наименьшее количество шариков нужно вынуть из мешка, чтобы среди них точно два шарика оказались одного цвета?
Решение.
Понятно, что взяв три шарика, мы обнаружим, что две из них одного цвета. В данном случае роль птиц играют шарики, а роль гнезд — черный и белый цвета.
- Правило умножения.
Множество ![]() , состоящее из всевозможных пар
, состоящее из всевозможных пар ![]() , где элемент
, где элемент ![]() принадлежит множеству
принадлежит множеству ![]() , а элемент
, а элемент ![]() принадлежит множеству
принадлежит множеству ![]() , содержит
, содержит ![]() элементов
элементов
Задача. Сколько всего трехзначных чисел можно составить, используя цифры 7, 4 и 5?
Решение. В данной задаче рассматриваются трехзначные числа, так как цифры в записи этих чисел могут повторяться, то цифру сотен, цифру десятков и цифру единиц можно выбрать тремя способами каждую. Поскольку запись трехзначного числа представляет собой упорядоченный набор из трех элементов, то, согласно правилу произведения, его выбор можно осуществить 27 способами, так как 3 • 3 • 3 = 27.
Задача. Сколько всевозможных трехзначных чисел можно записать, используя цифры 1, 2 и 3 так, чтобы цифры в записи числа не повторялись?
Решение. В задаче рассматриваются размещения без повторений из трех элементов по три, и их число можно подсчитать по формуле:
А ![]() = 3•(3–1)•(3–2) = 3•2•1= 6.
= 3•(3–1)•(3–2) = 3•2•1= 6.
Эти числа таковы: 123, 132, 213, 231, 312, 321.
Заметим, что в данном случае разные числа получаются в результате перестановки цифр.
- Правило сложения
Если множество ![]() состоит из
состоит из ![]() элементов, а множество
элементов, а множество ![]() — из
— из ![]() элементов, причем эти множества не имеют общих элементов, то их объединение
элементов, причем эти множества не имеют общих элементов, то их объединение ![]() , т. е. совокупность всех элементов из
, т. е. совокупность всех элементов из ![]() и
и ![]() , содержит
, содержит ![]() элементов. Правило умножения — основное для определения количества комбинаторных объектов. К нему сводятся различные вспомогательные комбинаторные соотношения и задачи, преобразуемые в семейства задач, решаемых с помощью этого правила.
элементов. Правило умножения — основное для определения количества комбинаторных объектов. К нему сводятся различные вспомогательные комбинаторные соотношения и задачи, преобразуемые в семейства задач, решаемых с помощью этого правила.
Задача. На тарелке лежат 5 груш и 4 персика. Сколькими способами можно выбрать один плод?
Решение. По условию задачи грушу можно выбрать пятью способами, персик — четырьмя. Так как в задаче речь идет о выборе «либо груши, либо персика», то его, согласно правилу суммы, можно осуществить 5 + 4 = 9 способами.
- Размещения с повторениями
Если все элементы x1,x2,…,xk кортежа (x1,x2,…,xk) принадлежат одному и тому же множеству Х, то говорят о кортеже из элементов множества Х.
Пусть множество Х состоит из n элементов.
Кортеж длины k, составленный из элементов множества Х, называется размещением с повторениями из n элементов по k (в кортеже (x1,x2,…,xk) его элементы могут повторяться).
Число всех размещений с повторениями из n элементов по k зависит от n и от k (а не от природы множества Х). Это число обозначается Ank. Формула для его нахождения выводится с помощью правила произведения:
Ank=n*n*…*n=nk (1)
Задача. Сколько трёхзначных чисел может быть составлено из нечётных цифр?
Решение. Х = {1, 3, 5, 7, 9}, n=5.
Трёхзначное число — это кортеж (x1,x2,x3) длины 3, составленный из элементов множества X, причем цифры в числе могут повторяться. Значит, этих чисел будет столько, сколько существует размещений с повторениями из 5 элементов по 3:
A35=53=125.
- Размещения без повторений
Пусть множество Х состоит из n элементов.
Определение. Кортеж длины k, в котором все элементы различны, составленный из элементов множества Х, называется размещением без повторений из n элементов по k (в кортеже (x1,x2,…,xk) элементы не повторяются!).
Так как повторения в кортеже не допускаются, то теперь k должно быть не больше n.
Найдём Akn — число всех размещений без повторений из n элементов по k.
Для выбора элемента x1 имеется n возможностей. После выбора элемента x1, элемент x2 можно выбрать (n-1)-м способом и так далее. Тогда
Akn=n(n-1)(n-2)…(n-(k-1))=n(n-1)(n-2)…(n-k+1) (2)
Задача. Сколько трёхзначных чисел может быть составлено из нечётных цифр так, чтобы цифры в каждом числе не повторялись?
Решение. Х = {1, 3, 5, 7, 9}, n=5.
Трёхзначное число — это кортеж (x1,x2,x3) длины 3 без повторений, составленный из элементов множества X. Значит, этих чисел будет столько, сколько существует размещений без повторений из 5 элементов по 3:
A35=5*4*3=60.
- Сочетания и бином Ньютона.
Всякое k-членное подмножество n-членного множества называется сочетанием из n элементов по k.
Число различных сочетаний из n элементов по k обозначается ![]() .
.
Справедлива формула
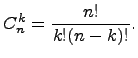
Числа ![]() являются коэффициентами в разложении бинома Ньютона:
являются коэффициентами в разложении бинома Ньютона:
![]()
Задача. Сколькими способами из 10 спортсменов можно отобрать команду из 6 человек?
Решение. Очевидно, команда из 6 человек является 6-членным подмножеством 10-членного множества, т. е. сочетанием из 10 элементов по 6. Следовательно, искомое число способов равно ![]()
Сейчас комбинаторика изучается в школе. Ученики среднего и старшего звена обязательно сталкиваются на уроках математики/алгебры с комбинаторными задачами. Рассмотрим примеры таких задач.
Задача. Сколькими способами можно отправить 8 различных фотографий, используя при этом 5 различных конвертов?
Решение. Решим задачу, используя формулу включений и исключений. Найдем сначала, при скольких способах распределения данные k конвертов оказываются пустыми (а остальные могут быть как пустыми, так и содержать фотографии). В этом случае фотографии кладутся без ограничений в (5-k) конвертов, число таких распределений равно ![]() . Но k конвертов можно выбрать из пяти
. Но k конвертов можно выбрать из пяти ![]() способами. Отсюда, применяя формулу включений и исключений, выводим, что число распределений, при которых ни один конверт не оказывается пустым, равно
способами. Отсюда, применяя формулу включений и исключений, выводим, что число распределений, при которых ни один конверт не оказывается пустым, равно
![]()
Задача. Одноклассники Олег, Вова и Коля дежурят по школе. Сколькими способами классный руководитель может расставить мальчиков по одному на каждом из трех этажей школы?
Решение. Предположим, что Олега назначили дежурить на третьем этаже. Тогда на втором этаже может дежурить Вова или Коля, а на первом — Коля или Вова. Получаем два способа (две комбинации) распределения дежурства (мальчики обозначены первыми буквами их имен).
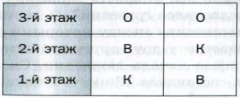
Рис. 1
Пусть теперь дежурным на третьем этаже назначили Вова. Тогда на втором этаже может дежурить Олег или Коля, а на первом — соответственно Коля или Олег. Получаем еще два способа распределения дежурства.
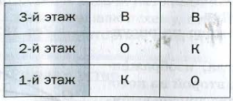
Рис. 2
И наконец, предположим, что дежурной на третьем этаже назначили Колю. Получаем еще два способа распределения.
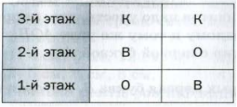
Рис. 3
Таким образом, получилось шесть способов распределения дежурства.
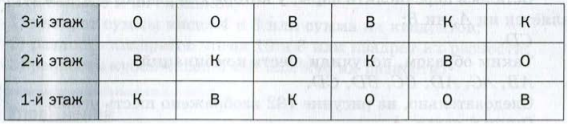
Рис. 4
Итого, 6 способов.
При решении комбинаторных задач важно рассмотреть все случаи. Поэтому процесс перебора лучше делать максимально удобным и наглядным.
Например, решение задачи о распределении дежурства можно проиллюстрировать с помощью такой схемы:
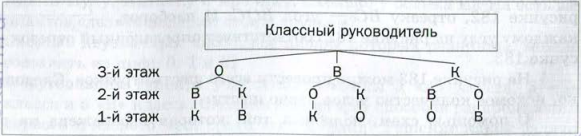
Рис. 5
Эта схема позволяет записать шесть комбинаций, каждая из которых соответствует одному варианту распределения дежурства: ОВК, ОКВ, ВОК, ВКО, КВО, КОВ.
Данная схема напоминает перевернутое дерево. Поэтому ее называют деревом возможных вариантов.
Задача. Сколько углов изображено на рисунке?
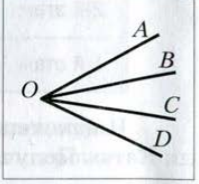
Рис. 6
Решение. Обозначение любого угла, изображенного на рис. 6, состоит из трех букв, второй из которых обязательно является буква O, а две другие выбираются из букв A, B, C, D. Поэтому количество углов равно количеству способов выбрать из букв A, B, C, D две буквы.
При записи всех возможных вариантов необходимо учесть, что комбинации AB и BA соответствуют одному и тому же углу AOB. Вначале перечислим все пары букв с первой A: AB, AC, AD. Теперь перечислим пары, у которых первая буква B, а вторая не является буквой A: BC, BD. Осталось перечислить пары, у которых первая буква C, а второй не является ни A, ни B: CD.
Таким образом, получили шесть комбинаций: AB, AC, AD, BC, BD, CD. Следовательно, на первом рисунке изображено шесть углов.
При решении этой задачи можно воспользоваться такой наглядной схемой. Рассмотрим четыре точки, обозначенные буквами A, B, C, D.
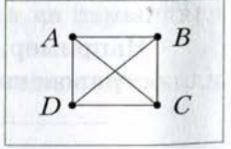
Рис. 7
Тогда количество отрезков, соединяющих каждые две точки, равно количеству углов, изображенных на рис. 6. Например, отрезку AC на рис. 7 соответствует угол AOC на рис. 6, отрезку BC — угол BOC. И наоборот, каждому углу на втором рисунке соответствует определенный отрезок на втором рисунке. На втором рисунке можно провести всего шесть отрезков. Следовательно, искомое количество углов равно шести.
Задача. Сколькими способами из шести предметов (русский язык, литература, алгебра, география, физика, физкультура) можно составить такое расписание, в котором русский язык и литература могут меняться местами?
Решение. Будем рассматривать русский язык и литературу как один предмет, тогда всего предметов будет пять. Число способов, которыми можно составить расписание из пяти предметов, равно Р5=5!. Но в каждой из этих перестановок русский язык и литература могут меняться местами. Поэтому искомое число расписаний вдвое больше. Оно равно 5!*2=240.
Задача. В классе 7 человек имеют пятерку по физике. Сколькими способами можно выбрать из них двоих для участия в олимпиаде по физике?
Решение. Выбираем 2 учащихся из 7, порядок выбора не имеет значения (оба выбранных пойдут на олимпиаду как полностью равноправные); количество способов выбора равно числу сочетаний из 7 по 2: ![]() способ.
способ.
Задача. В одной комнате живут три девушки Оля, Вика и Катя. У них есть 6 флаконов духов, 8 губных помад и 10 лаков для ногтей (все отличаются друг от друга). Сколькими способами девушки могут распределить косметику между собой (так, что каждая получит духи, помаду и лак)?
Решение. Для Оли набор можно набрать 6*8*10=480 способами, для Вики — 5*7*9=315, для Кати — 4*6*8=192. По правилу умножения получаем 480*315*192=29030400 способами.
Задача. Сколькими способами можно рассадить 5 школьников за столом в столовой?
Решение: используем формулу количества перестановок:
![]()
Задача. В классе 16 мальчиков и 12 девочек. Для сценки на праздник в честь 8 марта нужно 4 мальчика и 3 девочки. Сколькими способами можно их выбрать?
Решение. Сначала отдельно выберем 4 мальчика из 16 и 3 девочки из 12. Так как порядок размещения не учитывается, то соответственные соединения — сочетания без повторений. Учитывая необходимость одновременного выбора и мальчиков, и девочек, используем правило произведения. В результате число способов будет вычисляться таким образом:
С164 · С123 = (16!/(4! · 12!)) · (12!/(3! · 9!)) = ((13 · 14 · 15 · 16) / (2 · 3 · 4)) ·((10 · 11 · 12) / (2 · 3)) = 400 400.
Задача. Сколько можно составить разных башенок из семи разноцветных кубиков (только башенки высотой семь кубиков)?
Решение. Всего из 7 разных кубиков можно составить 7*6*...*2*1 = 7! = 5040 упорядоченных последовательностей. Поскольку мы не различаем башенки, отличающиеся друг от друга только поворотом, то это число нужно поделить на 7; кроме того, мы считаем одинаковыми и симметричные башенки, поэтому оставшееся число нужно разделить еще на 2. В итоге получаем 5040 / 14 = 360 разных башенок.
Задача. Даны 2 слова: «абстракционизм» и «многогранность». Коля посчитал, сколько получается слов из слова «многогранность», если вычеркнуть в нем 2 произвольные буквы (получившиеся слова не обязательно осмысленные). Вера сделала то же самое для слова «многогранность». У кого слов получилось больше?
Решение. В данных словах одинаковое количество букв (по 14), поэтому вычеркнуть две буквы из каждого из них можно одинаковым количеством способов. Заметим, что при вычеркивании двух букв из слова «абстракционизм» все полученные слова будут различны, а при вычеркивании букв (мн)ОГ(ог) и (ог)ОГ(ра) из слова «многогранность» получается одно и то же слово «многранность». Поэтому, у Коли получится на одно слово больше. Количество способов выбрать 2 буквы из 14 — это ![]() , именно столько слов будет у Коли, а у Веры будет
, именно столько слов будет у Коли, а у Веры будет ![]() слов. Больше слов у Коли.
слов. Больше слов у Коли.
Задача. Сколькими способами могут быть распределены первое и второе место по итогам поэтического конкурса, если приняло участие в конкурсе 12 человек.
Решение: На первое место претендуют 12 человек, на второе 11 человек. (один займет первое место). По правилу произведения получаем 12 * 11 = 132 способа.
Задача. Выпуклый многоугольник имеет 90 диагоналей. Сколько у него сторон?
Решение: обозначим количество сторон многоугольника через n, вершин у него тоже будет n. Соединим вершины попарно отрезками, которых будет ![]() . Среди этих отрезков будет n сторон, остальные — диагонали. Составим уравнение по условию задачи:
. Среди этих отрезков будет n сторон, остальные — диагонали. Составим уравнение по условию задачи: ![]() . Отсюда получается квадратное уравнение:
. Отсюда получается квадратное уравнение: ![]() , корни которого n1=15, n2= — 12. По смыслу задачи подходит
, корни которого n1=15, n2= — 12. По смыслу задачи подходит ![]() . Ответ: 15 сторон.
. Ответ: 15 сторон.
Задача. Сколько существует трехзначных номеров, не содержащих цифры 2?
Решение. Сначала найдем количество однозначных номеров, отличных от 8. Ясно, что таких номеров девять: 0,1,3,4,5,6,7,8,9. А теперь найдем все двузначные номера, не содержащие двоек. Их можно составить так: взять любой из найденных однозначных номеров и написать после него любую из девяти допустимых цифр. В результате из каждого однозначного номера получится 9 двузначных. А так как двузначных номеров было 9, то получится 9·9 = 92 двузначных номеров.
Итак, существует 92 = 81 двузначный номер без цифры 2. Теперь к каждому из этих номеров можно приписать справа любую из цифр 0,1,3,4,5,6,7,8,9 и получить трехзначный номер, не содержащий цифру 2. При этом получаются все трехзначные номера, удовлетворяющие условию. Итого, 92·9 = 93 = 729 трехзначных номеров без двоек.
Задача. Сколько существует двузначных чисел, в которых цифра десятков и цифра единиц различные и нечетные?
Решение: Поскольку нечетных цифр, употребляемых в качестве единиц и десятков при записи чисел, пять, а именно: 1, 3, 5,7,9, то эта задача сводится к выбору и размещению на две разные позиции двух из пяти различных цифр. Количество этих позиций есть число размещений из 5 по 2: ![]() . Следовательно, искомых чисел 20
. Следовательно, искомых чисел 20
Литература:
- Виленкин Н. Я. Популярная комбинаторика. — М.: Наука, 1975. с.
- Виноградов И. М. Комбинаторный анализ // Математическая энциклопедия. — М.: Советская энциклопедия, 1977. — с.
- Дорофеев Г. В., Суворова С. Б., Бунимович Е. А. Математика 9:Алгебра. Функции. Анализ данных — М.: Дрофа, 2000.
- Савин А. П., Гнеденко Б. В. Комбинаторика // Энциклопедический словарь юного математика. — М.: Педагогика, 1985. — с.
- Типы комбинаторных задач Янеуч!. URL: http://yaneuch.ru/cat_24/tipy-kombinatornyh-zadach/266390.2248940.pagel.html
- Комбинаторика — Юнциклопедия // Юнциклопедия. URL: http://yunc.org/Комбинаторика
- Комбинаторика // Научная библиотека. URL: http://sernam.ru/book_e_math.php?id=55

