Задача наилучшего выбора



В данной работе:

1) Будем измерять вероятность не в процентах, а в долях от единицы. Например, «вероятность равна 43 %» — это то же самое, что «вероятность равна 0,43».

2) Используется «классическое» определение вероятности Р = ,

где m — благоприятное количество исходов, n — общее количество исходов.

Например, в ящике лежат 2 белых шара и 3 черных шара. Какова вероятность достать из ящика белый шар? Р(Б) = = = 0,4.

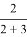
3) Ещё нам понадобится формула «полной вероятности».

Представим себе следующую ситуацию. Иван Царевич стоит на перепутье, перед ним лежит камень, на котором написано: направо пойдёшь, с вероятностью 0,4 утонешь, налево пойдёшь, с вероятностью 0,6 шею сломаешь, а прямо пойдёшь, с вероятностью 0,3 волки загрызут. Иван Царевич решает, что выберет себе дорогу, кинув игральный кубик: если выпадет число 1, то он пойдёт налево, если выпадут числа 2 и 3, то он пойдёт прямо, а выпадут числа 4, 5 и 6, то он пойдёт направо. Спрашивается, с какой вероятностью Иван Царевич погибнет?

Понятно, что вероятность пойти налево равна , пойти прямо — , пойти направо — . Конечно, сумма этих вероятностей равна единице. Погибнуть Иван Царевич может в одном из трёх случаев, в соответствии с количеством направлений. К примеру, вероятность того, что Иван Царевич выберет прямой маршрут и погибнет, равна ·0,3 (важно понимать, что 0,3 — это вероятность Ивана Царевича погибнуть, только если он уже решил пойти прямо, так называемая условная вероятность; но ещё не зная своего будущего выбора, он может посчитать вероятность гибели, состоящую из трёх слагаемых, одно из которых как раз ·0,3). Таким образом, полная вероятность гибели Ивана Царевича равна ·0,3+ ·0,6+ ·0,4 = 0,1 + 0,1 + 0,2 = 0,4, т. е. нужно умножить вероятность каждого случая на соответствующую условную вероятность, а потом результаты сложить.

2. Задача «о разборчивой невесте»

Пусть в некотором царстве, в некотором государстве принцесса решила, что ей пора найти себе жениха. Созвали царевичей и королевичей со всего света, и явилось N (N≥1) претендентов. Про любых двух когда-либо увиденных принцесса может сказать, кто из них лучше. При этом царевичи, для принцессы, все разные. Претенденты входят к принцессе по очереди, по одному, причём их порядок определён случайным образом, т. е. вероятность появления какого-то царевича первым, или десятым, или сотым совершенно одинакова. Принцесса, разумеется, умея их сравнивать, может сказать, что, например, вошедший тридцатым является десятым по качеству, т. е. девять из предыдущих были лучше, а остальные — хуже, и т. д. Цель принцессы — получить самого хорошего жениха. На каждом шаге, т. е. после встречи с каждым из царевичей, она решает, берёт ли она его в мужья. Если берёт, то на этом смотр претендентов заканчивается, они все разъезжаются по домам. Если же принцесса ему отказывает, то царевич, будучи отвергнутым, тут же уезжает домой, потому что все царевичи и королевичи — люди гордые. Показ претендентов на замужество при этом продолжается. Если в конце концов принцесса не получает лучшего, то она уходит в монастырь. Спрашивается, как действовать принцессе, чтобы с наибольшей вероятностью получить лучшего жениха.

Решение

Существует несколько вариантов решения данной задачи, например, подробное школьное решение приведено в [1].

Предоставим альтернативное решение данной задачи.

Определим стратегию принцессы

Можно остановиться на первом же женихе Ж ₁ . Очевидно, что вероятность выбрать при этом самого лучшего равна Р(Ж ₁ ) = (и, значит, стремится к 0 при стремлении N к бесконечности). Тот же результат получится, если остановиться на втором или на третьем и т. д.

На первый взгляд может показаться, что при любом способе выбора вероятность успеха для принцессы будет стремится к 0 при стремлении количества женихов к бесконечности. На самом деле это не так. Допустим для простоты, что число женихов N четно. Предположим, что принцесса пропустила первых женихов, а потом выбирает первого, который окажется лучше всех предыдущих. При такой стратегии принцесса добьется успеха, если самый лучший жених окажется во второй половине последовательности

Ж ₁ , Ж ₂ , Ж ₃ , …, Ж _N , а второй по «качеству» жених — в первой её половине. Вероятность подобной расстановки двух лучших женихов равна

*

= * > 0,25. Где = 1/2 — вероятность того, что самый лучший жених окажется во второй половине последовательности, а — вероятность того, что второй по «качеству» жених окажется в первой половине последовательности, при том что лучший жених своё место уже занял.

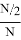
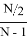
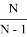
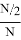
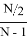
Значит, при четном N для принцессы существует стратегия, обеспечивающая успех с вероятностью более 0,25.

На основании вышесказанного сформулируем стратегию принцессы:

Из общего количества женихов N (N≥1) пропускаем m (m≥0), запоминая среди них наилучшего. И как только появится жених лучше «взятого на заметку», выбираем его.

Рассчитаем вероятность выбрать лучшего жениха при данной стратегии

Данную вероятность будем записывать в виде P _m (N), где N — общее количество женихов, m — количество «пропущенных» женихов.

Для удобства расставим всех женихов по увеличению их «качественных характеристик» и пронумеруем их: Ж ₁ < Ж ₂ < Ж ₃ <...< Ж _N .

Найдем количество перестановок N женихов.

Пусть у нас было 2 перестановки для двух женихов: (Ж ₁ , Ж ₂ ) и (Ж ₂ , Ж ₁ ). Когда добавляется третий жених Ж ₃ , то он может, например, в первой перестановке занять три места: перед Ж ₁ , между Ж ₁ и Ж ₂ и после Ж ₂ . И из перестановки (Ж ₁ , Ж ₂ ) мы получаем три новых перестановки: (Ж ₃ , Ж ₁ , Ж ₂ ); (Ж ₁ , Ж ₃ , Ж ₂ ); (Ж ₁ , Ж ₂ , Ж ₃ ).

Таким образом, количество перестановок увеличивается в три раза 2*3=3!=6. Аналогично, для четырех женихов количество перестановок увеличивается в четыре раза к количеству перестановок трех женихов и становится равно 3!*4=4!=24 и т. д. Можно заметить, что в общем случае количество перестановок женихов равно N! = 1*2*3*...*N.

Рассмотрим всевозможные варианты «ознакомления» с женихами.

1) N=1

Понятно, что принцессе необходимо выбирать данного единственного жениха.

Вероятность добиться успеха принцессы P ₀ (1) = 1.

2) N=2

Общее количество перестановок женихов: 2!=2.

Если принцесса выбирает первого пришедшего жениха:

Ж 1	Ж 2	-
Ж 2	Ж 1	+

Вероятность добиться успеха принцессы P ₀ (2) = 0,5.

Если принцесса пропускает первого и выбирает второго пришедшего жениха:

Ж 1	Ж 2	+
Ж 2	Ж 1	-

Вероятность добиться успеха принцессы P ₁ (2) = 0,5.

Таким образом для принцессы нет разницы как при данном количестве женихов выбирать лучшего, вероятность P ₀ (2) = P ₁ (2) = 1/2 = 0,5.

Здесь и далее «+» означает, что принцесса выиграла, а «-» — проиграла.

3) N=3

Общее количество перестановок женихов: 3!=6.

В случае, когда принцесса выбирает первого жениха или последнего (т.е когда она пропустила (N-1) женихов), вероятность успеха принцессы:

P ₀ (N) = P _N-1 (N) = 1/N.

В нашем случае, P ₀ (3) = P ₂ (3) = 1/3 ≈ 0,333.

Если принцесса пропускает первого жениха:

Ж 1	Ж 2	Ж 3	-
Ж 1	Ж 3	Ж 2	+
Ж 2	Ж 1	Ж 3	+
Ж 2	Ж 3	Ж 1	+
Ж 3	Ж 1	Ж 2	-
Ж 3	Ж 2	Ж 1	-

Вероятность добиться успеха принцессы P ₁ (3) = 3/6 = 0,5.

Таким образом, P ₀ (3) =1/3 ≈ 0,333; P ₁ (3) = 1/2 = 0,5; P ₂ (3) = 1/3 ≈ 0,333.

4) N=4

Общее количество перестановок женихов: 4!=24.

Если принцесса пропускает первого жениха:

Ж1	Ж2	Ж3	Ж4	-	Ж3	Ж2	Ж1	Ж4	+
Ж1	Ж2	Ж4	Ж3	-	Ж3	Ж2	Ж4	Ж1	+
Ж1	Ж3	Ж2	Ж4	-	Ж3	Ж1	Ж2	Ж4	+
Ж1	Ж3	Ж4	Ж2	-	Ж3	Ж1	Ж4	Ж2	+
Ж1	Ж4	Ж2	Ж3	+	Ж3	Ж4	Ж2	Ж1	+
Ж1	Ж4	Ж3	Ж2	+	Ж3	Ж4	Ж1	Ж2	+
Ж2	Ж1	Ж3	Ж4	-	Ж4	Ж2	Ж3	Ж1	-
Ж2	Ж1	Ж4	Ж3	+	Ж4	Ж2	Ж1	Ж3	-
Ж2	Ж3	Ж1	Ж4	-	Ж4	Ж3	Ж2	Ж1	-
Ж2	Ж3	Ж4	Ж1	-	Ж4	Ж3	Ж1	Ж2	-
Ж2	Ж4	Ж1	Ж3	+	Ж4	Ж1	Ж2	Ж3	-
Ж2	Ж4	Ж3	Ж1	+	Ж4	Ж1	Ж3	Ж2	-

Вероятность добиться успеха принцессы P ₁ (4) = 11/24 ≈ 0,458.

Если принцесса пропускает двух первых женихов:

Ж1	Ж2	Ж3	Ж4	-	Ж3	Ж2	Ж1	Ж4	+
Ж1	Ж2	Ж4	Ж3	+	Ж3	Ж2	Ж4	Ж1	+
Ж1	Ж3	Ж2	Ж4	+	Ж3	Ж1	Ж2	Ж4	+
Ж1	Ж3	Ж4	Ж2	+	Ж3	Ж1	Ж4	Ж2	+
Ж1	Ж4	Ж2	Ж3	-	Ж3	Ж4	Ж2	Ж1	-
Ж1	Ж4	Ж3	Ж2	-	Ж3	Ж4	Ж1	Ж2	-
Ж2	Ж1	Ж3	Ж4	-	Ж4	Ж2	Ж3	Ж1	-
Ж2	Ж1	Ж4	Ж3	+	Ж4	Ж2	Ж1	Ж3	-
Ж2	Ж3	Ж1	Ж4	+	Ж4	Ж3	Ж2	Ж1	-
Ж2	Ж3	Ж4	Ж1	+	Ж4	Ж3	Ж1	Ж2	-
Ж2	Ж4	Ж1	Ж3	-	Ж4	Ж1	Ж2	Ж3	-
Ж2	Ж4	Ж3	Ж1	-	Ж4	Ж1	Ж3	Ж2	-

Вероятность добиться успеха принцессы P ₂ (4) = 10/24 ≈ 0,417.

Таким образом, P ₀ (4) = 6/24 = 1/4 = 0,25; P ₁ (4) = 11/24 ≈ 0,458;

P ₂ (4) = 10/24 ≈ 0,417; P ₃ (4) = 6/24 = 1/4 = 0,25.

По полученным данным построим график зависимости вероятности выигрыша принцессы от количества пропущенных женихов для N = 4 (рис. 1)

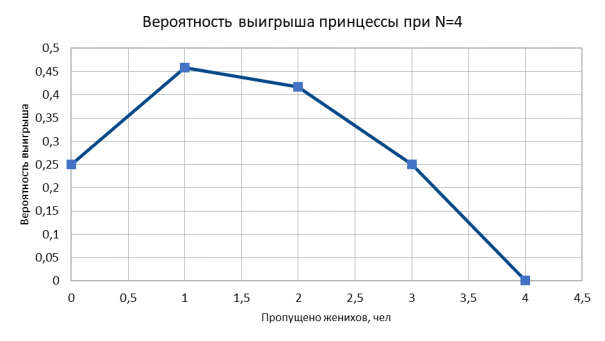
Рис. 1

5) N=5

Общее количество перестановок женихов: 5!=120.

Из-за большого количества вариантов таблицы перестановок женихов приводить не будем, но при желании каждый может их воспроизвести.

Если принцесса выбирает первого жениха: P ₀ (5) = 24/120 = 1/5 = 0,2

Если принцесса пропускает первого жениха: P ₁ (5) = 50/120 ≈ 0,417

Если принцесса пропускает двух первых женихов: P ₂ (5) = 52/120 ≈ 0,433

Если принцесса пропускает трёх первых женихов: P ₃ (5) = 42/120 = 0,35

Если принцесса выбирает последнего жениха: P ₄ (5) = 24/120 = 1/5 = 0,2

По полученным данным построим график зависимости вероятности выигрыша принцессы от количества пропущенных женихов для N = 5 (рис. 2)

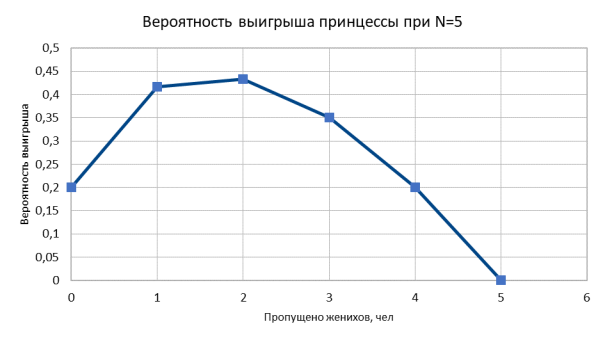
Рис. 2

Решим задачу в общем виде.

Обозначим: самого лучшего претендента — Ж _N , символами «*» — пропущенных претендентов, а символами «О» — остальных претендентов.

Пусть принцесса пропустила m претендентов и начинает выбирать себе мужа.

Если возникла ситуация **...*Ж _N ОО...О, то принцесса выиграла. Вероятность данного события .

Если возникла ситуация **...*ОЖ _N О...О, то вероятность победы принцессы

, где

— вероятность попасть Ж _N на (m+2) место, а — вероятность того, что из (m+1) претендентов расположенных на 1,2,…,m+1 местах самый лучший из них расположен на любом из 1,2,…, m мест.

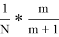
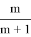
Аналогично, если возникла ситуация **...*ООЖ _N О...О, то вероятность победы принцессы и т. д.

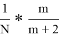
Окончательно, если возникла ситуация **...*ОО...ОЖ _N , то вероятность победы принцессы .

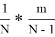
Тогда, вероятность того, что принцесса выберет наилучшего мужа:

P _m (N)= + + + … +

.

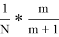
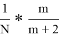
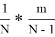
Преобразуем данное выражение:

P _m (N)= *(1+m*( + + … + )).

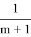
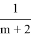
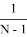
Или

P _m (N)= (1)

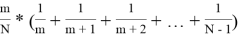
Вычислим количество пропущенных женихов m (для фиксированного N) при котором вероятность выигрыша принцессы максимальна.

Имеем:

P _m (N) > P _m-1 (N) (2)

P _m (N) > P _m+1 (N). (3)

Из (2) получаем

>

>

>

> 1

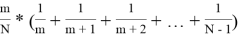
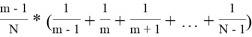
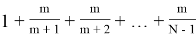
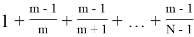
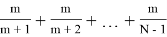
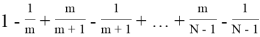
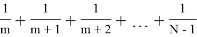
Из (3) получаем

>

>

>

>

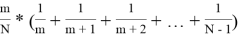
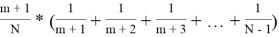
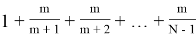
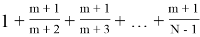
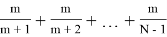
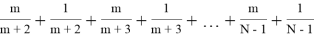
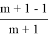
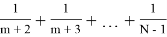
1>

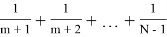
Объединяя два неравенства получим условие нахождения m:

+

+ + … + > 1 > + + … + (4)

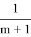
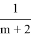
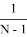
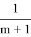
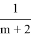
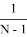
Применяя формулы (1) и (4) с использованием программы Microsoft Excel заполним таблицу:

N	1	2	3	4	5	6	7	8	9	10
m	0	0	1	1	2	2	2	3	3	3
P m (N)	1	0,500	0,500	0,458	0,433	0,428	0,414	0.410	0,406	0,399
N	11	12	13	14	15	16	17	18	19	20
m	4	4	5	5	5	6	6	6	7	7
P m (N)	0,398	0,396	0,392	0,392	0,389	0,388	0,387	0,385	0,385	0,384
N	25	30	35	40	45	50	60	70	80	90
m	9	11	13	15	16	18	22	26	29	33
P m (N)	0,381	0,379	0,377	0,376	0,375	0,374	0,373	0,372	0,372	0,371
N	100	200	300	400	500	600	700	800	900	1000
m	37	73	110	147	184	221	257	294	331	368
P m (N)	0,371	0,369	0,369	0,369	0,369	0,368	0,368	0,368	0,368	0,368

По полученным данным строим графики зависимости вероятности выигрыша принцессы от общего количества женихов (при N=20 (рис. 3) и N=1000 (рис. 4)) и количество «пропущенных» женихов m от общего количества женихов (при N=20 (рис. 5) и N=1000 (рис. 6)). Где m — это то количество пропущенных женихов при котором вероятность выигрыша принцессы P _m (N) максимальная.

Как можно заметить, вероятность выигрыша принцессы при увеличении N стремится к величине 0,368 (рис. 4).

График количества «пропущенных» женихов m от общего количества женихов состоит из «ступенек» (рис. 5). При больших N (рис. 6) данный график заменим прямой линией.

Тогда имеем N = k*m+b, где k и b — коэффициенты.

Из рис. 6 получаем: b = 0; k = 1/0,368 ≈ 2,72.

Окончательно, N ≈ 2,72*m или m ≈ 0,368*N.

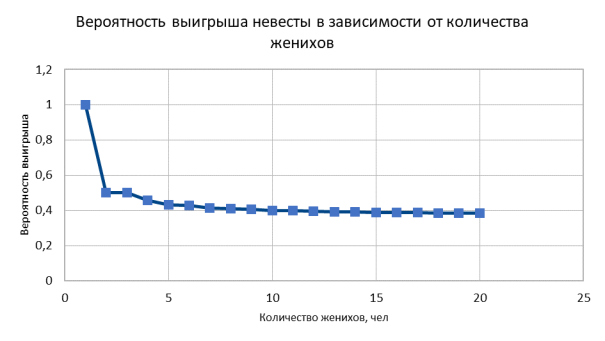
Рис. 3

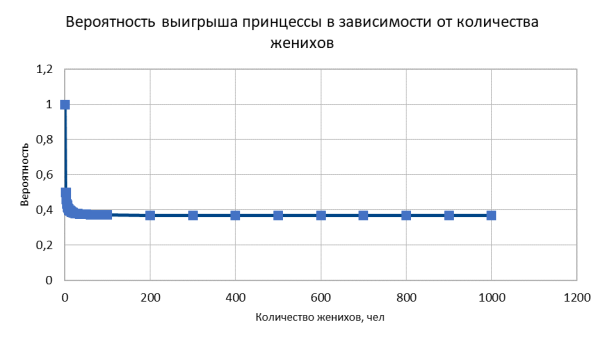
Рис. 4

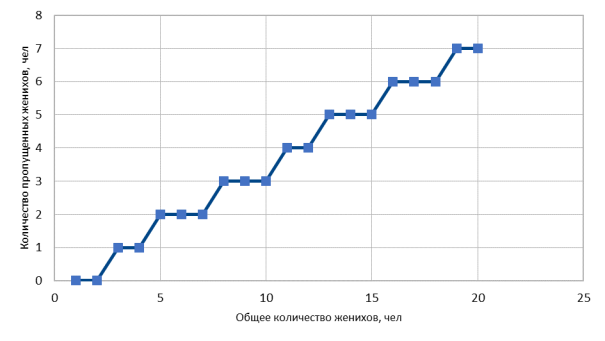
Рис. 5

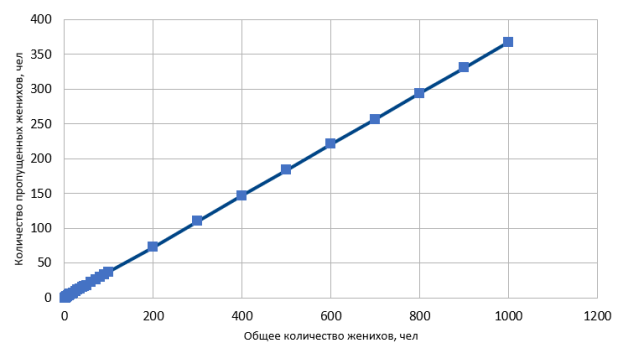
Рис.6

Таким образом, ответ на поставленную вначале задачу выглядит так: принцесса должна сначала пропустить [0,368*N] женихов (где [x] — целая часть числа), только запоминая их для будущего сравнения, а дальше она должна брать в мужья первого же, который обладает тем свойством, что он лучше всех своих предшественников. При этом вероятность получить в конце концов самого лучшего жениха из всех N претендентов равна примерно 0,368.

3. Задачи для размышления

В процессе выполнения данной работы возникли идеи нескольких задач, возможность решения которых школьными методами вызывает определенные трудности. Но желающие могут «попытать счастье».

3.1. Задача «о не очень разборчивой невесте»

Предположим, что принцесса не настолько привередлива, чтобы требовать только самого лучшего жениха, а её устроит и второй по качеству или, например, один из трёх лучших. В более общем случае она ставит своей целью выбор одного из k лучших женихов (k — фиксированное заранее число), при этом какой именно из этих k женихов ей достанется — безразлично.

Спрашивается, как действовать принцессе, чтобы с наибольшей вероятностью получить одного из k лучших женихов.

3.2. Задача «о разборчивой невесте и забывчивых женихах»

В данной задаче предположим, что принцесса отправила приглашение N претендентам, но, к сожалению, царевичи люди очень занятые, один уехал на войну, второй бьется с драконом и ему не до женитьбы, а третий и вовсе забыл.

В общем принцесса не представляет сколько женихов откликнется на её предложение (возможно приедут все приглашенные), единственно она знает, что вероятность приезда k женихов (где k=1,2,..,N) составляет P(k) = 1/N или другой наперёд известный закон распределения вероятности.

Спрашивается, как действовать принцессе, чтобы с наибольшей вероятностью получить, из почтивших её своим вниманием, лучшего жениха.

3.3. Задача «о привередливой невесте»

Предположим, что принцесса настолько привередлива, чтобы требовать не самого лучшего жениха, а только второго по качеству или, например, только третьего. В более общем случае она ставит своей целью выбор k-ого по качеству жениха (k — фиксированное заранее число), при этом важно, чтобы ей достался именно k-ый по качеству жених.

Спрашивается, как действовать принцессе, чтобы с наибольшей вероятностью получить k-ого жениха.

3.4 Задача «о разборчивой невесте и мудром короле»

В данной задаче предположим, что когда принцесса делает свой выбор, старый и мудрый король (её отец) с «высоты» прожитых своих лет может подсказать дочери k раз (k — фиксированное заранее число), что данный претендент не является лучшим женихом, если это действительно так. И принцесса, как послушная дочь, меняет свой выбор.

Спрашивается, как действовать принцессе и с какой вероятностью она получит лучшего жениха.

Литература:

1. Гусейн-Заде С. М. Разборчивая невеста. М.: МЦНМО, 2002. https://www.mccme.ru/free-books/mmmf-lectures/book.25.pdf