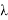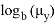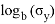Проверка гипотезы о нормальном распределении логарифмической доходности по критерию Шапиро — Уилка

Актуальность и цели. В данной работе производится анализ логарифмических доходностей акций, входящих в состав российского IT сектора. Предполагается, что дневная логарифмическая доходность распределена по нормальному закону. Цель работы — проверить гипотезу о нормальном распределении дневных логарифмических доходностей на реальных данных. С экономической точки зрения задача исследования — определить таймфреймы и промежутки времени, на которых логарифмические доходности будут иметь нормальное распределения, а также те, на которых условия не выполняются. Помимо этого, необходимо выяснить, как повлияло изменение цен акций в 2022 года на сектор информационных технологий. В дальнейшем эту информацию можно использовать для прогнозирования цен акций исследуемых компаний. Для проверки используется критерий Шапиро — Уилка, являющийся одним из наиболее эффективных критериев. После этого проверяется гипотеза на реальных данных и вычисляется процент проверок, в которых гипотеза будет приниматься при уровне значимости в 5 % и 1 %.

Временной отрезок для рассмотрения: 01.01.2022–31.12.2022

Ключевые слова : логарифмическая доходность, уровень значимости, нормальное распределение, проверка гипотезы

Введение

Информационный сектор играет важную роль в экономике России и является одной из самых быстро развивающихся отраслей. Он включает в себя производство и распространение информационных товаров и услуг, таких как программное обеспечение, интернет-сервисы, мультимедиа-контент и многое другое. Информационные технологии также широко применяются в других отраслях, таких как финансы, производство, здравоохранение, транспорт и телекоммуникации.

Вклад информационного сектора в экономику России растет из года в год. Согласно отчету Аналитического центра при Правительстве Российской Федерации, в 2020 году доля информационных технологий в ВВП России составила 4,5 %, а объем рынка информационных технологий оценивался в 3,4 трлн рублей.

Этот сектор является ключевым для развития экономики России, поскольку способствует созданию новых рабочих мест, привлечению инвестиций, улучшению качества жизни и повышению конкурентоспособности страны в мировом рынке. Более того, информационные технологии могут существенно повысить эффективность работы государственных органов и бизнеса, что в свою очередь ведет к увеличению производительности и экономического роста.

С экономической точки зрения, оценивается изменение цен акций в 2022 году в сектор информационных технологий. Определение на каких промежутках логарифмические доходности имели нормальное распределение позволит спрогнозировать дальнейшее изменение в данном секторе.

Основная часть

Для проверки критерия были взяты акции компаний, которые входят в сектор информационных технологий, а именно:

HHRU — HeadHunter

VKCO — Вконтакте

OZON — Озон

MTSS — МТС

POSI — Positive Technologies

SFTL — Softline

Для того чтобы использовать эти данные для проверки нормальности по критерию Шапиро — Уилка, необходимо провести их предварительный анализ. В первую очередь, посчитаем логарифмические доходности акций.

1 Теоретическая справка по проверке гипотез

1.1 Статистическая проверка гипотез

Статистическая гипотеза — это любое утверждение о виде или параметрах генерального распределения. Гипотезу называют основной и обозначают

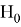
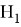
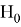
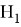
Пусть - некоторое подмножество . В этом случае правило, в соответствии с которым H ₀ отвергается, если выборка , и принимается, если , называется статистическим критерием с критической областью К. Так как и являются гипотезами, которые исключают друг друга, принятие

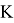
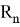
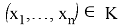
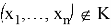
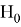
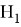
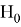
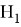
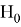
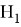
Использование статистического критерия может привести к ошибкам двух типов, которые приведены в таблице 1:

1. Ошибка первого рода заключается в том, что отвергается верная гипотеза .
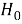
2. Ошибка второго рода заключается в том, что отвергается верная гипотеза .

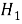
При этом, уровнем значимости критерия называется вероятность ошибки первого рода и обозначается . Вероятность ошибки второго рода обозначается , а величина — это мощность критерия.

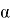
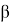
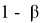
Таблица 1

Гипотезы

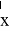
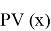
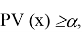
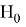
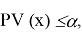
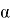
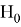
Предполагается, что Р-значение уже каким-либо способом найдено. В этом случае решение о принятии или отклонении

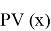
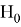
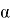
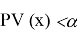
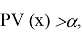
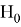
Рассматривается отдельно случай В этом случае где c(- непрерывная убывающая функция, и для имеет место равенство , означающее, что принимается. Отсюда уже легко получить широко применяемую формулу:

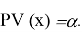
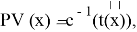
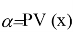
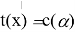
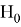
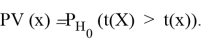
1.2 Критерий Шапиро — Уилка

В данной работе используется критерий Шапиро — Уилка. Он используется для проверки гипотезы H ₀ : «случайная величина X распределена нормально».

Критерий Шапиро — Уилка основан на анализе линейной комбинации разностей порядковых статистик. Критерий применяется при объемах выборки от 3 ≤ n ≤ 50, так как табулированы константы, необходимые для вычисления статистики критерия и аппроксимации P-значения.

Пусть имеется выборка Статистика вычисляется по формулам:

, где , ,

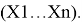
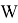
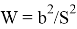
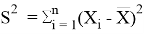
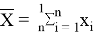
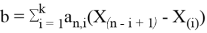
Значение k в последней формуле определяется следующим образом:

, если n — четное

, если n — нечетное

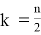
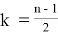
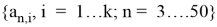
Нормальная аппроксимаций используется для вычисления реально достигнутого уровня значимости:

, где

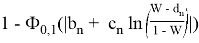
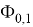
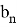
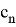
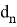
Если , то нулевая гипотеза нормальности распределения отклоняется на уровне значимости .

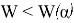
Ж. П. Ройстон предложил другой способ вычисления P-значения для n вплоть до 2000: и , где z — стандартная нормальная случайная величина, а и ее матожидание и среднеквадратичное отклонение. Данная формула будет использована для нахождения уровня значимости и p — значений. Чтобы найти уровень значимости для конкретного

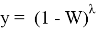
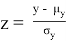
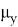
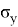
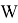
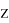
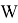
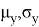
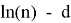
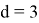
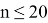
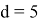
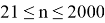
Таблица 2

Коэффициенты

В данном разделе анализируются данные логарифмической доходности и применяется к ним критерий Шапиро — Уилка. Далее выбираются данные, в которых гипотеза принимается при 5 % и 1 % уровнях значимости. Строиться ряд гистограмм и делаются выводы.

Для удобства использования уровни значимости будут отмечаться следующим образом: 5 % — 0.12 , 1 % — 0.02

2.1 Гипотеза о нормальности распределения логарифмической доходности для периода в 6 месяцев

Далее анализируются данные на промежутке в 6 месяцев. Результаты приведены в таблице 3.

Таблица 3

Проверка критерия на промежутке в 6 месяцев

Из таблицы следует, что на временных промежутках в 6 месяцев p-значение выше 1 % не имела ни одна компания.

2.2 Гипотеза о нормальности распределения логарифмической доходности для периода в 3 месяца

Проверяются данные на промежутке в 3 месяца. Результаты приведены в таблице 4.

Таблица 4

Из таблиц видно, что с уменьшением исследуемого периода, возрастает количество логарифмических доходностей, которые имеют нормальное распределение.

Таблица 5

Итоговые результаты

Итоговые результаты показывают, что логарифмические доходности имели нормальное распределение лишь на промежутке в 3 месяца. Также следует отметить, что это было характерно только для 2 и 4 квартала.

Заключение

В данной работе проводился анализ логарифмических доходностей акций, входящих в состав сектора информационных технологий. В ходе работы были получены следующие результаты:

На промежутке в 1 год с таймфреймом 1 день не нашлось значений, которые имеют p-значение выше 5 %. На промежутке в 6 месяцев с таймфреймом 1 день количество значений, которые имеют нормальное распределение не увеличилось.

На промежутке в 3 месяца с таймфреймом 1 день, лишь 25 процентов акций имеют нормальное распределение. При этом, нормальное распределение акций встречалось только во втором и четвертом квартале.

Можно сделать вывод, что использование критерия Шапиро — Уилка для проверки нормальности распределения не позволяет выявить закономерности для предсказания будущих цен акций.

Литература:

2. В. Е. Гмурман Теория вероятностей и математическая статистика, Юрайт, 2011

3. Фадеева Л. Н. Лебедев А. В. Теория вероятностей и математическая статистика, Эксмо, 2010

4. J. P. Royston, Extension of Shapiro and Wilk's W Test for Normality to Large Samples, p. 118

5. Shapiro S. S., Wilk M. B. An analysis of variance test for normality (complete samples) Biometrika, 52 No. 3/4. (Dec., 1965), pp. 591–611