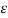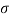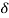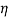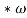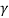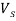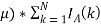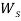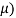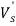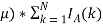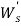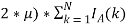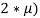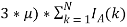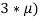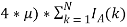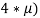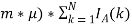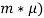Разработка математической модели финансовых рынков на основе Гауссовского случайного блуждания



В статье автор пытается создать концепт новой математической модели эконометрических взаимодействий на финансовых рынках. В основу модели заложено случайное блуждание с размером шага, который варьируется в зависимости от нормального распределения. Формат торгов представлен в виде аукциона с разными показателями рынка, в основе моделирования которого лежит Гауссовское случайное блуждание. Переход состояния рынка осуществляется с помощью матрицы вероятностей перехода.

Ключевые слова: математическая модель, моделирование, финансовые рынки, вероятность.

В современном IT мире уже существуют закрытые тестирующие системы для участников фондовых рынков (дилеров, брокеров, маркетмейкеров и т. д.), созданные для решения задач скальпинга и трейдинга. Главной задачей таких систем является проверка стратегий принятия решений участниками рынка, что уменьшает некоторые операционных риски. В реализациях используются детерминированные лонгитюдные данные, то есть многомерные данные, которые получаются серией наблюдений за конкретный период времени для одних и тех же компаний. Другими словами, участники рынка тестируют алгоритмы и стратегии на одних и тех же фондовых рынках. Предлагается первичное, обобщенное тестирование на предлагаемой математической модели. Это позволит отсечь многие алгоритмы с точностью предсказания меньшей, чем методом средних арифметических и медиан рангов [1], отличающийся своей простотой и популярностью в оценке эффективности предсказаний.

В аукционе учувствуют N участников, которые выполняют действия реальных участников рынка, таких как брокер, дилер, маркетмейкер и тд. Каждый участник имеет заданный номер 1 ≤ k ≤ N. Каждый участник с номером k имеет начальный капитал в размере _k единиц валюты, Q _k единиц сырья, P _k единиц продукции и F _k производств. _k , Q _k , P _k , F _k являются случайными величинами. Моделирование идет циклами — минимальными колебаниями курса на рынке.

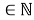
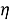
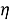
На каждом цикле участники производят на своих производствах продукцию из сырья. Сырье увеличивается на каждом цикле и представляет из себя случайный процесс:

Q _{k c} = Q _k + E _k — , c

_— порядковый номер цикла, E _k = const — количество нового сырья, — случайная величина, определяющая издержки.

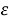
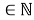
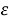
Одно производство может произвести одну единицу продукции, потратив одну единицу сырья и заплатив издержки в виде константной величины = const для каждого производства, цена издержки определяется до старта моделирования. Производство продукции так же является случайным процессом:

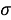
P _{k c} = P _k + A _k — , A _k = const — количество новой продукции, — случайная величина, определяющая издержки.

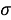
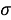
Если у участника недостаточно сырья, производств или валюты, то производство не будет удовлетворено.

На каждом цикле участник имеет возможность сделать заявку на строительство производства. Цена строительства является константной величиной = const, определяющаяся до старта моделирования. Строительство производства является случайным процессом:

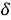
F _{k c} = F _k + B _k —

, B _k = const — количество новых производств, — случайная величина, определяющая издержки.

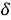
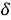
По итогам цикла с каждого участника списывается комиссия рынка — случайная величина, определяемая уровнем рынка и константная комиссия за каждую единицу сырья и производства.

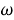
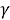
Сведем правила рынка для участников в таблице 1.

Таблица 1

Правила рынка

	Количество	Увеличение	Издержки
Сырье	Q k	E k
Продукция	P k	A k
Производство	F k	B k
Валюта	k	?	Q k + P k +

Каждый цикл рынок проводит аукционы по продаже и закупке выбранной продукции участников, выбирая оптимальное предложение. Единичное предложение определяется по формуле:

L _k = _k

_k , L _k , _{k —} количество единиц продукции, _{k —} установленная участником цена продукции

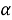
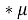
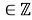
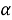
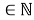
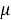
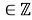
В свою очередь предложение равно:

_k , где x — количество предложений участника во время цикла

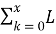
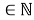
Оптимальное предложение на продажу в свою очередь определяется так:

S _p = max( _k ), 0 p N

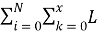
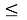
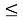
Таким образом, рынок приобретет все единицы продукции у участника с оптимальным предложением, а затем определит чье предложение будет удовлетворено следующим. Аналогично задается оптимальное предложение на покупку:

B _p = min( _k ), 0 p N

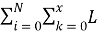
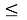
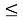
Рынок продолжит удовлетворять предложения участников до тех пор, пока количество продукции, которое закупает(продает) рынок больше нуля.

Пример. Пусть участник k ₁ подал заявку на продажу

₁ единиц, цена _{min 1} цена _max , а участники k ₂ и k ₃ подали заявки на продажу ₂ единиц, цена _{min 2} цена _max и ₃ = ₂ , _{3 =}

₂ соответственно, где цена _min и цена _max задаются рынком на каждом уровне состояния. цена _min , цена _max . При этом ₁ , ₂ , ₃ количества единиц продукции, которое закупает рынок на данном цикле, _{1 * 1} , _{2 * 2} ,

_{1 * 1} , _{3 * 3} . Тогда рынок купит всю продукцию у участника k ₁ , а затем у участников k ₂ и k ₃ . Если продукции, закупаемой рынком, меньше, чем в сумме у участников k ₂ и k ₃ , то рынок удовлетворит полностью или частично предложение одного из участников, выбрав его случайным образом, например, с помощью формулы Фишера — Йейтса [2].

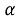
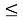
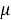
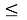
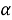
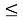
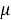
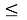
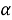
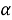
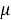
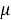
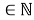
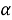
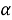
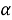
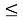
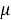
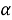
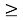
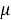
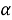
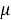
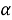
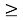
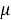
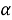
По итогам некоторого количества циклов G ≥ 0, участник, которому не хватило количества валюты на покрытие издержек, объявляется банкротом и выходит из моделирования.

Обстановка на рынке может находиться на одном из m уровней. В зависимости от уровня определяются предложения рынка на покупку и продажу продукции у участников. Определяется и цена _min , цена _max за единицу продукции. Значения определяются по таблице 2 уровней состояния рынка с помощью случайного блуждания [3].

Таблица 2

Уровни состояния рынка

Ур	Покупка		Продажа
	Кол - во	цена min	Кол-во	цена max
1	( +	( +	( +	( +
2	( +	( +	( +	( +
3	( +	( +	( +	( +
4	( +	( +	( +	( +
…	…	…	…	…
m	( +	( +	( +	( +

В данном случае размер шага переходов на другой уровень является обратным кумулятивным нормальным распределением , где 0

z 1 и является равномерно распределенным случайным числом, а и это среднее и стандартное отклонения нормального распределения, соответственно. Если это начальное значение случайного блуждания, то ожидаемое значение после m шагов равно + m . — индикатор принадлежности игрока с номером k к числу игроков, которые еще не стали банкротами. По определению . , ,

, — соответствующие начальные значения случайного блуждания.

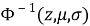
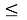
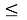
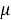
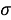
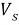
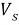
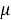
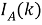
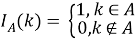
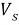
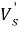
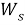
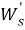
В начале моделирования уровень определяется случайным образом. Уровень для каждого следующего цикла определяется из предыдущего случайным образом в соответствии с матрицей вероятностей перехода. Отметим, что для задания матрицы перехода возможно и использование одномерного дискретного случайного блуждания — цепи Маркова [4]

, где

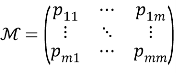
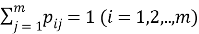
Моделирование происходит до тех пор, пока не останется единственный участник. Аукцион объявляет закрытие и начинает новое моделирование с новыми участниками.

Литература:

1. Метод средних арифметических. URL: https://clck.ru/JRFy5

2. Тасирование Фишера — Йейтса. URL: https://clck.ru/FFQy5

3. Случайное блуждание // Гауссовское случайное блуждание. URL: https://clck.ru/Z5zQJ

4. Случайное блуждание // как цепь Маркова. URL: https://clck.ru/Z5zNe