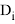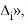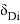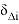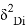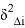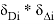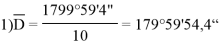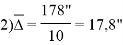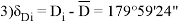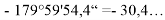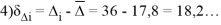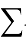Изучение реальных процессов обычно предполагает наблюдение за целым рядом случайных величин. Исключительный интерес для широкого класса задач представляет обнаружение взаимных связей между двумя и более случайными величинами. Например, существует ли связь между курением и ожидаемой продолжительностью жизни или между умственными способностями и успеваемостью. В инженерных применениях такие задачи обычно сводятся к установлению связи между некоторым предполагаемым возбуждением и наблюдаемым откликом изучаемой физической системы. Корреляционно-регрессионный анализ подразумевает всестороннее исследование корреляционных связей, в том числе нахождения уравнении регрессии, измерение тесноты связи и определения ее направления, а также определение возможных ошибок.
Ключевые слова: корреляция, регрессия, триангуляция, критерий Фишера.
Введение
В связи с научно-техническим прогрессом, начавшимся в середине ХХ века, отмечается активное применение математических методов исследования во всех без исключения науках. Математическое мышление стало очень важным для ученых всех специальностей, в том числе и для маркшейдеров, геодезистов.
Развитие новых разделов математики, специально предназначенных для изучения сложных динамических систем, и накопленный опыт их использования в геологии облегчили внедрение математических методов в маркшейдерское дело.
До сих пор еще в маркшейдерском деле наиболее широко используются вероятностно-статистические методы, используемые для анализа протоколов геодезических и геолого-маркшейдерских измерений, встречающихся при развитии сетей обоснования, маркшейдерских съемках, исследовании инструментов и приборов, обработке геолого-разведочных данных, при геометризации месторождений полезных ископаемых. Целью данной работы является рассмотрения применения математических методов исследования статистических данных для решения вопросов горного дела.
Понятие о статистических связях
Существует две формы зависимости между величинами Х и Y: функциональная и статистическая или вероятностная.
— Функциональной зависимостью между двумя величинами Х и Y называют такую зависимость, при которой каждым значениям Х соответствуют значения Y, которые можно точно указать.
— Статистической зависимостью между величинами Х и Y называют такую зависимость, при которой каждому значению Х соответствует распределение значений Y, изменяющееся вместе с изменением Х. Частным случаем статистической связи является прямолинейная корреляционная зависимость, при которой с изменением Х изменяется математическое ожидание Y по линейному закону.
— В математической статистике взаимосвязь явлений и их признаков изучают методом корреляции. Под корреляцией понимают такую связь между случайными величинами, при которой одна случайная величина реагирует на изменения другой. Теснота линейной корреляционной связи между двумя величинами Х и Y характеризуется коэффициентом корреляции
Свойства коэффициента корреляции:
— коэффициент корреляции изменяется в пределах: –1≤ r ≤+1;
— в случае, когда r <0 говорят о отрицательной корреляции, при r >0 говорят о положительной;
— если r =±1, то имеет место функциональная прямолинейная связь;
— если r =0, то между Х и Y прямолинейная корреляционная связь отсутствует. Оценка коэффициента корреляции определяется по формуле:
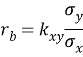
— Положительная корреляция между случайными величинами характеризует такую вероятностную зависимость между ними, когда при возрастании одной другая будет в среднем возрастать.
— Отрицательная корреляция характеризует такую зависимость, когда при возрастании одной из них другая в среднем будет убывать.
Для оценки надёжности коэффициента корреляции r при большом числе измерений ( n >50) применяют критерий Романовского:
Для оценки надёжности r* при малом числе измерений ( n <50)применяют критерий Фишера.
Задача 1. Втабл. 1 приведены результаты измерений триангуляции D i и абсолютные значения невязок Δ i (в секундах) их сопровождающих. Вычислить коэффициент корреляции; с вероятностью 0,90 оценить его надёжность и составить уравнение регрессии Δ на D .
Решение . Вычисление необходимых сумм, поместим в таблице ниже.
|
№ |
|
|
|
|
|
|
|
Примечания |
|
1 |
179°59'24" |
36" |
-30,4 |
18,2 |
924,16 |
331,24 |
-553,28 |
|
|
2 |
179°59'35" |
25" |
-19,4 |
7,2 |
376,36 |
51,84 |
-139,68 | |
|
3 |
179°59'49" |
11" |
-5,4 |
-6,8 |
29,16 |
46,24 |
36,72 | |
|
4 |
180°00'14" |
14" |
-40,4 |
-3,8 |
1632,16 |
14,44 |
153,52 | |
|
5 |
179°59'56" |
4" |
1,6 |
-13,8 |
2,56 |
190,44 |
-22,08 | |
|
6 |
180°00'26" |
26" |
31,6 |
8,2 |
998,56 |
67,24 |
259,12 | |
|
7 |
180°00'3" |
3" |
8,6 |
-14,8 |
73,96 |
219,04 |
-127,28 | |
|
8 |
179°59'29" |
31" |
-25,4 |
1 3 ,2 |
645,16 |
174,24 |
-3 35 , 2 8 | |
|
9 |
179°59'50" |
10" |
-4,4 |
-7,8 |
19,36 |
60,84 |
34,32 | |
|
10 |
180°00'18" |
18" |
23,6 |
0,2 |
556,96 |
0,04 |
4,72 | |
|
|
1799°59'4" |
178" |
-60 |
0 |
5258,4 |
11 55 , 6 |
-6 89 , 2 |
Вычислим r по формуле (1), которая в данной задаче примет вид:
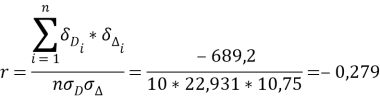
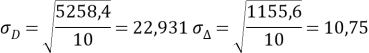
Оценка надёжности r.
Так как число измерений небольшое ( n =10), то для оценки надёжности применим критерий Фишера. Этот критерий основан на преобразовании вида
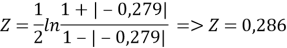
Величина Z* подчинена нормальному закону распределения. По таблице значений функции Лапласа, пользуясь коэффициентом корреляции r*, как аргументом, находим Z*=0,279. Доверительный интервал для истинного значения Z имеет вид
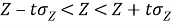
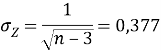
Для вероятности 0,90 по таблице интеграла вероятностей находим коэффициент t=1,645 и определяем границы доверительного интервала для Z :
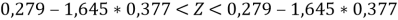
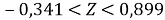
Затем из таблицы находим соответствующие крайним значениям Z(-0,341; 0,899) значения границ коэффициента корреляции (-0,33 и 0,713). Получаем доверительный интервал, с вероятностью 0,90 накрывающий истинное значение коэффициента корреляции r
—0,33
Составим уравнение регрессии Δ на D:
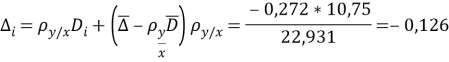
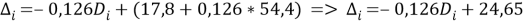
Затем по уравнению строим график. Достоинство уравнения регрессии состоит в том, что оно позволит по заданным значениям переменной D предвычислять ожидаемые в среднем значения переменной Δ.
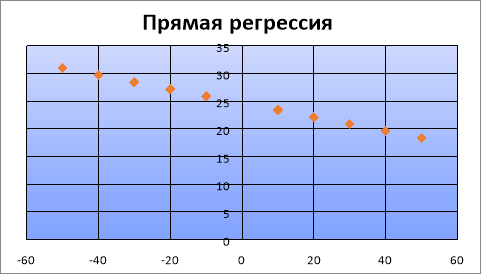
Заключение:
Величина коэффициента корреляции определяет устойчивость связи между случайными величинами, чем ближе значение к единице, тем теснее статистическая связь. В нашей задаче коэффициент вышел отрицательный, и ближе к нулю. Это свидетельствует об отсутствии прямолинейной статистической связи. Прямая регрессия будет идти на убывание это свидетельствует об отсутствии линейной связи между явлениями. Значит невязки вышли очень грубыми, это может быть систематическими ошибками или случайными ошибками при измерении. От сюда может возникнуть необходимость измерить триангуляцию с начала.
Литература:
- Гудков В. М., Хлебников А. В. Математическая обработка маркшейдерско-геодезических измерений.-М.: Недра, 1990
- Рыжков П. А., Гудков В. М. Применение математической статистики при разведке недр.-М.: Недра, 1966.
- Русяева Е. А. Теория математической обработки геодезических измерений: учебное пособие Часть I. Теория ошибок измерений. — M.: МИИГАиК, 2016.