Предварительная обработка данных является первым и неотъемлемым этапом машинного обучения, поскольку качество данных и полезная информация, которая может быть получена из них, напрямую влияют на способность нашей модели к обучению, поэтому чрезвычайно важно, чтобы мы предварительно обработали наши данные, прежде чем вводить их в нашу модель. Процесс подготовки данных может отнимать большую часть времени специалиста по работе с данными. Процесс предобработки более-менее стандартизирован, то есть предобработка данных в финансовой компании по своим этапам схожа с предобработкой данных в телекоммуникационной компании или любой другой, единственное различие в самих данных. Без предварительной обработки данных банковский специалист не сможет построить модель.
Основные задачи на этапе предобработки данных:
– Обработка нулевых значений;
– Нормализация данных;
– Борьба с выбросами;
– Обработка категориальных признаков;
– Проблема мультиколлинеарности.
Обработка нулевых значений .
1) Самый простой способ решить проблему с пропущенными значениями в выборке — игнорировать объекты, в которых есть пропуски. Этот метод применим только тогда, когда небольшая часть данных в выборке имеет пропущенные значения. Преимущество такого подхода — простота и невозможность повредить данные, заменив пробелы. Если размер выборки достаточно велик, метод может работать хорошо. Альтернативный вариант в случае пробелов в ограниченном количестве характеристик — удалить эти характеристики из выборки.
2) Другой более простой метод — заменить пропуски специальным предопределенным значением, например 0 или -9999. Такой подход позволяет не уменьшать размер выборки, но может вводить значения, сильно отличающиеся от реальных.
3) Еще один простой способ восстановить пропущенные данные — заменить их на моду или среднее значением в разрезе определенной характеристики. В случае категориального типа данных все пропуски заменяются наиболее часто встречающимся значением, в случае количественной типа данных — средним значением признака. Этот метод, в отличие от двух предыдущих, учитывает имеющиеся данные и их статистические значения. Преимущество подхода — простота, однако на практике возникает проблема с определением, является ли конкретная характеристика категориальной или количественной, особенно с большим их количеством.
4) Исходя из предположения, что близкие объекты по значениям среди заполненных признаков близки по признакам, значение которых может быть пропущено (гипотеза компактности), для восстановления пропусков в данных применяется метод k ближайших соседей (kNN). Реализация аналогична использованию классического метода k ближайших соседей, за исключением того, что для каждого объекта прогнозируется сразу несколько недостающих значений.
5) Замена с помощью метода k средних (k-Means). Подобно методу k-ближайшего соседа, предполагается, что объекты, близкие по некоторым признакам, должны быть близки и по другим признакам. Однако, в отличие от метода kNN, он ищет не ближайших соседей для каждого объекта с пропущенными значениями, а скорее информацию о центре кластера, в который попал определенный объект с промежутками.
6) Также можно заменить отсутствующие значения в определенном признаке датасета, прогнозируя его исходя из других признаков датасета, используя один из алгоритмов машинного обучения. Поскольку в признаках, используемых для обучения, отсутствуют значения, необходимо изначально заменить их одним из простейших методов восстановления пропусков. В этом случае инициализация пропущенных значений выполняется путем замены среднего значения по признаку, в качестве алгоритма прогнозирования пропущенных значений можно использовать случайный лес или линейную регрессию. Для каждого признака, у которого отсутствует значение, обучение выполняется на объектах, у которых нет пропусков в этом датасете; для остальных признаков значения этого пропущенного признака подставляются с использованием обученного алгоритма ML. Эта процедура повторяется несколько раз до сходимости или указанного максимального количества итераций в случае случайного леса, либо до достижения необходимых метрик качества в случае линейных алгоритмов.
Выбор метода заполнения пропусков может зависеть от типов данных, в которых они есть, количества объектов с пропущенными значениями и причины их наличия. Каждое действие требует индивидуального выбора метода обработки пропущенных значений
Нормализация данных. Нормализация — это преобразование данных к неким безразмерным единицам. Иногда — в рамках заданного диапазона, например, [0..1] или [-1..1]. Иногда — с какими-то заданным свойством, как, например, стандартным отклонением равным 1.
Предположим, что в наших данных о клиентах банка и их активности есть столбцы: Age и Commission. Допустим, возможен возраст от 0 до 100 лет, а комиссия — от 100 долларов до 1000. Значения и их разбросы в столбце Commission больше, поэтому алгоритм автоматически решит, что этот признак важнее возраста. А это не так: все признаки значимы. Чтобы избежать этой ловушки, признаки масштабируются — приводятся к одному масштабу.
Аналитически любая нормализация сводится к формуле
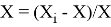
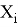
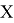
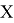
Основная цель нормализации — привести различные данные в самых разных единицах и диапазонах значений в единую форму, которая позволит нам сравнивать их друг с другом или использовать их для вычисления сходства между объектами. На практике это необходимо, например, для кластеризации и в определенных алгоритмах машинного обучения. Один из методов масштабирования — стандартизации данных. Стандартизация — это метод преобразования значений признаков, который адаптирует данные с разными диапазонами значений к работе с моделями машинного обучения, которые используют расстояние для прогнозирования. Этот вид нормализации с использованием стандартизированной оценки преобразует значения таким образом, что среднее значение вычитается из каждого наблюдения каждой характеристики, а результат делится на стандартное отклонение этой характеристики.
Такое преобразование необходимо, поскольку признаки датасета могут иметь большие различия между своими диапазонами, и для моделей Машинного обучения, основанных на вычислении дистанции между точками на графике как основу прогнозирования: Метод k-ближайших соседей (kNN), Метод опорных векторов (SVM), Дерево решений (Decision Tree) и проч., это спровоцирует искаженное восприятие данных.
Нормализация полезна, когда мы знаем, что распределение данных не соответствует гауссову, то есть нормальному. Это может пригодиться в алгоритмах, которые не предполагают никакого распределения. Стандартизация полезна в случаях, когда данные следуют гауссовскому распределению. В отличие от нормализации, стандартизация не имеет ограничивающего диапазона. Даже если в данных присутствуют выбросы, стандартизация не повлияет на них. Однако выбор между типами преобразований будет зависеть от бизнес-задачи и выбранного алгоритма ML. Не существует жесткого правила, которое подскажет, когда нормализовать или стандартизировать данные. Для выбора наилучшего решения можно использовать оба метода и сравнить их результаты на определенных заранее метриках.
Обработка выбросов. Данные могут содержать выбросы. Обычно это не ошибки, но аномально выбивающиеся значения могут исказить работу модели. Чтобы определить, является ли значение выбросом, используется выборочная характеристика, называемая межквартильным размахом. Она определяется следующим образом:
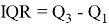
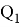
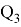
Для того, чтобы понять, является ли значение выбросом, можно воспользоваться эвристикой: выбросы лежат за пределами следующего интервала:
Чтобы понять, является ли значение выбросом, принято использовать следующую эвристику — как правило, выбросы лежат за пределами следующего диапазона:
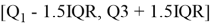
Также на практике часто принимают за выбросы значения, лежащие за пределами 2.5 % и 97.5 % квартилей. Как правило от выбросов избавляются.
Обработка категориальных признаков. Обработка категориальных переменных — еще один неотъемлемый аспект машинного обучения. Категориальные переменные — это в основном переменные, которые являются дискретными, а не непрерывными. Внешний цвет товара является дискретной переменной, в то время как его цена является непрерывной переменной.
Категориальные переменные далее делятся на 2 типа:
– Порядковые категориальные переменные — эти переменные могут быть упорядочены, например, размер футболки. Мы можем сказать, что размер M <l<xl. <="" p=""> </l<xl.>
– Номинальные категориальные переменные — эти переменные не могут быть упорядочены, например, цвет футболки. Мы не можем сказать, что синий < зеленый, так как нет никакого смысла сравнивать цвета, поскольку они не имеют никакого отношения.
Стоит отметить, что нам нужно по-разному обрабатывать порядковые и номинальные категориальные переменные.
Есть простейший кодировщий LabelEncoder для целевых значений и OrdinalEncoder для значений переменных, которые каждой категории сопоставляет некоторое целое число (собственно, номер категории).
Для кодировки порядковых переменных существует простой тип кодировка sklearn.preprocessing.LabelEncoder, которая связывает каждую категорию с целым числом (фактически, с номером категории). Аналогично можно использовать функцию map().
Самая большая ошибка, которую совершает большинство людей, заключается в том, что они не различают порядковые и номинальные переменные. Поэтому, если вы используете ту же функцию map() или LabelEncoder с номинальными переменными, модель будет думать, что между номинальными значениями существует какая-то связь, например, в нашей таблице есть 3 города: Москва, Санкт-Петербург, Киев, закодируем города через LabelEncoder(), допустим новые значения: 1, 2, 3 соответственно. В этом случае данный метод сильно упрощает данные, фактически проецируя категориальный признак на вещественную прямую. Весь смысл категориальности теряется. Более того, появляются ложные интерпретации, исходя из кодировки Москва + Санкт-Петербург = Киев, но это не характеризует наши данные, а скорее отображает особенности выбранной нами кодировки, что может запутать в последствии модель. Существует метод, который способен решить эту проблему one-hot-encoding.
Таким образом, в one-hot-encoding мы, по сути, создаем n столбцов, где n — количество уникальных значений, которые может принимать номинальная переменная. В нашем примере с тремя городами мы создадим 3 новых столбца с названиями городов, таким образом, что из 3 столбцов только один столбец может иметь значение = 1, а все остальные будут иметь значение = 0.
Резюмируем. Техникой OHE категориальные признаки переводятся в численные в два этапа:
– Для каждого значения признака создаётся новый столбец;
– Если объекту категория подходит, присваивается 1, если нет — 0.
Новые признаки называются дамми-переменными, или дамми-признаками (англ. dummy variable, «фиктивная переменная»). Для прямого кодирования в библиотеке pandas есть функция pd.get_dummies().
С прямым кодированием не всё так просто. Когда данных в избытке, можно угодить в дамми-ловушку. В таблицу добавились три новых столбца. Поскольку они сильно связаны между собой, один удалим без сожаления. Восстановить столбец можно по оставшимся двум. Так мы не попадём в дамми-ловушку.
OHE кодирование — довольно удобный способ кодирования, но с ним связана еще одна проблема, и это мультиколлинеарность. Мультиколлинеарность действительно немного сложная, но чрезвычайно важная концепция статистики.
Мультиколлинеарность — это наличие высокой взаимной корреляции между двумя или более независимыми переменными в модели. Мультиколлинеарность может привести к смещенным или вводящим в заблуждение результатам, когда исследователь или аналитик пытается определить, насколько эффективно каждая независимая переменная может использоваться для прогнозирования значения целевой переменной в статистической модели.
Как мы можем определить мультиколлинеарность:
– Использовать оценку VIF (Variance Inflation Factor) в регрессионной модели, чтобы определить, присутствует ли мультиколлинеарность в наборе данных.
– Если стандартные ошибки слишком высоки, это может быть показателем того, что одна ошибка многократно распространяется из-за перекрытия информации.
– Большие изменения параметров при добавлении или удалении новых функций указывают на сильно дублирующуюся информацию.
– Анализ корреляционной матрицы. Объекты со значениями, стабильно превышающими 0.6, являются индикаторами мультиколлинеарности.
Существует множество решений проблемы мультиколлинеарности:
– Использование алгоритмов, невосприимчивых к мультиколлинеарности, если это неотъемлемый аспект данных, а другие преобразования невозможны. Ridge regression, principal component regression или partial least squares regression — все это хорошие альтернативы классической регрессии.
– Использование PCA для уменьшения размерности набора данных и сохранения только тех переменных, которые важны для сохранения структуры данных. Это полезно, если набор данных в целом очень мультиколлинеарен.
– Удаление сильно коррелированных объектов.
– Получение дополнительных данных — это предпочтительный метод. Большее количество данных может позволить модели сохранить текущий объем информации, предоставляя контекст и перспективу для шума.
Мы рассмотрели основные этапы предобработки данных и их первичного анализа. Предобработка данных важнейшим этап построения модели машинного обучения, который может занимать до 80 % времени, так как от данного шага зависит корректность работы будущей модели. В случае ошибки в первичном анализе данных мы может допустить переобучение модели или утечку данных, которые могут ввести нас в заблуждение относительно корректности работы модели ML.
Литература:
- Уэс Маккини. Python и анализ данных / Маккини. —: ДМК-Пресс, 2020. — 540 c. — Текст: непосредственный.
- Introduction to Data Preprocessing in Machine Learning. — Текст: электронный // Towardsdatascience: [сайт]. — URL: https://towardsdatascience.com/introduction-to-data-preprocessing-in-machine-learning-a9fa83a5dc9d (дата обращения: 28.12.2021).
- Effective Data Preprocessing and Feature Engineering. — Текст: электронный // becominghuman.ai: [сайт]. — URL: https://becominghuman.ai/effective-data-preprocessing-and-feature-engineering-452d3a948262 (дата обращения: 28.12.2021).
- Предварительная обработка данных. — Текст: электронный // habr.com: [сайт]. — URL: https://habr.com/ru/post/511132/ (дата обращения: 28.12.2021).

