Возрастающее быстродействие современных вычислительных систем требует увеличения скорости передачи данных. В силу различных помех прием двоичных данных может быть ошибочным. В результате возникает проблема обеспечения надежной передачи цифровой информации по каналам с шумами. Важнейший вклад в решение данной проблемы вносит теория помехоустойчивого кодирования.
Известно, что главное преимущество программной реализации кодов — это низкая стоимость и простота реализации. Но при этом у нее есть такие недостатки как низкая производительность, загрузка дополнительной работой центрального процессора.
Аппаратные реализации стоят дороже, чем программные, так как используют дополнительную аппаратуру для выполнения операций. При этом они разгружают центральный процессор и системную шину и позволяют увеличить быстродействие, за счет замены последовательностей операций на операцию, выполняемую за один такт. Большей аппаратной производительности можно достичь путем применения компонентной базы — программируемых логических интегральных схем (ПЛИС). Таким образом, применение ПЛИС дает большую аппаратную гибкость за счет его реконфигурируемости, а также возможность отладки и, при необходимости, изготовки в кремнии без избыточности, присущей ПЛИС.
Для исследования были выбраны коды по следующим критериям. Код для проверки целостности данных — CRC (Cyclicredundancycheck) код, базирующийся на полиномиальной арифметике, код, который предназначен для исправления однократной ошибки — код Хэмминга (простейший линейный код) и код для исправления многократных ошибок — Код Рида-Соломона (недвоичный линейный код) [1].
Языком описания был выбран SystemVerilog, служащий для описания и верификации аппаратуры, являющийся расширением языка Verilog. Для исследования аппаратной реализации данных алгоритмов использовалась ПЛИС типа FPGA семейства Cyclone III, разработанной фирмой Altera на 39600 логических элементов. Была выбрана среда проектирования Quartus II, соответствующая данной ПЛИС, а также инструмент логического синтеза DesignVision.
Основным достоинством аппаратной реализации помехоустойчивых кодов на FPGA является параллельное вычисление. Аппаратная реализация алгоритмов в первую очередь нужна для получения максимального быстродействия выполнения операций кодирования и декодирования в устройстве.
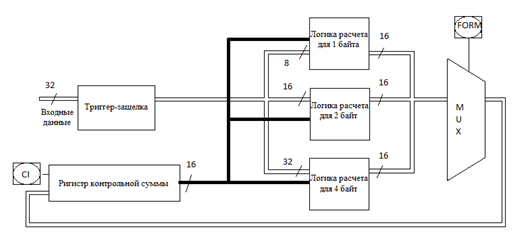
Рис. 1. Функциональная схема для блока вычисляющий CRC код для одного байт, слово и двойное слово
Блок состоит из регистра управления, регистра контрольной суммы и логики расчета CRC. С помощью регистра управления можно: включить и выключить режим начального заполнения; установить формат записываемых данных. Одним из битов регистра управления является СI — бит инициализации контрольной суммы. Мультиплексор управляется сигналом FORM — поле задания формата записываемых данных. Триггер-защелка применяется для защелкивания входных данных. Регистр контрольной суммы используется для инициализации контрольной суммы, приема данных, для которых вычисляется контрольная сумма и считывания полученного значения контрольной суммы.
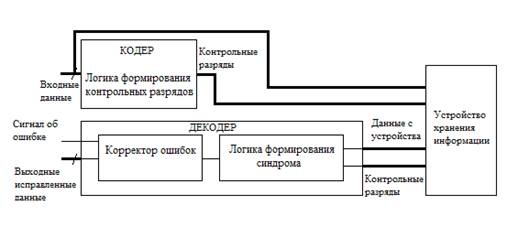
Рис. 2. Функциональная схема для блока реализующий код Хэмминга
Кодирование и декодирование кодов Рида — Соломона является довольно сложной задачей. Его решение выливается в громоздкий, запутанный и крайне неочевидный код, который требует широких знаний от разработчика во многих областях высшей математики [3].
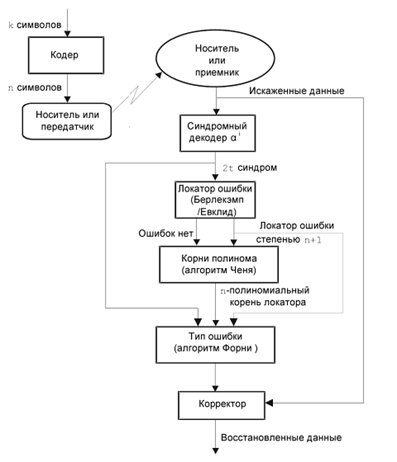
Рис. 3. Функциональная схема декодирования кода Рида — Соломона
На рисунке представлена типовая схема декодирования, которая получила название авто регрессионного спектрального метода декодирования. Существует много различных схем для декодирования данных с использованием кода Рида — Соломона. Представленная на рисунке 3 схема декодирования является универсальной. Архитектура кодера представляет собой соединение сдвиговых регистров, которые объединены с помощью сумматоров и умножителей, функционирующих по правилам арифметики Галуа [1].
Важным этапом разработки является синтез логической схемы. Логический синтез — это процесс получения списка соединений логических вентилей из абстрактной модели поведения логической схемы (например, на уровне регистровых передач (RTL — RegisterTransferLevel)) [2].
В среде проектирования Quartus II для каждого блока функциональной схемы приводится ряд следующих элементов: LogicCells (общее количество ячеек для элемента); LC Resisters (общее количество регистров в одной ячейке); LUT (OnlyLCs — количество элементов только комбинаторной логики, входящих в ячейку);Register — OnlyLCs (количество элементов только регистровой логики); LUT/RegisterLCs (количество элементов комбинаторной либо регистровой логики) [4].
Таблица 1
Результат синтеза для блока, вычисляющий код CRC для одного байта данных, слова и двойного слова.
|
Hierarchy Node |
Logic Cells |
Logic Registers |
LUT-Only LCs |
Registers-Only LCs |
LUT/Registers LCs |
|
CRC |
242 |
36 |
206 |
4 |
32 |
Таблица 2
Результат синтеза для Хэмминга
|
Hierarchy Node |
Logic Cells |
Logic Registers |
LUT-Only LCs |
LUT/Registers LCs |
|
Hamming |
147 |
2 |
145 |
2 |
|
-decod |
41 |
0 |
41 |
0 |
|
-encod |
27 |
0 |
27 |
0 |
Количество занимаемых логических ячеек для блока реализующий код Хэмминга на FPGA фирмы AlteraCyclone III, что составляет менее 1 % кристалла. Totallogicelements 147 / 39600 (< 1 %).
Результаты, полученные на этапе синтеза используя библиотеку Altera для блока реализующий код Рида — Соломона.
Таблица 3
Результат синтеза для кода Рида — Соломона.
|
Hierarchy Node |
Logic Cells |
Logic Registers |
LUT-Only LCs |
Memory Bits |
Registers-Only LCs |
LUT/Registers LCs |
|
RS_top |
1409 |
1168 |
54 |
211 |
1198 | |
|
-decod |
2342 |
1201 |
1141 |
54 |
202 |
999 |
|
-encod |
350 |
27 |
0 |
9 |
199 |
Количество занимаемых логических ячеек для блоков, реализующих код CRC и Хэмминга на FPGA фирмы AlteraCyclone III, составляет менее 1 % кристалла, что показывает их простоту реализации и малое количество затрат ресурсов при разработке. Код Рида — Соломона занимает 2692 элементов из 39600, что составляет 7 % кристалла. Такие аппаратные затраты кода Рида — Соломона объясняются его эффективностью работы.
В результате синтеза была получена оценка логических элементов, занимаемых каждым блоком в ПЛИС. Для дальнейшей разработки их “в кремнии” нужно провести синтез в библиотеке TSMC по нормам 90 нм, для получения оценки задержек, а также площади блоков на кристалле.
Очевидно, что блоки, реализующие каждый из рассмотренных алгоритмов, должны работать «в связке» с устройством обработки информации. Таким устройством было выбрано микропроцессорное ядро KM211 семейства КРОЛИК. При синтезе было установлено ограничение на временные задержки 1 нс. В результате синтеза при заданных условиях для всех блоков задержка составила не более 1нс. Это значит, что возможно использование блока, реализующего каждый из рассмотренных кодов, как отдельного функционального блока в микроконтроллере.
Площадь блока Рида-Соломона составляет 19000 мкм2, что почти в 15 раз больше площади, занимаемой блоком, реализующим код Хэмминга. Это занимает довольно большую площадь кристалла, что влияет на сумму при заказе микроконтроллера. Для примера, площадь ядра KM211 семейства КРОЛИК, занимаемая в кремнии, составляет 90000мкм2.
В работы были исследованы некоторые методы кодирования для повышения надежности хранения информации, а именно: циклический избыточный код (CRC код), код Рида — Соломона и код Хэмминга.
СRC код является удачным решением в тех случаях, когда коррекция ошибок не требуется и достаточно лишь проверить, успешно ли прошла передача [3]. Этот метод обладает такими достоинствами как невысокие затраты ресурсов, простота реализации в аппаратных устройствах, а также готовый сформированный математический аппарат из теории линейных циклических кодов. Поэтому этот код является популярным, а также хорошим средством для обнаружения ошибок на практике, например, когда возникают ошибки из-за наличия в канале передачи данных шума.
Коды Хэмминга — это наиболее известные из самоконтролирующихся и самокорректирующихся кодов [3]. Код Хэмминга способен обнаружить и исправить однократную ошибку. Существует модифицированный код Хэмминга, способный исправлять одиночную и обнаруживать двойную ошибки.
Коды CRC и Хэмминга в отличие от Рида-Соломона используют меньше аппаратных затрат, а также площади в кристалле, что позволяет в дальнейшем реализовать их в виде отдельного функционального блока для микроконтроллера КРОЛИК. Такие коды можно использовать для повышения надежности хранения ключевой информации, например, в банковских картах. При этом данное улучшение не будет сильно влиять на сложность устройства и удобство пользования картой.
Код Рида — Соломона является наиболее мощным кодом, который исправляет многократные пакеты ошибок. В настоящий момент коды Рида — Соломона имеют очень широкую область применения благодаря их способности находить и исправлять многократные пакеты ошибок. Их можно применять для исправления ошибок во многих системах: устройствах памяти, беспроводных или мобильных коммуникациях, спутниковых коммуникациях, цифровом телевидении. Тем не менее, процессы кодирования и декодирования требуют больших затрат, что сильно ограничивает область его применения.
Литература:
1. Питерсон У. Коды, исправляющие ошибки // М.: Мир, 2009. — 593 c.
2. Максфилд К. Проектирование на ПЛИС. Курс молодого бойца // М.: Издательский дом «Додэка-XXI», 2007. — 408 с.
3. Бояринов И. М. Самопроверяющиеся схемы и алгоритмы декодирования двоичных кодов Хэмминга, БЧХ-кодов и кодов Рида-Соломона // М.: Институт системного анализа РАН, 2008. — 111 с.
4. Поляков А. К. Языки VHDL и Verilog в проектировании цифровой аппаратуры на ПЛИС // М.: МЭИ, 2012. — 221 с.

