В статье автор раскрывает роль заданий историко-математического содержания на уроках алгебры их использование в конкретных разделах математики.
Ключевые слова: история математики, алгебра, задания историко-математического содержания, задания с элементами историзма.
Введение новых образовательных стандартов основного общего образования в качестве актуальной проблемы современного урока определило необходимость всестороннего и гармонического развития личности каждого ученика. Это предполагает:
– освоение школьниками в ходе изучения учебного предмета умений, специфических для данной предметной области, видами деятельности по получению нового знания в рамках учебного предмета, его преобразованию и применению в учебных, учебно-проектных и социально-проектных ситуациях;
– формирование научного типа мышления; формирование готовности и способности, обучающихся к саморазвитию и личностному самоопределению;
– формирование их мотивации к обучению и целенаправленной познавательной деятельности;
– формирование системы ценностно-смысловых установок [5].
В этих условиях необходимо в каждом учебном предмете найти методические возможности для эффективного решения вышеназванной проблемы.
В последнее время как в средней, так и в профильной школе ведется активный поиск инновационных форм, методов и содержания школьного образования, которые могли бы создавать условия для роста интеллектуальных способностей учащихся.
Одним из возможных путей решения этой проблемы может быть названо использование историко-математического материала в процессе обучения алгебре учащихся профильной школы. Именно трактовка «интеграция историко-математического материала с учебным» позволяет реализовать весь методический потенциал исторического подхода в обучении математике, особенно в профильной школе. Понятие «интеграция» трактуется как восстановление, объединение в целое каких-либо частей, элементов; как состояние связанности в целое отдельных дифференцированных частей, а также как процесс, ведущий к такому состоянию. В обучении интеграцию часто понимают как взаимовлияние, взаимопроникновение и взаимосвязь содержания различных учебных дисциплин. Интеграция историко-математического материала с учебным может осуществляться как на уровне теоретического материала, так и на уровне задач [2].
Рассмотрим применение данных задач в разделе математики «Комбинаторика».
Комбинаторика (комбинаторный анализ) — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них.
Содержательная линия проходит через весь курс математики. В 5–6 классах рассматривается существование и построение комбинаций с заданными свойствами, перебор всех возможных вариантов. В 7–9 классах речь идет о комбинаторных правилах произведения и сложения. В 10–11 классах рассматриваются размещения, перестановки сочетания, формула бинома Ньютона.
Главным средством для развития у школьников сильной заинтересованности к предмету математики, к ее истории — это постановка перед учащимися проблемных задач, а именно, заданий историко-математического содержания. Эти задания реализуют следующие функции: образовательные, воспитательные и развивающие.
Продемонстрируем включение задач историко-математического содержания в изучении темы «Комбинаторика» в 11 классе. Поурочное планирование по Ю. М. Колягину выглядит примерно следующим образом: «Математическая индукция» (1 ч.); «Правила произведения. Размещения с повторениями» (1 ч.); «Перестановки» (2 ч.); «Размещение без повторений» (1 ч.); «Сочетание без повторений и Бином Ньютона» (3 ч.); «Сочетания с повторениями» (1 ч.); «Урок обобщения и систематизации знаний» (1 ч.).
Тема третьего урока главы «Комбинаторика» — «Перестановки». Цель урока: вывести формулу числа перестановок из n элементов. Для реализации образовательной функции на этапе построения проекта выхода из затруднения можно привести следующую задачу:
Задача. В знаменитой басне Крылова «Квартет» «проказница Мартышка, Осёл, Козёл да косолапый Мишка» устроили любопытный эксперимент: они исследовали влияние взаимного расположения музыкантов на качество исполнения. И если бы не вмешался Соловей, участники квартета, наверное, перепробовали бы все возможные варианты. Зададимся вопросом: сколько существует способов, чтобы рассадить в один ряд, четырёх музыкантов [1]?
При решении данной задачи учащиеся говорят о том, что на первое место можно поставить любое из четырех животных, на второе — любое из трех оставшихся, на третье — любое из двух оставшихся и на четвертое — последнее оставшееся животное. Затем, применяя уже известное правило произведения, получаем
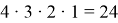
т. е. животных можно расположить 24 способами.
С помощью данной задачи учащихся можно не только подвести к определению понятия «перестановки из n элементов», но и к формуле числа перестановок из n элементов, которую будут применять при решении других задач этой темы.
На втором уроке по теме «Перестановки» для реализации образовательной и развивающей функции учащимся можно предложить задачу историко-математического содержания, направленную на формирование познавательного интереса и интереса к изучению предмета, например, известную анаграмму Христиана Гюйгенса.
Задача. Когда Х. Гюйгенс (1629–1695) открыл кольцо Сатурна, он составил следующую анаграмму [6]:
aaaaaaa ccccc d eeeee g h iiiiiii llll mm
nnnnnnnnn oooo pp q rr s ttttt uuuuu
Этими буквами записывается фраза «Annulo cingitur tenui, plano, nusquam cohaerente, ad eclipticam inclinator» («Окружен кольцом тонким, плоским, нигде не подвешенным, наклонным к эклептике»). Сколько различных анаграмм можно составить из букв зашифрованной Гюйгенсом фразы.
На уроке по теме «Размещение без повторений», для реализации развивающей функции, учащимся можно предложить свою задачу, которая будет содержать какой-то исторический факт.
Также, для реализации развивающей функции, на втором уроке «Сочетание без повторений и Бином Ньютона» учащимся можно предложить выполнить мини-исследование по использованию Бинома Ньютона.
На уроке обобщения и систематизации знаний можно рассмотреть с учащимися «Задачу о восьми ферзях», для реализации воспитательной функции.
1 июня 1850 г. в «Иллюстрированной газете» под рубрикой «Шахматы» была напечатана следующая задача: «Расставить восемь ферзей на шашечнице так, чтобы ни один ферзь не угрожал другому» [3].
Эта задача еще не решена, но все же какие-то результаты получены. Можно разобрать с учащимися решение известного математика Гаусса.
В заключение статьи отметим, что на большинстве уроков алгебры задания с элементами историзма могут выполнять те функции, которые выполняет учебный материал. Эффективное включение таких заданий в содержание уроков будет способствовать и формированию познавательных интересов учащихся, и более глубокому пониманию изучаемого материала, и расширению кругозора учащихся, и решению других многочисленных задач, возникающих в практике обучения.
Литература:
- Баврин, И. И. Старинные задачи: книга для учащихся / И. И. Баврин, Е. А. Фрибус. — М.: Просвещение, 1994. — 128 с.
- Безенкова, Е. В. Использование исторического компонента на уроках математики / Е. В. Безенкова // Санкт-Петербургский образовательный вестник. — 2017. — № 6 — С. 10–13.
- Попов, Г. Н. Сборник исторических задач по элементарной математике / Г. Н. Попов. — М.: Комкнига, 2013. — 216 с.
- Саранцев Г. И. Методика обучения математике в средней школе: учеб. пособие для студентов мат. спец. пед. вузов и ун-тов. — М.: Просвещение, 2002.
- Федеральный государственный образовательный стандарт основного общего образования (утвержден приказом Министерства образования и науки Российской Федерации от 17 декабря 2010 г. № 1897) [Электронный ресурс]. — URL: http://www.edu.ru/db/mo/Data/d_10/m1897.html (дата обращения:14.12.2021).
- Чистяков, В. Д. Старинные задачи по элементарной математике / В. Д. Чистяков. — Минск: Вышэйш. школа, 1978. — 272 с.

