Данная научная статья направлена на рассмотрение проблемы формирования у обучающихся исследовательских умений при решении нестандартных задач по математике в основной школе. Целью работы является раскрытие дидактических условий организации творческой личности в процессе использования нестандартных задач на уроках алгебры. В работе приводится анализ текстовых задач многих современных методистов и психологов. Полученные результаты будут интересны педагогическим работникам школ, с целью рационального планирование уроков математики в основной школе.
Ключевые слова: исследовательские умения, нестандартные задачи, творческая активность, мотивационный компонент.
Научная статья посвящена проблемам поиска средств развития мыслительных способностей, связанных с творческой деятельностью учащихся, как в коллективной, так и в индивидуальной форме обучения. Большинство специалистов, деятельность которых направлена на модернизацию задачного материала школьной математики, представленной в современных учебных пособиях, как правило, представляют алгоритмический способ решения задач, таким образом, трудности, которые могли бы возникнуть при решении таких заданий, сводятся только к техническому характеру, для устранения которых нужно тренироваться в решении однотипных задач.
В настоящее время существует огромное количество подходов к определению «нестандартные задачи», из которых можно вынести следующий итог: чтобы соблюсти те условия, которые необходимы нам для организации систематической работы по формированию и развитию у учащихся творческого нестандартного мышления, нам необходимо проводить урок, насыщенный элементами творческих заданий, хотя бы в виде дополнительных карточек.
При решении нестандартных задач у обучающихся формируются такие умения, как наблюдение, анализирование, сравнение тех или иных объектов, обобщение фактов, а также способность делать выводы; их рассуждение становится более сформированным, доказательным, логичным, а речь аргументированной, четкой, сформированной. Решение данных задач расширяет кругозор ученика в математике, формирует у него нестандартность мышления, а также умение применять знания в творческих или нестандартных ситуациях, помогает развить упорство в достижении поставленных им целей и привить интерес к познанию в математике.
На основе методических исследований, а также на практике можно увидеть, что, столкнувшись с нестандартной задачей, обучающийся начинается теряться, впоследствии и вовсе отказываются от решения данных задач. Такое поведение связано с тем, что ученики недостаточно используют свои умения, стратегии действий при решении различных задач, а именно не могут самостоятельно составить некоторый план действий и соотнести его с полученными результатами.
Методологи считают, что любая задача в различных условиях может быть как нестандартной, так и типовой. Так, например, обычная задача экспериментального курса А. И. Маркушевича, А. М. Пышкало, «на аэродроме было 5 самолетов и 7 вертолетов, 6 машин поднялись в воздух. Можно ли утверждать, что в воздухе находится хотя бы один самолёт; хотя бы один вертолет?» Данная задача является нестандартной для действующего курса по математике первых — четвертых классов. Но в 6 классе такие задачи являются типовыми, то есть, нестандартная задача становится типовой, как только программа требует обязательного усвоения алгоритма для решения подобных задач всеми учащимися.
Изучая наблюдение методологов, мы видим, что около 40 % учителей и преподавателей школьного уровня не придают значения нестандартным задачам и не используют их на практике, либо неверно толкуют понятие «нестандартная задача». Анализ работы педагогов некоторых школ и разработой учителей, а также интернет-источник показали, что около 11 % преподавателей близки к пониманию значения нестандартных задач.
Под нестандартными задачами обычно подразумевают задачу, для решения которой нет (и не существует) образца. Систематическое решение задач данного типа способствует развитию умственной деятельности учащихся, а также формированию математических представлений. Но как же реализовать интерес у обучающихся к решению нестандартных задач? Убеждение или уговоры не всегда могут активизировать мысли ученика. Для того, чтобы привлечь школьников к решению таких задач, а следственно, к умственному труду, необходимо заинтересовать ребенка. Для того, чтобы привлечь внимание учеников или вызвать их удивление, учителя используют различного вида педагогические технологии, а также поощрение для того, чтобы удержать интерес к математике.
Однако многие учителя отказываются от использования нестандартных задач на уроках, объясняя это тем, что первоочередным остается подготовка к ЕГЭ и ОГЭ, а для нестандартных задач просто не хватает времени.
Естественно, больше всего сложностей при решении у учащихся вызывают нестандартные задачи, которые занимают главное место среди задач повышенной трудности, но в отличие от нестандартных задач, в них есть алгоритм решения. Как говорилось ранее, одна и та же задача может быть стандартной или нестандартной в зависимости от того, кто решает эту задачу (соответствует ли оно возрасту, навыкам и умениям, программе).
Например, задача: При каких натуральных значениях
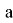
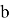
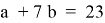
Для того, чтобы научить школьников решать нестандартные задачи, необходимо, чтобы у них было желание, для этого задачи должны быть интересными, содержательными и своего рода привлекательными с точки зрения ученика, как мы знаем, наибольший интерес у обучающихся вызывают задачи, связанные с окружающим миром, или жизнью, которые соответствующим образом связаны с вещами, которые знакомы учащимся, с их опытом, которые имеют понятную для ученика цель.
Естественно, большой ошибкой будет приучать учащихся решать только те задачи, которые у них вызывают интерес, однако такие задачи решаются учеником легче, ведь свой интерес к решению таких задач он может в дальнейшем перебросить и на скучные, не заинтересовавшие его разделы. Предложенные задачи не должны быть слишком легкими или трудными, ведь отсутствие способа решения или неспособность разобраться с задачей может привести к потере веры в себя и в свои силы.
Нельзя сказать точно, можем ли мы обучить детей решению нестандартных задач, даже если мы будем под этим понимать обучение методам поиска для решения таких задач.
Процесс решения нестандартных задач мы можем разделить на два основных элемента: 1– представление задачи, то есть описание, 2 — это непосредственно поиск решения нестандартной задачи. Главным элементом процесса решения нестандартных задач является поиск решений. В некоторых случаях поиск может способствовать нахождению всех решений или одного из решений, которые наиболее коротко и рационально представляют наше решение задачи, также может выступать установлением возможности или невозможности решения (то есть присутствием или его отсутствием).
Существует два подхода к решению нестандартных задач. Первый подход характеризует представление задачи в пространстве состояний; второй характеризуется редукцией или своду задачи к альтернативной совокупности (то есть к подзадачам). Чаще всего используют второй подход. Для использования этих подходов в обучении школьников математике просто необходима теоретическая и практическая подготовка в данных областях.
Для диагностики развития творческой активности у учащихся средствами нестандартных задач необходимо провести экспериментальную поэтапную работу, на констатирующем этапе нужно определить уровень сформированности готовности к решению задач. Для этого существует множество различных тестирований, которые мы и будем использовать. Выделяют несколько основных уровней развития творческой активности учащихся, такие как креативный, мотивационный и деятельностный компоненты творческой активности.
Для определения уровня развития мотивационного компонента будем вести подсчет степени и частоты проявления личностных свойств, таких как: умение поставить цель и достигнуть ее. Такой компонент, как деятельностный, мы будем определять по умению самостоятельно работать, а также по степени развитости качеств предмета с операционной стороны творческой деятельности (а именно исполнительности, инициативности и так далее).
Креативный механизм творчества составляется из условий устойчивости проявления выделенных качеств. Для исследования и диагностики творческой активности, а также творческой деятельности учащихся нам необходимо проследить и выделить типичные уровни творческой активности учащихся.
Мы выделили три уровня творческой активности обучающихся: высокий, средний и низкий. Используя различные показатели и критерии из психолого-педагогической литературы, мы дифференцировали основные уровни развития творческой активности учеников.
При низком уровне — отсутствует потребность пополнения знаний, умений и навыков. Средний уровень — характеризуется редким наличием потребности в пополнении знаний, умений и навыков. Высокий уровень– характеризуется постоянным стремлением удовлетворять потребности в пополнении знаний, умений и навыков, проявляется в устойчивости познавательных интересов.
Диагностирующий эксперимент проводился на базе МБОУ СОШ № 28 г. Белгорода во время внеурочных занятий. В этом исследовании приняли участие 86 обучающихся.
Из этих 86 учащихся 26 человек — ученики 5 класса, 20 человек — обучающаяся 6 класса, 23 человека — ученики 7 класса и 18 человек — учащиеся 8 класса. Основная задача проводимого диагностирующего эксперимента заключалась в выявлении уровня творческой активности обучающихся.
В приведённом нами исследовании, для изучения уровня развития креативности как компонента творческой активности учащихся были применены следующие психодиагностические методики: образные тесты творческого мышления Торренса, а также некоторое количество тестов креативности Туник. Под креативностью мы должны понимать способность порождать необычные идеи, быстро разрешать проблемные ситуации, отклоняться от традиционных схем в мышлении. Понятие «креативность» охватывает некоторую совокупность личностных качеств и мыслительных, необходимых для становления способности к творчеству.
Результаты входной диагностики творческой активности обучающихся показали нам следующие данные эксперимента рис. 1:
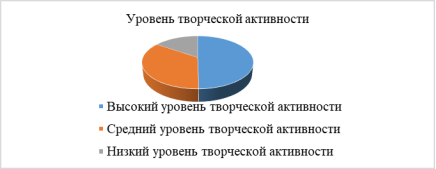
Рис. 1. Уровень творческой активности обучающихся
– Высокий уровень творческой активности — 49,6 %
– Средний уровень творческой активности — 34,7 %
– Низкий уровень творческой активности — 15,4 %
Данные диагностики экспериментальные исследования проводились для определения критериев и показателей творческой активности обучающихся, на основании чего нам удалось выявить уровень творческой активности испытуемых. Эти уровни необходимы для дальнейшего исследования по развитию творческой активности обучающихся с помощью нестандартных задач по математике.
На основе данных методических рекомендаций можно разработать кружок по решению нестандартных задач для учащихся основной школы, таким образом, решение нестандартных задач способствует активному развитию нестандартного мышления у учащихся, что становится хорошей основой для дальнейшего обучения в старших классах, а также в будущей трудовой деятельности. В повседневной жизни большинство задач, требующих решения, именно нестандартные, и решить их обычными способами не получается. В процессе развития математических способностей происходит активное интеллектуальное развитие учащихся, формируются основные структуры мышления. Математические способности особенно эффективно развиваются в процессе решения нестандартных задач.
Литература:
1. Акимова А. С. Занимательная математика. — Санкт-Петербург: Тригон, 1997. — 608 С.
2. Галкин Е. В. Нестандартные задачи по математике: Задачи логического характера / Е. В. Галкин, — М.: Просвещение; Учебная литература, 1996. — 160 С.
3. Ковалевская О. Н.,Васильева И. П., Мурова О. И.:Программа прикладного курса «Нестандартные задачи по математике» для 5–6 классов, Курск 2010–2011. -64 С.
4. Сухин И. Г. 800 новых логических и математических головоломок. — М.: АСТ, 2008. — 270 С.
5. Шкильменская Н. А. Зачем решать задачу различными способами? // Начальная школа. — 2010. — № 05. — С. 47–50

