Исходные данные
Предположим, что задано некоторое конечное множество вершин в трёхмерном Евклидовом пространстве и множество не упорядоченных пар из этих вершин, или рёбер:
|E |= n , |V |= m , (n,m) = 1,2,3, . . . (1)
Таким образом задан не ориентированный симметричный граф G(V,E ). На заданном графе требуется построить минимальный элементарный цикл или цикл Гамильтона.
Метод построения
Для решения задачи построения заданного цикла будем применять так называемый Алгоритм выбора selection Algorithm, который в свою очередь будет состоять из некоторой последовательности функций выбора selection Function, по максимально удалённой паре вершин заданного графа или по диаметру графа diam(G ) :
Alg(diam(G )) = { F(V, E ) } (2)
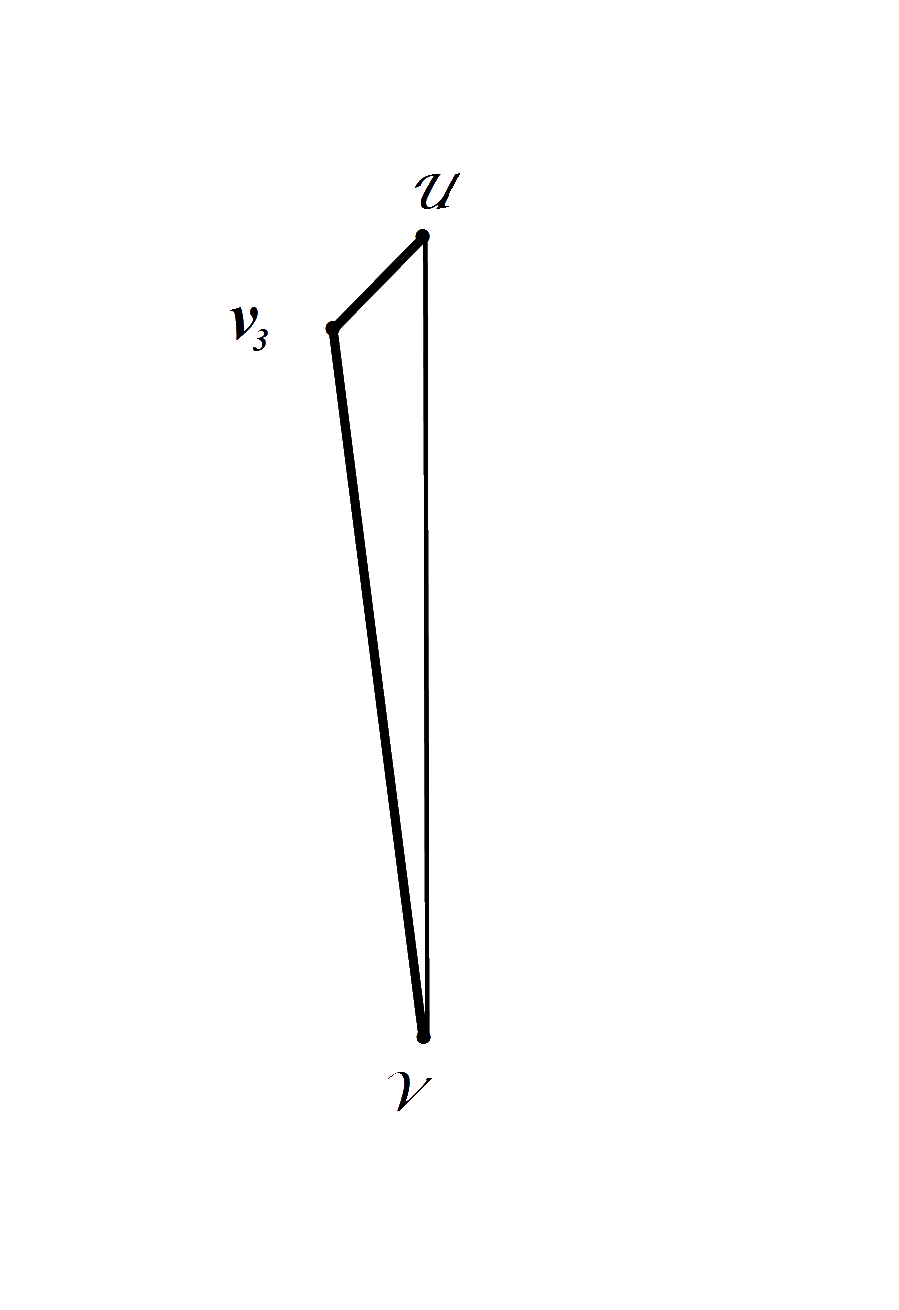
Совместим первый и второй этапы построения в связи с их простотой. Для этого выберем пару вершин из |V | = m, максимально удалённых друг от друга, которые будут определять максимальное ребро заданного графа или его диаметр:
Emax = En = diam(G ) (3)
(V1,V2) inclued {V } (4)
Затем выберем следующую вершину V3 , которая находится на максимальном расстоянии от одной из вершин диаметра графа или от одного из так называемых полюсов графа
pol(G ) = { V, U } (5)
En = {V, U } (6)
Каждую последующую вершину будем определять так же, как вершину которая в свою очередь максимально удалена от одной из вершин диаметра графа diam(G ). Соединим вершины ребра En = diam(G ) с вершиной V3 по кратчайшему пути, соответственно.
Для наглядности процесса построения предположим, что множество всех вершин |V | расположено внутри некоторой мнимой сферы. И такая сфера сжимается равномерно по всем направлениям. Тогда поверхность этой сферы будет последовательно касаться всех вершин, начиная от самых удалённых друг от друга и заканчивая менее удалёнными соответственно, до тех пор пока поверхность этой сферы соединит или коснётся всех вершин из |V | по очереди в порядке уменьшения расстояния между ними.
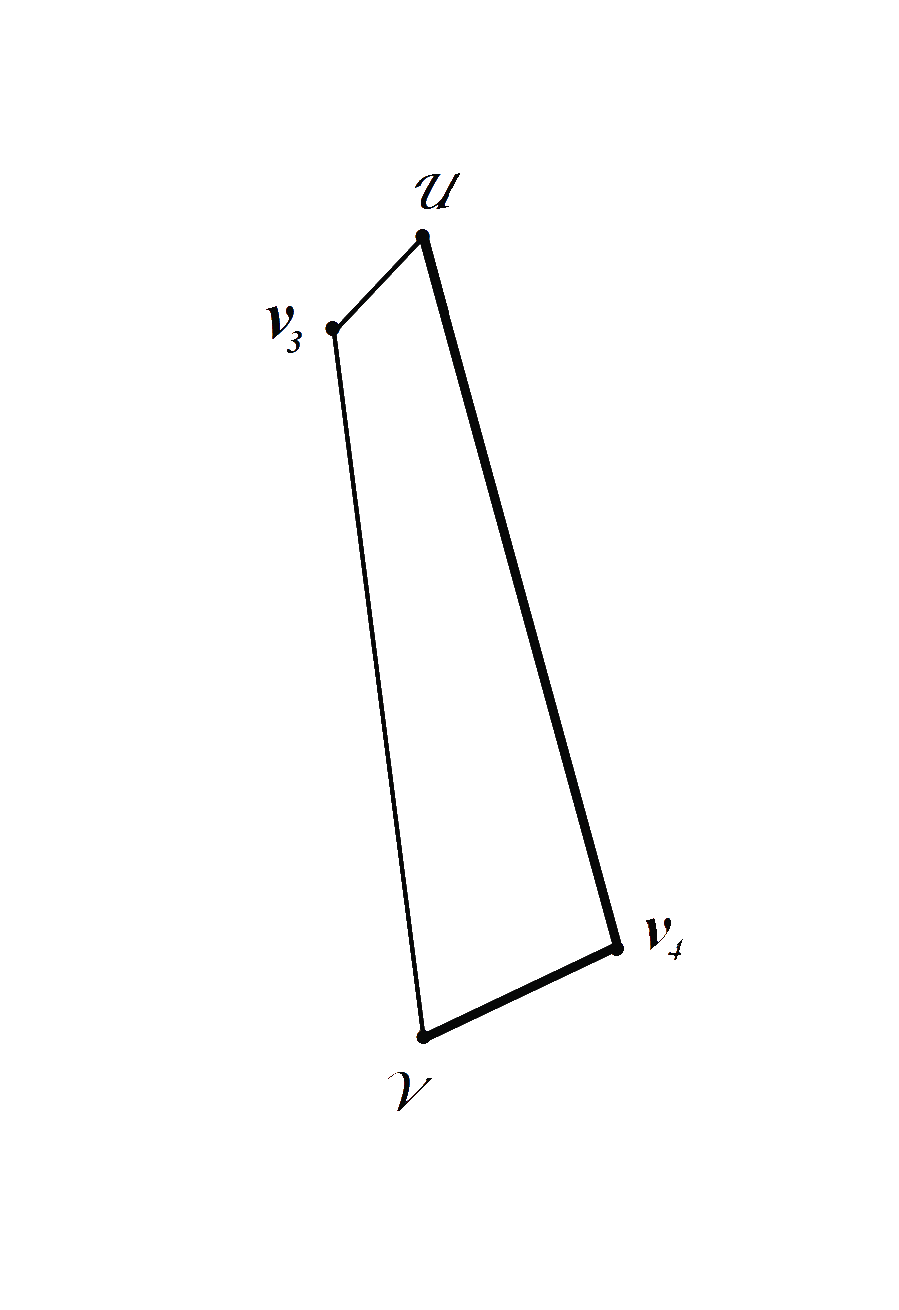
Далее выберем следующую новую вершину V4 , которая в свою очередь будет так же максимально удалена от одного из полюсов графа. Соединим вершину V4 с вершинами ближайшего к ней ребра из предыдущего цикла. Одна из вершин такого ближайшего ребра будет находиться на минимальном расстоянии от новой вершины V4 , а другая вершина такого ребра будет находиться на максимальном расстоянии от той вершины диаметра графа, которая является ближайшей к этой же новой вершине V4.
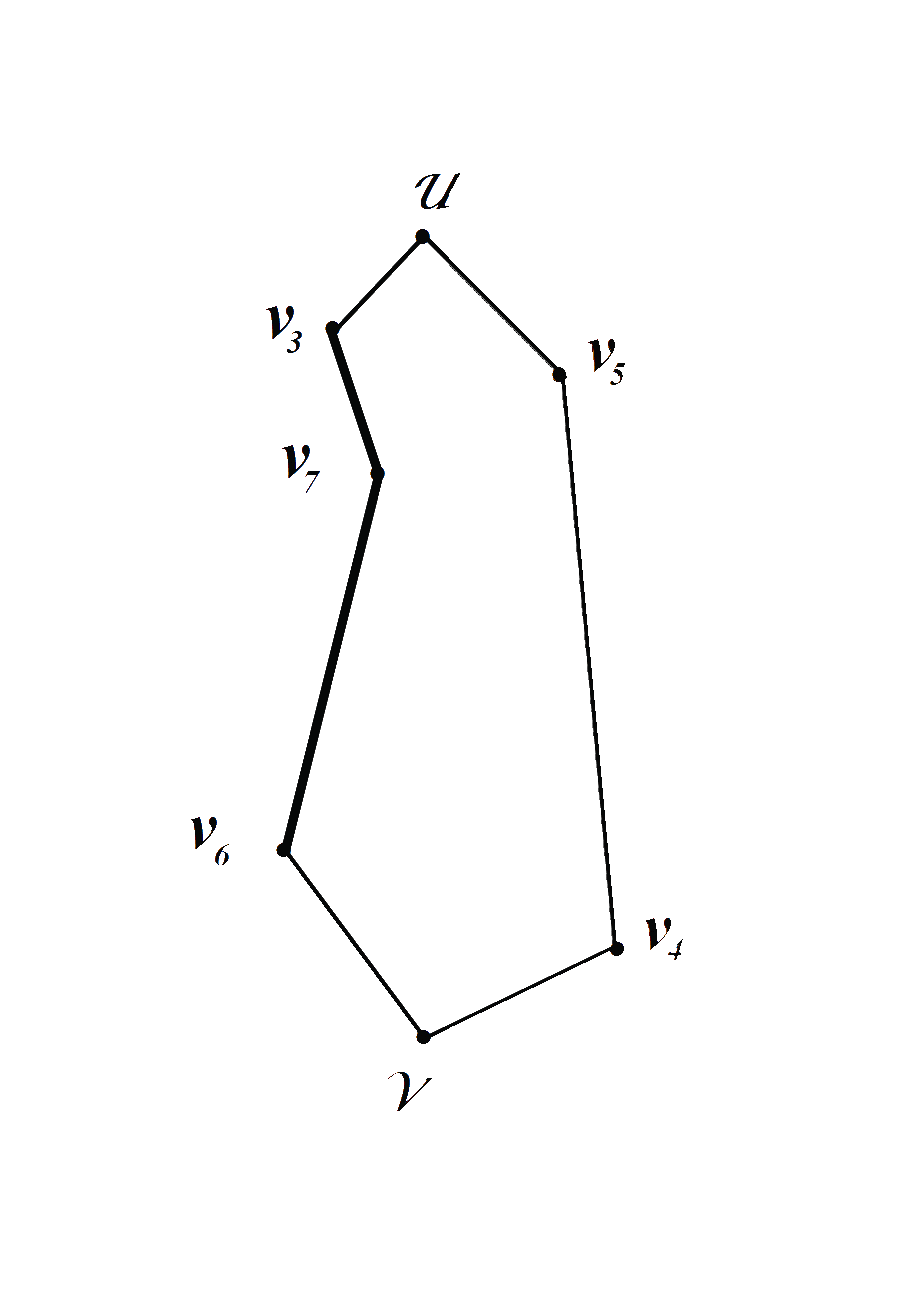
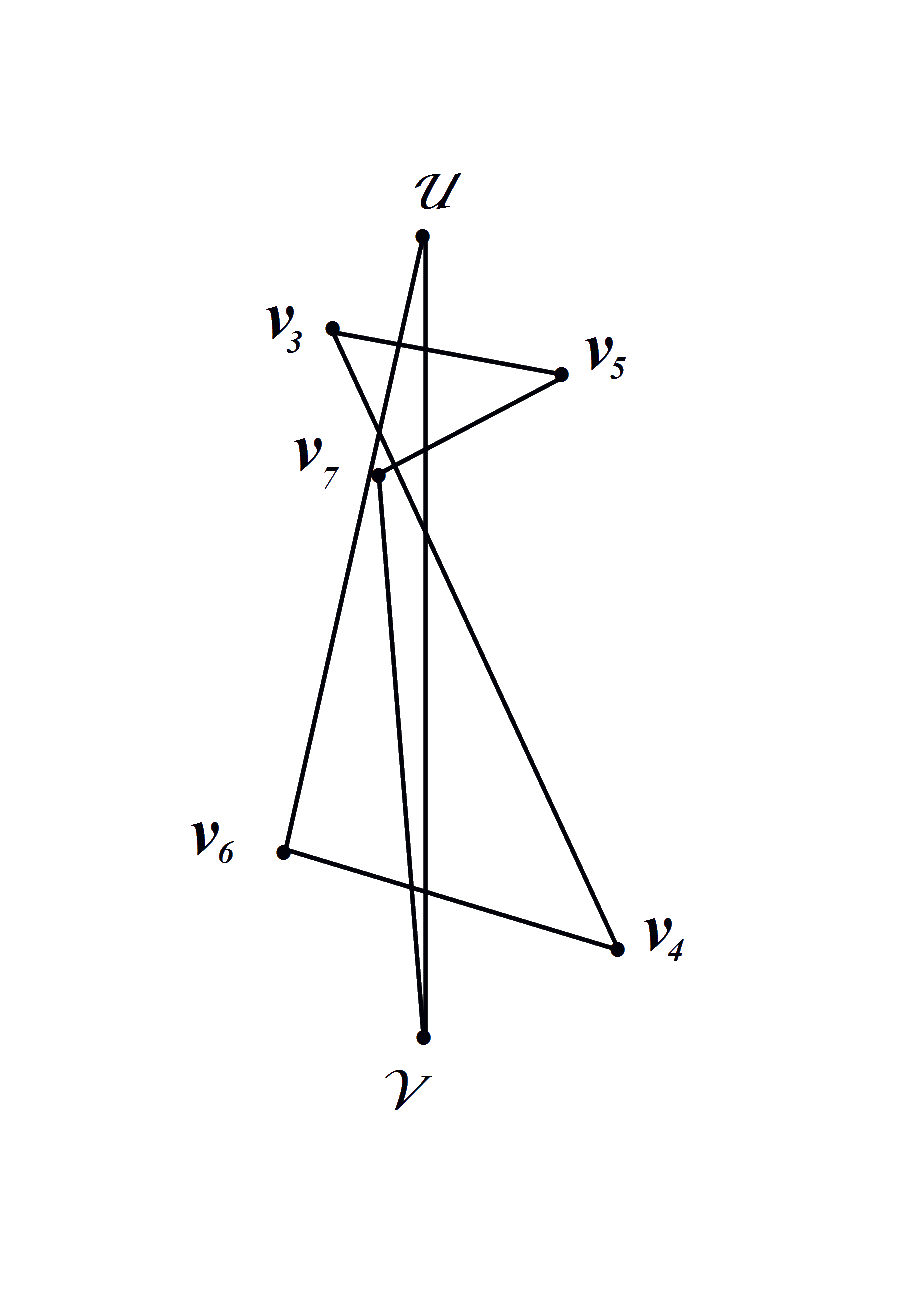
Рис.1 Рис.2
Из Рис.2 видно, что на первом и втором этапах построения из цикла исключается ребро En = diam(G ). В результате на Рис.2 был построен цикл Гамильтона, состоящий из четырёх вершин.
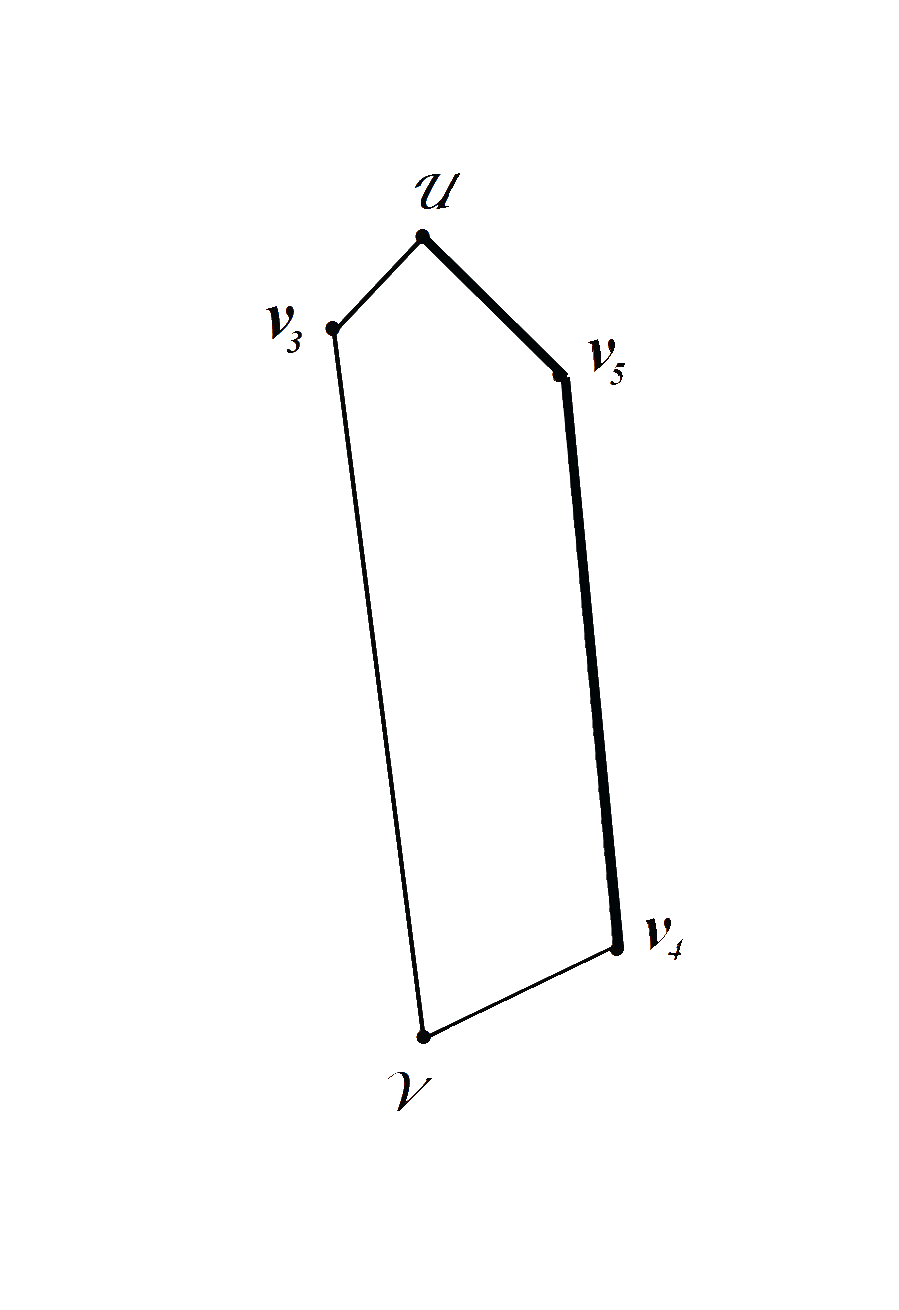
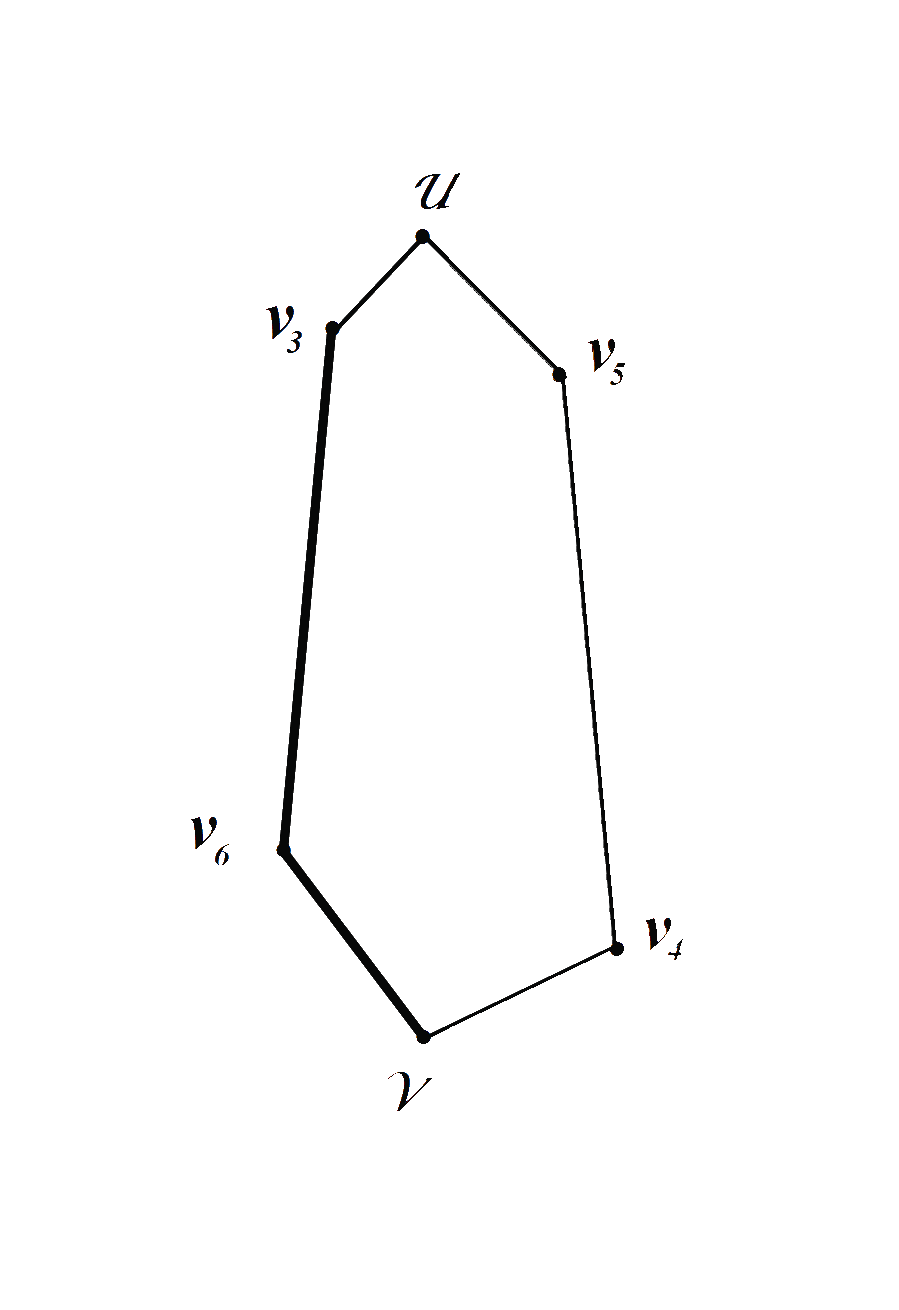
На следующих двух этапах построения определяем очередную вершину V5, следующую за вершиной V4, по максимальной удалённости от одного из полюсов графа и очередную вершину V6, следующую за вершиной V5, так же по максимальной удалённости от одного из полюсов графа. Затем соединяем новые вершины аналогично предыдущему этапу построения с ближайшими к ним рёбрами соответственно из предыдущего цикла. Сначала с ближайшей вершиной из предыдущего цикла, а затем с вершиной того же ближайшего ребра, максимально удалённой от полюса графа ближайшего к этой же очередной новой вершине, соответственно.
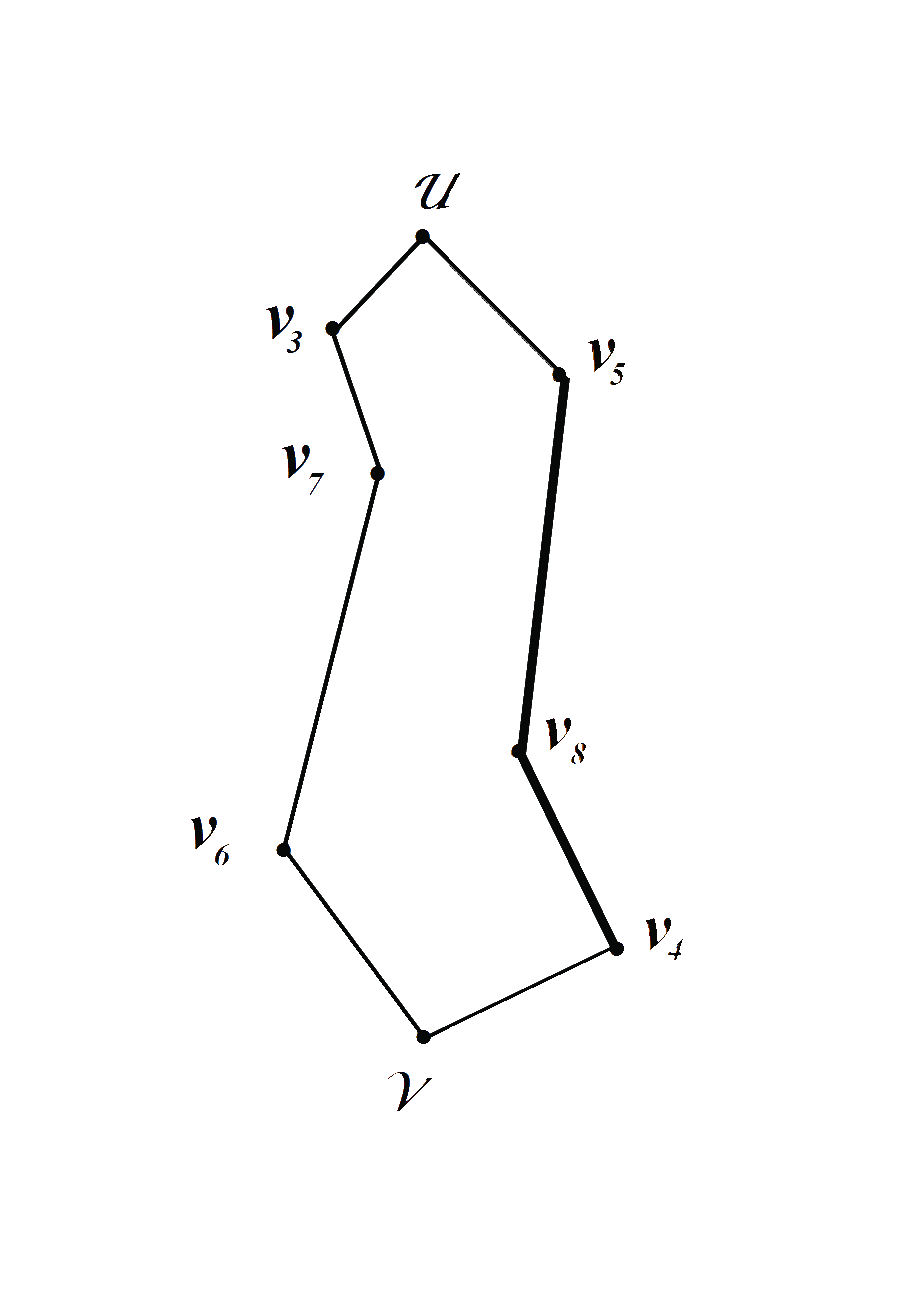
Рис.3 Рис.4
Из Рис.4 видно, что на третьем и четвёртом этапах построения из цикла исключаются рёбра ближайшие к новым очередным вершинам V5 и V6. В результате был построен цикл Гамильтона, состоящий из шести вершин, Рис.4.
На следующих этапах все построения проводятся аналогично предыдущим этапам для любого количества новых очередных вершин |Vm|. В результате будет построен цикл Гамильтона, состоящий из всех заданных вершин |Vm| и по величине, состоящий из множества рёбер |Ek | из |En | .
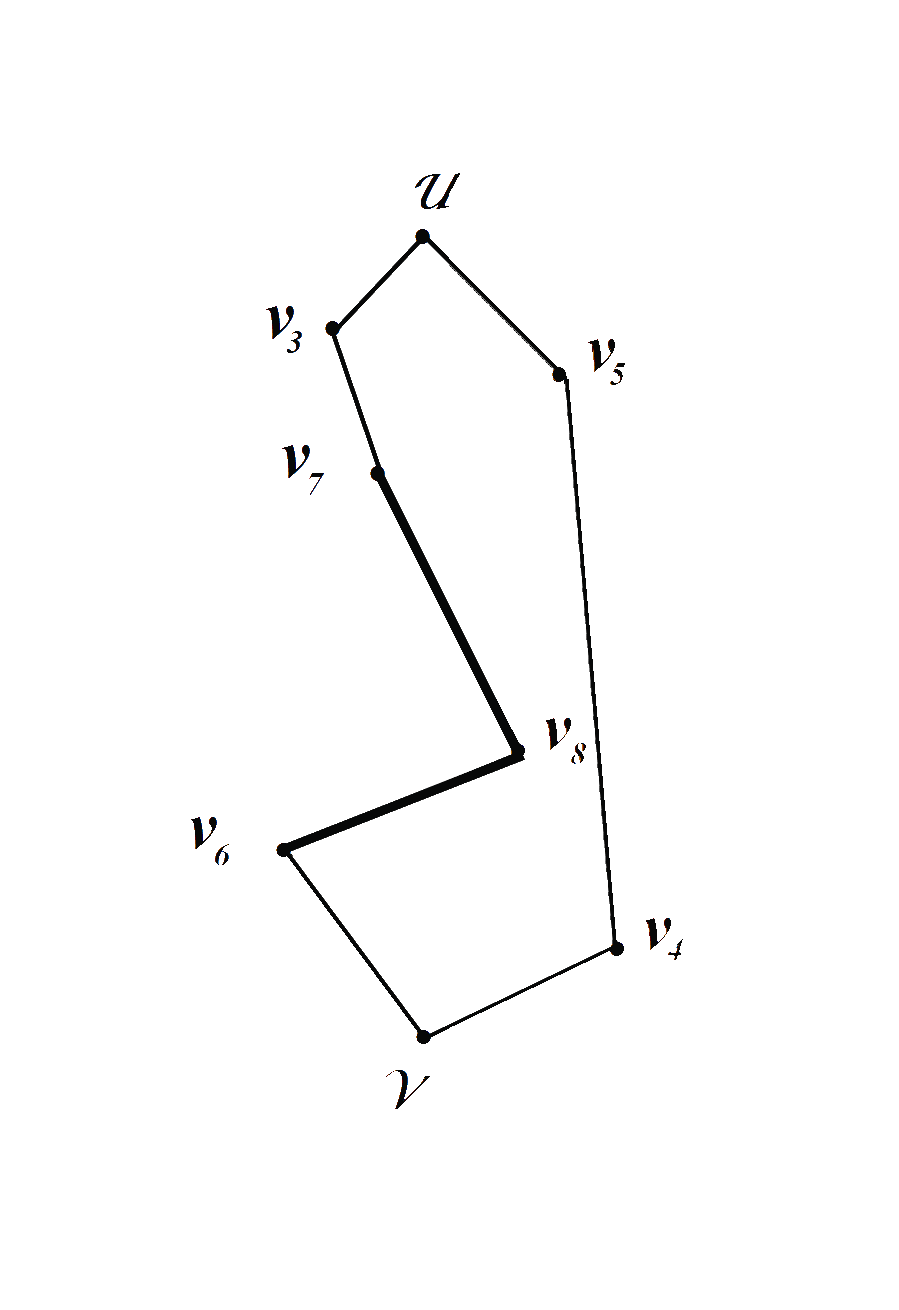
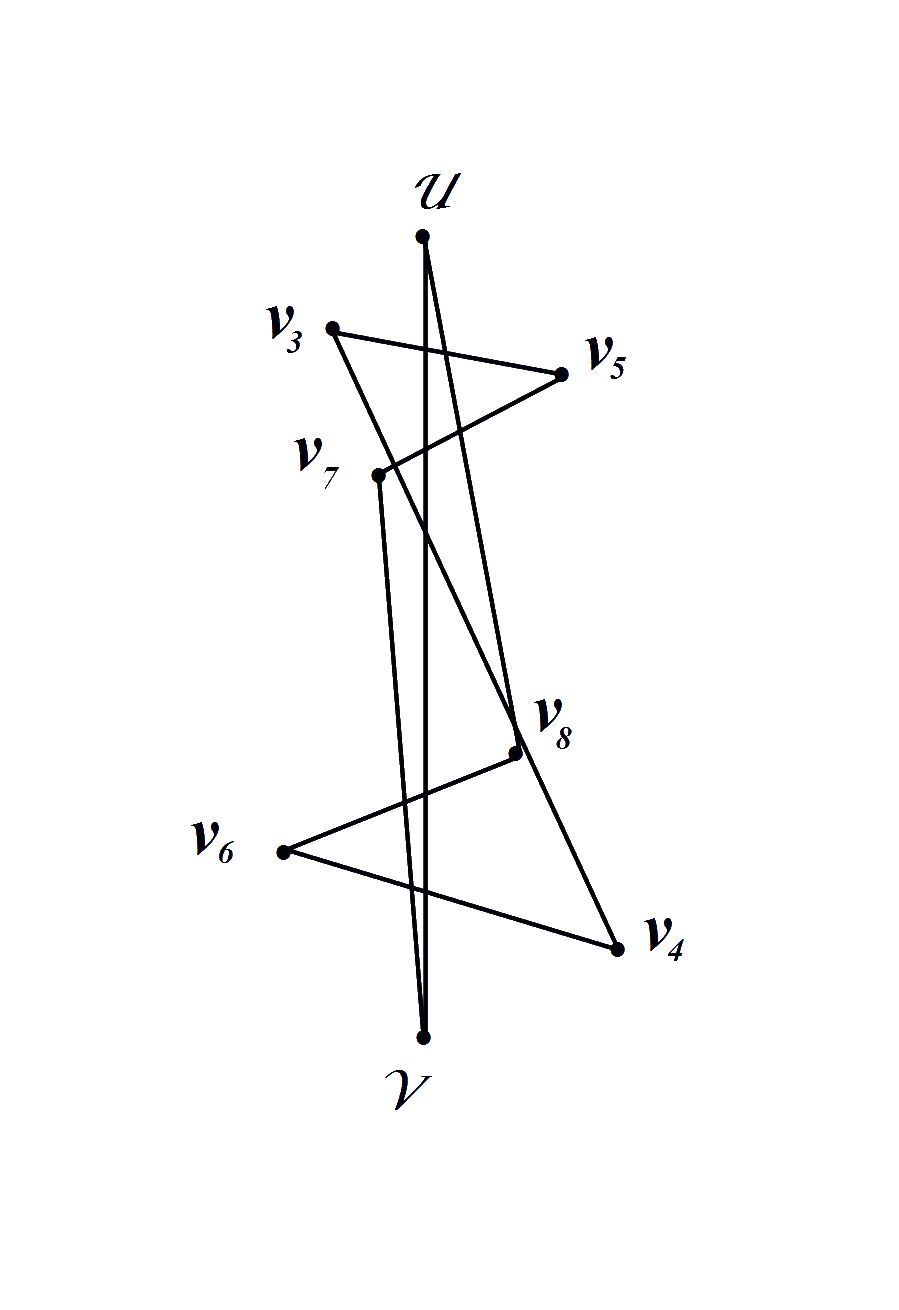
Рис.5 Рис.6
На Рис.6 построен цикл Гамильтона, состоящий из восьми вершин.
Таким же методом можно построить последовательность всех циклов Гамильтона, начиная от минимального и далее следующих по увеличению. Для этого на каждом новом этапе построения необходимо каждую новую очередную вершину соединять с вершиной из предыдущего цикла, которая будет следующей ближайшей к этой же очередной вершине, то есть с ребром из предыдущего цикла следующим сразу за ребром ближайшим к очередной новой вершине.
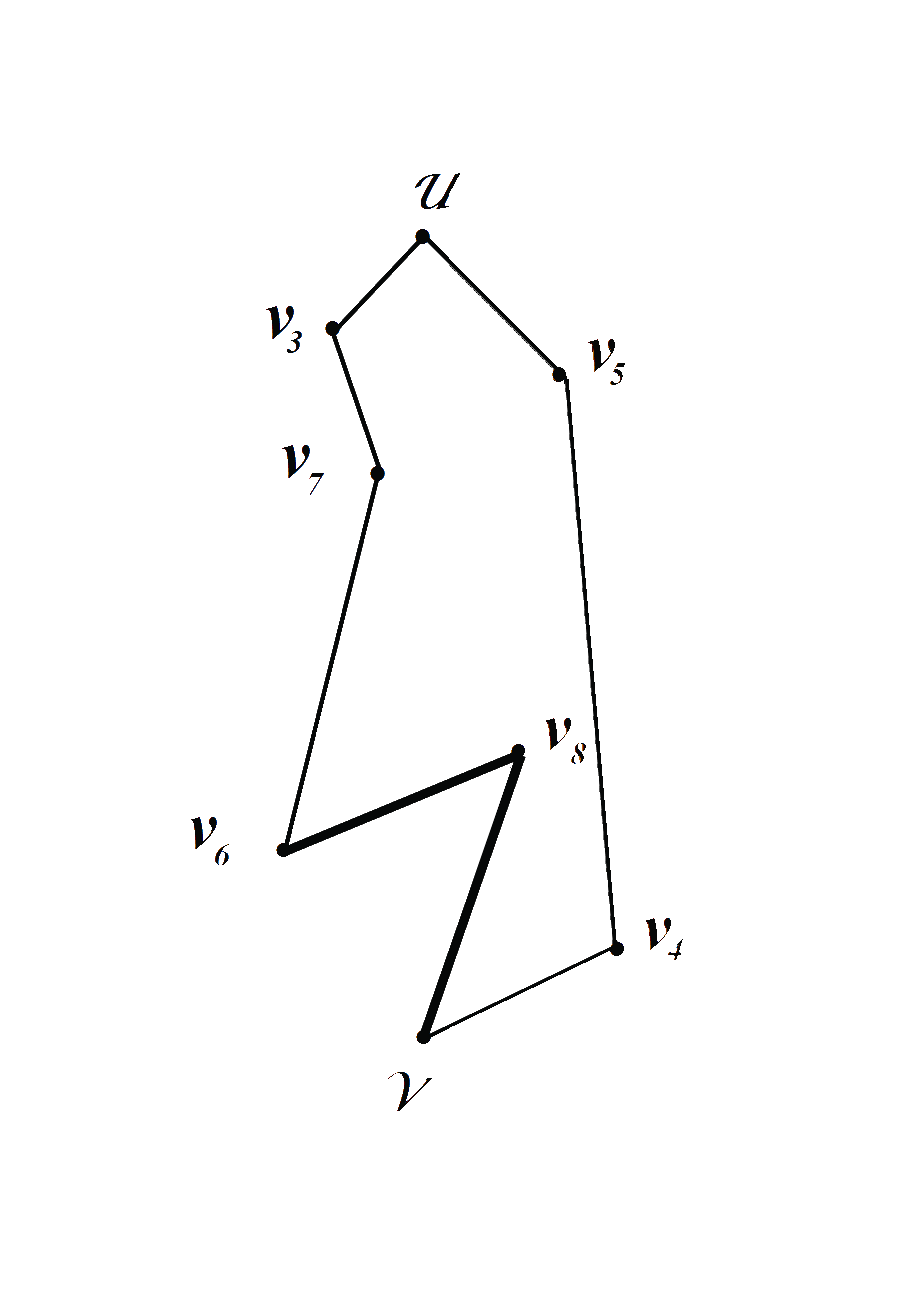
Рис.7 Рис.8
На рисунках Рис.7 и Рис.8 построены два элементарных цикла, следующих по очереди за минимальным циклом Гамильтона по увеличению величины |E | .
|Ek | < |Ek-1| < |Ek-2 | (7)
Построение максимального цикла Гамильтона
Аналогичным, описанному выше, методом возможно построить так же и максимальный цикл Гамильтона. Для этого будем выбирать каждую очередную новую вершину, как максимально удалённую от одного из полюсов графа, аналогично. Далее необходимо эту очередную верщину соединять с максимально удалённым от неё ребром из предыдущего цикла. Одна из вершин такого максимально удалённого ребра будет находиться на максимальном расстоянии от этой очередной новой вершины, а вторая вершина того же ребра будет ближайшей к тому полюсу графа, который максимально удалён от этой же очередной новой вершины.
Рис.9 Рис.10
На рисунке Рис.9 построен максимальный цикл Гамильтона, состоящий из семи вершин. На рисунке Рис.10 построен максимальный цикл Гамильтона, состоящий из восьми вершин, включая оба полюса графа.
Упрощение построений
Построение элементарного цикла или цикла Гамильтона, минимального или максимального, возможно упростить, если вместо диаметра графа diam(G ) рассматривать радиус графа radius(G ). Тогда вместо расстояний между вершинами и полюсами графа в построении будут участвовать расстояния между вершинами и мнимым центром диаметра графа.
Общие выводы
На каждом этапе построения выполняется один и тот же алгоритм выбора SelAlg, который включает в себя одни и те же три функции выбора selF(V,E ). Функция выбора диаметра графа selF(diam(G )) выполняется только один раз на первом этапе построения.
SelAlg(V,E ) = (selF1(Emax,Vk+1,V,U);selF2(Emin,Vk+1,Vk-i);selF3(Emax,Vk+1,Vk-j))
(i , j ) = 0,1,2,3, . . (8)
Из определения (8) следующая функция:
selF1(Emax,Vk+1,V,U) есть функция выбора очередной новой вершины из множества заданных вершин |V | .
Следующая последовательность функций из определения (8) :
selF2(Emin,Vk+1,Vk-i);selF3(Emax,Vk+1,Vk-j) определяет порядок выбора ближайшего ребра к этой очередной вершине Vk+1, которая в свою очередь состоит из двух функций, сдедующей функции выбора некоторой ближайшей вершины Vk-i из предыдущего цикла к этой очередной вершине Vk+1
selF2(Emin,Vk+1,Vk-i) и следующей функции выбора вершины Vk-j, которая максимально удалена от полюса графа, который в свою очередь является, напротив, ближайшим к этой очередной вершине Vk+1, и принадлежит тому же ближайшему ребру
selF3(Emax,Vk+1,Vk-j)
Количество элементарных шагов выбора для функции selF1 и функции selF2 не превышает степени |V | с показателем два
|steps:(selF1,selF2)| < |V |2 (9)
И количество элементарных шагов или операций выбора для функции selF3 не превышает двух
|steps:(selF3)| = 2 (10)
Количество шагов или этапов построения минимального цикла Гамильтона для алгоритма выбора selAlg(C (V,E )) равно количеству заданных вершин |V |, исключая две вершины, которые определяют Emax или диаметр графа
|steps:SelAlg(Cmin(V,E )) | = |Vm ̶ 2| (11)
Таким образом задача построения минимального цикла Гамильтона R(Cmin(V,E )) принадлежит классу P полиномиальных задач
P:includes:R(Cmin(V,E )) (12)
Это утверждение справедливо и для максимального цикла Гамильтона
P:includes:R(Cmax(V,E )) (12)1
Литература:
- Гэри М., Джонсон Д. Вычислительные машины и трудно решаемые задачи. ̶М.: Мир, 1982.
- Лорьер Ж.-Л. Системы искусственного интеллекта. ̶ М.: Мир, 1991. ̶ 568 c.