Введение. Задачи на графах находят применение в различных областях, связанных с самым широким спектром математических методов для анализа происходящих там процессов. В настоящее время описаны эффективные методы и алгоритмы решения таких задач, они приводятся в научной и учебной литературе. Разработаны пакеты прикладных программ, позволяющих решать ряд стандартных вопросов, например, задачи о покрытии графов, о раскрасках, об изоморфизме графов. Применение этих пакетов разумно, оправдано и вполне возможно без знания алгоритмов решения задач и технологий, обеспечивающих реализацию алгоритмов. В то же время теоретические исследования позволяют модернизировать и использовать более эффективно разработанные пакеты.
В связи с этим целью данной работы является выработка комбинированного подхода к решению задач на графах, использующего как численные схемы и методы, так и теоретические положения. Исследуется вопрос о гамильтоновости неориентированных кубических графов, являющихся объединениями двух циклов длины n и соединяющих их боковых ребер. Формулируются гипотезы о существовании гамильтонова цикла в заданном кубическом графе. Приводится описание и результаты работы вычислительного алгоритма для проверки сформулированных гипотез.
1. Основные определения. Графом G называется пара (V(G),E(G)), где V(G) –непустое конечное множество элементов, называемых вершинами, 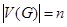 , а E(G) –конечное семейство неупорядоченных пар элементов из V(G) (не обязательно различных), называемых ребрами,
, а E(G) –конечное семейство неупорядоченных пар элементов из V(G) (не обязательно различных), называемых ребрами, 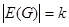 . Будем рассматривать далее симметричный неориентированный граф без петель, кратных ребер и изолированных вершин.
. Будем рассматривать далее симметричный неориентированный граф без петель, кратных ребер и изолированных вершин.
Обозначим через 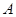 матрицу смежности графа,
матрицу смежности графа,
|
|
если существует ребро, соединяющее вершину |
|
в других случаях, |
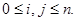
Маршрутом в графе G называется конечная последовательность ребер вида 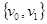 ,
,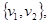 …
…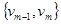 , такая, что
, такая, что 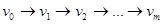 .
.
Маршрут называется цепью, если все его ребра различны, и простой цепью, если различны все вершины. Цепь или простая цепь замкнуты, если 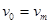 . Замкнутая простая цепь, содержащая, по крайней мере, одно ребро, называется циклом.
. Замкнутая простая цепь, содержащая, по крайней мере, одно ребро, называется циклом.
Цикл, проходящий через каждую вершину один раз, называется гамильтоновым. Граф, содержащий такой цикл, называется гамильтоновым графом.
Пусть G конечная группа S G\{1} , тогда
Г(G,S)– граф Кэли
V(Г)=G - множество вершин
E(Г)= 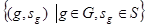 - множество ребер.
- множество ребер.
2. Условия существования гамильтонова цикла в графе. Сформулируем без доказательства достаточные условия существования гамильтонова цикла в n-вершинном неориентированном графе [8, 10].
Теорема Оре. Если 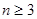 и для любой пары
и для любой пары 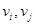 несмежных вершин выполнено условие
несмежных вершин выполнено условие 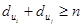 , то гамильтонов цикл существует (
, то гамильтонов цикл существует (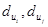 - степени вершин
- степени вершин 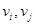 ).
).
Теорема Дирака. Если 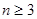 и для любой вершины
и для любой вершины 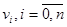 , выполнено условие
, выполнено условие 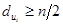 , то гамильтонов цикл существует.
, то гамильтонов цикл существует.
Под кубическим графом будем понимать граф, степень каждой вершины которого равна трем.
Кубические графы, полученные из двух циклов одинаковой длины, соединенных боковыми ребрами, обозначим через 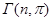 , где
, где 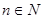 , а
, а 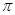 определяет подстановку вида:
определяет подстановку вида: 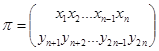 .
.
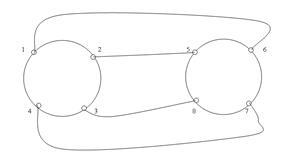
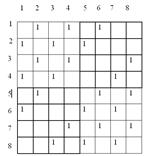
На рис.1,2 изображен кубический неориентированный 8-вершинный граф и соответствующая ему матрица смежности.
|
|
|
|
Рис.1 |
Рис. 2 |
Может быть показана справедливость следующего утверждения:
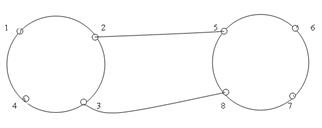
Лемма. В графе существует гамильтонов цикл с двумя боковыми ребрами тогда и только тогда, когда существуют два боковых ребра, соединяющих смежные вершины в долях.
Рисунок 3 иллюстрирует указанный случай.
|
|
|
Рис. 3 |
Рассмотрение широкого круга частных случаев кубических графов позволяет автору сформулировать две гипотезы:
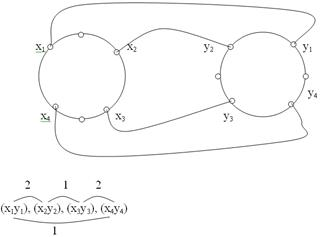
Гипотеза 1. Пусть дан граф Г(n,π). Обозначим боковое ребро парой 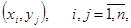 n є N. Граф Г(n,π) гамильтонов тогда и только тогда, когда пары можно упорядочить следующим образом:
n є N. Граф Г(n,π) гамильтонов тогда и только тогда, когда пары можно упорядочить следующим образом: 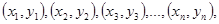 где первая и вторая пары - смежные по первой координате в
где первая и вторая пары - смежные по первой координате в 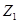 или по второй координате в
или по второй координате в 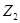 ,, вторая и третья пары - смежные по другой координате, соответственно, в
,, вторая и третья пары - смежные по другой координате, соответственно, в 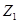 или
или 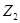 , и т.д. Далее чередуются координаты и соответствующие им доли, а последняя по выпавшей очередности - смежная с одной из координат первой пары.
, и т.д. Далее чередуются координаты и соответствующие им доли, а последняя по выпавшей очередности - смежная с одной из координат первой пары.
Представим утверждение сформулированной гипотезы графически (см.рис.4.)
|
|
|
Рис. 4 |
Гипотеза 2. Если Г(n,π) гамильтонов, то он содержит гамильтонов цикл с количеством боковых ребер ≤ n/2 в случае, если n четно, и с количеством боковых ребер ≤(n/2)-1, в противном случае.
3. Описание алгоритма. Для проверки сформулированных гипотез разработан и реализован вычислительный алгоритм. Результатом работы алгоритма является ответ на вопрос, является ли кубический граф, удовлетворяющий условию гипотезы 1, гамильтоновым. Далее, удовлетворяет ли заданный гамильтонов кубический граф условиям гипотезы 2. Итерация алгоритма поиска гамильтонова цикла в графе основана на значительном сокращении количества перебираемых вариантов. Для иллюстрации алгоритма рассмотрим матрицы смежности 6-вершинных кубических графов, представленные на рис.5.
|
|
|
Рис. 5 |
На рис. 5 черным цветом обозначены ячейки матицы, которые при данном положении элемента «1»должны быть пустыми. В одной колонке или строке элемента «1» не могут быть еще клетки с «1», т.к. в этом случае степень вершины будет больше трех, а граф, который мы рассматриваем, кубический. В том случае, если мы расположим «1» в других клетках, помеченных черным цветом, то получим гамильтонов цикл, т.к. этот случай удовлетворяет условию, когда в графе Г(n,π)существуют смежные вершины одной доли, соединенные с двумя смежными вершинами другой доли.
Программное обеспечение разработано в среде Borland Delphi 7. В результате работы алгоритма показано, что условия сформулированных гипотез 1,2 для случаев 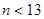 выполнены. Указанный подход на примере рассмотрения кубических неориентированных графов расширяет круг методов решения задач, связанных с исследованием вопросов о гамильтоновости графов.
выполнены. Указанный подход на примере рассмотрения кубических неориентированных графов расширяет круг методов решения задач, связанных с исследованием вопросов о гамильтоновости графов.
Литература.
1. Roberts S. M., Flores B. An engineering approach to the traveling salesman problem. Man. Sci.- 1967.
2. Roberts S. M., Flores B. Systematic generation of Hamiltonian circuits, Comm. of ACM, № 9.- 1966.
3. Берж К. Теория графов и ее применения. — М.: Издательство иностранной литературы.- 1962.
4. Давыдов Э.Г. О конечных графах и их автоморфизмах. Сб. «Проблемы кибернетики». Вып.17. –М.: Физматгиз. – 1966.
5. Дистель Р. Теория графов. – Новосибирск: Институт математики СО РАН.- 2002.
6. Емеличев В.А., Мельников А.И., Сарванов В.И., Тышкевич Р.И. Лекции по теории графов. – М.:Наука.- 1990.
7. Зыков А.А. Основы теории графов. – М.: Вузовская книга.- 2004.
8. Кристофидес Н. Теория графов: алгоритмический подход.- М.: Мир.- 1978 .
9. Носов В.А. Комбинаторика и теория графов.- М.: МГТУ.- 1999.
10. Оре О. Теория графов. –М.: Наука.- 1982.
11. Харари Ф. Теория графов. — М.: Мир.- 1973.
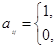
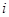 и вершину
и вершину 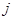 ,
,