В статье рассматривается эффективность метода полного перебора при поиске минимального покрывающего подмножества вершин на неориентированном графе.
Ключевые слова: неориентированный граф, полный перебор, зависимость времени счета от количества вершин, теория графов.
Значимость исследований в данной области определяется тем, что результаты могут быть использованы на информатике, математике, геометрии, при строительных работах, черчении. Также они могут быть внедрены непосредственно в практическую деятельность, так как теория графов находит применение, например, в геоинформационных системах (ГИС). Существующие или вновь проектируемые дома, сооружения, кварталы и т. п. рассматриваются как вершины, а соединяющие их дороги, инженерные сети, линии электропередачи и т. п. — как рёбра. Применение различных вычислений, производимых на таком графе, позволяет, например, найти кратчайший объездной путь или ближайший продуктовый магазин, спланировать оптимальный маршрут.
Цель работы: выяснить особенности применения теории графов при решении задач и в практической деятельности; экспериментальное определения эффективности применения поиска полным перебором минимального покрывающего подмножества вершин на неориентированном графе.
Вводная часть: неориентированный граф . Неориентированный граф G — это упорядоченная пара G: = (X, U), для которой выполнены следующие условия: X — это множество вершин или узлов, U — это множество неупорядоченных пар различных вершин, называемых рёбрами. Т. е. в неориентированных графах можно двигаться в обе стороны [1]. Вершины и рёбра графа называются также элементами графа, число вершин в графе | X | — порядком, число рёбер | U | — размером графа. Полный перебор (или метод «грубой силы» от англ. brute force) — метод решения задачи путем перебора всех возможных вариантов. Сложность полного перебора зависит от размерности пространства всех возможных решений задачи. Если множество решений очень велико, то полный перебор может не дать результатов в течении длительного времени. Идея полного перебора сводится к следующему: перебираются всевозможные решения и из них выбирается решение (или множество решений) отвечающее условию задачи [2]. Если стоит задача поиска минимального вершинного покрытия, соответственно, требуется из всевозможных вариантов объезда пунктов выбрать маршрут, позволяющего минимальному количеству вершин обойти все остальные вершины.
Пример возможной постановки задач и поиска. На множестве вершин Х заданного графа G(X,U) требуется выбрать такое подмножество Х’, для которого справедливо: из любой i-й вершины подмножества Х’ существует дуга (i,j) ϵ U, где j — индекс вершины в подмножестве X\X’; в любую вершину j-ю подмножества X\X’ заходит хотя бы одна дуга (i,j) ϵ U такая, что i-я вершина принадлежит подмножеству X’; │X’│→min [3].Формальная постановка задачи будет основана наследующих обозначениях: G(X, U) — взвешенный орграф; X — множество вершин;
U — множество дуг; A(G) — множество контуров графа; a
k
—
k — й контур множества A(G); X(a
k
) — множество вершин k — го контура; U(a
k
) — множество дуг k — го контура; r(i, j) — вес дуги (i, j)
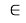
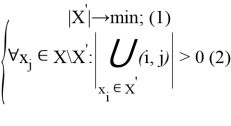
Условие (1) утверждает, что выбранное подмножество вершин X’ должно быть минимальным. Условие (2)- в любую вершину j-ю подмножества X\X’ заходит хотя бы одна дуга (i,j) ϵ U такая, что i-я вершина принадлежит подмножеству X’. Таким образом, на основе описанного выше можно составить следующий алгоритм: шаг 1- полученный граф G(X,U); шаг 2- методом полного перебора обходим граф и заносим данные в стек; шаг 3- если вершины не покрывают граф и длина такого пути равна ∞, то путь невозможен; шаг 4- среди данных стека находим маршрут с минимальным количеством вершин, для сортировки используем функцию key (является “аргументом” для сортировки, значением, которое используется для сравнения); шаг 5- выводим матрицу смежности исходного неориентированного графа; шаг 6- выводим вес и вершины.
Экспериментальное обоснование. Изучим зависимость времени выполнения программы от количества вершин в заданном графе и от числа дуг (ребер) графа при фиксированном числе вершин. Для этого воспользуемся модулем time на основе выведенного программного кода (рис.1).
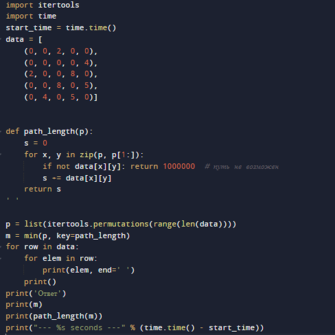
Рис. 1. Программный код
На основе полученных данных вывели зависимость времени счета от количества вершин (рис. 2). Также для сравнения вывяли зависимости времени счета от числа дуг (ребер) графа при фиксированном числе вершин (рис. 3). В качестве фиксированного числа взяли 7 вершин. Полученные результаты указывают на экспоненциальную зависимость времени поиска решения от размерности задачи. Эта зависимость говорит о том, что полный перебор- неэффективный метод решения поставленных задач.
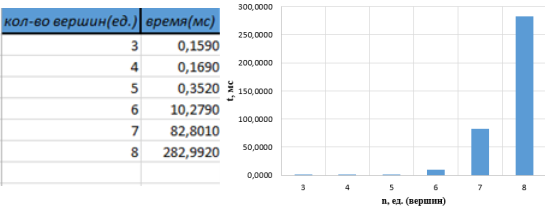
Рис. 2. Таблица и гистограмма зависимости времени счета от количества вершин
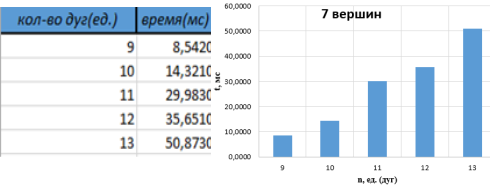
Рис. 3. Таблица и гистограмма зависимости времени счета от числа дуг (ребер) графа при фиксированном числе вершин (7 вершин)
Заключение. Таким образом, основываясь на полученных данных, полный перебор- неэффективный метод решения поставленных задач в данной области, т. к. время поиска им решения экспоненциально зависит от размерности задачи. Из проделанной работы можно сделать вывод, что полный перебор зависит от количества всех возможных решений задачи и затрачивает длительный промежуток времени при большом пространстве решений. Это указывает на то, что следует продолжать исследования других методов поиска как минимального покрывающего подмножества, так и других необходимых значений в данной области.
Литература:
- Берж К. Теория графов и ее применения. М.: Иностранная литература, 1962. — 319 с.
- Кристофидес Н. Теория графов. Алгоритмический подход. М.: Мир, 1978, — 432 с.
- Python Cookbook: Recipes for Mastering Python 3 Книга, Дэвид М. Бизли.

