Наш современный мир наполнен не только буквами разных языков и цифрами различных видов, но и изображениями, представленными в многочисленных интерпретациях: всевозможные фотографии, картины всех эпох и стилей, а также такие вещи как схемы. Схемы встречаются на логотипах компаний и автомобилей, картах и дорожных знаках, строительных схемах и учебниках по информатике, в математике им даже посвящен отдельный раздел изучения и так далее.
Попробуйте вспомнить карту метро или электричек. Вы представляете набор цветных линий (направлений маршрутов) и точек на пересечении этих линий с подписями (станции метро или вокзалов), не так ли? Так вот это один из простейших и наиболее узнаваемых примеров таких схем как графы. Именно о них пойдет речь в нашей работе.
В данной статье вы узнаете насколько полезны порой бывают графы, и что благодаря своей, на первый взгляд, простоте они нашли применение во многих областях нашей жизни.
По мимо всего это мы затронем немного истории графов и узнаем о Леонарде Эйлере, который дал толчок развитию теории графов, а также узнаем ученых, которые внесли огромный вклад в изучении графов.
Мы рассмотрим различные задачи, решение которых становится простым и более быстрым благодаря графам. Поймем, как графы помогают в оптимизации маршрутов (как раз один из примеров оптимизации маршрутов движения вы сами уже в начале вспомнили), для чего используют графы при строительстве любых зданий и какова может быть взаимосвязь между графами и всем известными геометрическими фигурами, однако мы успеем затронуть не все темы, в которых можно заметить участие графов…
Нам хотелось бы, чтобы эта статья, помогла понять насколько важны графы, и чтобы они стали частью вашего восприятия мира.
Начнем наш рассказ и параллельно исследование графов, как и любой другой темы во многих предметах – с истории. Родоначальником теории графов принято считать математика Леонарда Эйлера (1707-1783). Однако теория графов многократно переоткрывалась разными авторами при решении различных задач.
Издавна среди жителей Кёнигсберга была распространена такая загадка: как пройти по всем городским мостам (через реку Преголя), не проходя ни по одному из них дважды.
В 1736 году задача о семи мостах заинтересовала выдающегося математика, члена Петербургской академии наук Леонарда Эйлера. Эйлер пишет о том, что он смог найти правило, пользуясь которым, легко определить, можно ли пройти по всем мостам, не проходя дважды ни по одному из них. В данном случае ответ был: «нельзя».
Эйлер представил эту часть города в упрощенном виде – графе, где мостам соответствуют линии (ребра графа), а частям города — точки соединения линий (вершины графа).
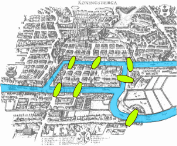

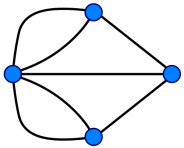
Рис. 1 Задача Эйлера
Азы теории графов
Граф – это множество точек, которые также могут называть вершинами или узлами графа, и множество ребер или же дуг графа, которые попарно соединяют вершины.
Если мы назовем или отметим какими-либо знаками вершины графа, то он будет называться помеченным (например, ветки метро с помеченными названиями станций узлами).
Графы могут быть ориентированными, если задать показать (чаще всего простой стрелочкой) в ребре от какой вершины к какой идет направление. А если мы подпишем какое-либо значение (веса), то такой граф будет называться взвешенным. А если направление не задано, то граф, соответственно, называется – неориентированным. Если все ребра в графе являются ориентированными, то такой граф можно называть – орграфом. На пример взвешенного ориентированного графа международных торговых отношений.
Графы имеют множество представлений. Их можно показать, как в графическом виде, так и таблицей или списком. Вершины графа можно изображать в виде точек, окружностей, треугольников, а ребра прямыми отрезками либо же фигурно изогнутых линий. Существует такое понятие как изоморфные графы. Это такие графы, которые эквивалентны друг другу, но выглядят по-разному.
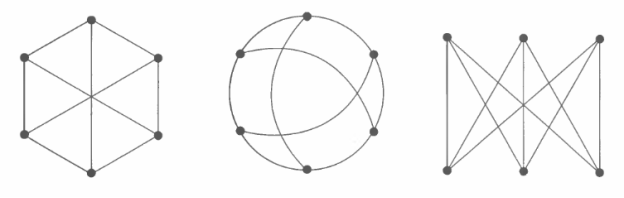
Рис.2 Три фигуры – три изоморфных представления одного и того же графа
Примеры встречи графов в жизни
Опять же предлагаю вернуться ко всем известному примеру – схема транспортных путей. Графы на таких схемах очень четкие, чтобы можно было видеть не только сами маршруты, но и переходы между ними. Впервые графы были применены на схемах метро в лондонском метрополитене.
Ниже вы можете увидеть на примере нашего города графы-схемы транспортных путей маршруток 55 и 75 соответственно.
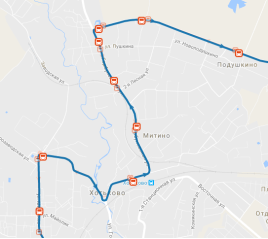
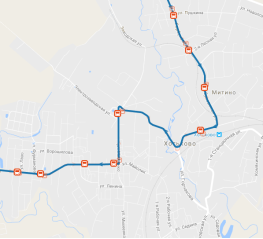
Рис. 3 Графы-схемы транспортных путей маршрутных такси № 55 и № 75
Также не менее известных пример графов – это иерархические деревья. В пример иерархических графов будет интересна, например, иерархия администрации г/п Хотьково:
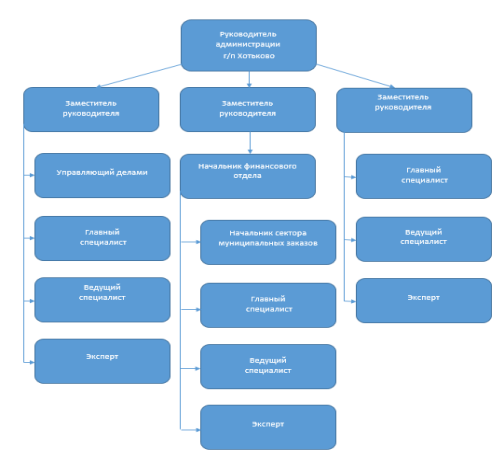
Рис.4 Иерархия администрации г/п Хотьково
В наше время многие из нас, если не все, встречались со словосочетанием «Компьютерная сеть» или «Сеть Интернет». Так вот эти сети также можно показать в виде графа. WWW – WorldWideWeb – Всемирная Паутина или же попросту Интернет и есть один большой граф в виде паутины, растянутой по всему миру. В наше время многие из нас, если не все, встречались со словосочетанием «Компьютерная сеть» или «Сеть Интернет». Так вот эти сети также можно показать в виде графа. WWW – WorldWideWeb – Всемирная Паутина или же попросту Интернет и есть один большой граф в виде паутины, растянутой по всему миру.
Нередко графы можно встретить, например, в химии. Там, графы представляют особый интерес при изучении структуры молекул. Сложную структуру молекулы или изомера удобно представить в виде самого простого графа, что помогает понять связи между атомами молекулы.
Помимо всех замудреных вещей в науке, строительстве, транспорте, некоторые люди додумались создавать небольшие игры, в создании или решении которых присутствуют графы.
Например, достаточно сложная, а точнее требовательная к терпению и внимательности задачка Мартина Гарднера. На сетке размерами 7х7 клеток (рис. 19) нужно провести вдоль линий сетки 5 непересекающихся линий так, чтобы соединить точки, обозначенные одинаковыми буквами.
Рис. 5 Задача Гарднера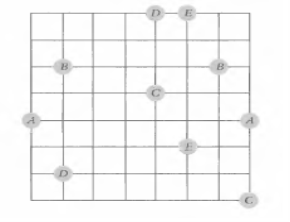
Нашей статьей мы хотели донести такую мысль, что если эта тема вас заинтересовала, то не прекращайте поиски, а продолжайте ее изучать. Существует множество книг, связанных с теорией графов и смежных ей областях – типологии, теории алгоритмов, дискретной математике и многих других.
Нам бы хотелось, чтобы вам запомнилась идея, доказательством которой служит теория графов: с помощью удивительно простых схем, состоящих из линий и точек, можно описать и решить множество разнообразных задач.
Литература
- Оре О. Теория графов. — М.: Наука, 1968. — 336 с.
- Уилсон Р. Введение в теорию графов. — М.: Мир, 1977. — 208 с.
- Харари Ф. Теория графов. — М.: Мир, 1973.
- Кормен Т. М. и др. Часть VI. Алгоритмы для работы с графами // Алгоритмы: построение и анализ | Introduction to Algorithms. — 2-е изд. — М.: Вильямс, 2006. — С. 1296.
- Салий В. Н., Богомолов А. М. Алгебраические основы теории дискретных систем. — М.: Физико-математическая литература, 1997.

