Рассматривается система интегро-дифференциальных уравнений
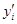
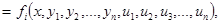
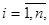(1)
где
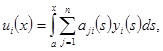
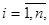(2)
и функции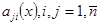 
дифференцируемы. Ищется решение 
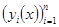системы (1), удовлетворяющие интегральным условиям.
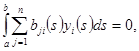
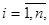(3)
причем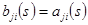 
при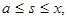 
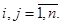
Введем новые неизвестные функции равенствами
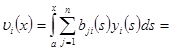
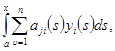
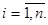(4)
Дифференцируя обе части (4) по х, имеем
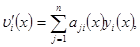
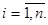(5)
Предположим, что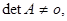 
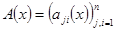. Тогда из (5) находим
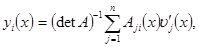
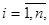(6)
где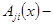 
алгебраические дополнения элементов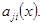 
Продифференцируем еще раз равенства (5).
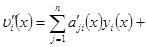
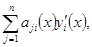
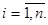(7)
С учетом системы (1), равенств (2) и формул (6), (7) получим
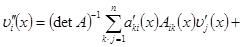
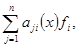
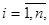(8)
где
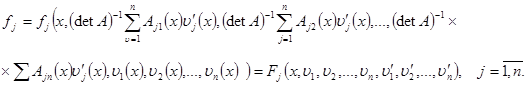(9)
Такую систему (8) можно записать в виде
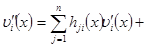
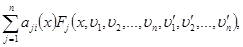
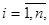(10)
если положить
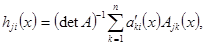
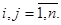(11)
Имея (2) и (3) для системы (10) получаем граничные условия
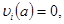
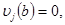
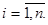(12)
Таким образом задача (1), (3) свелась к двухточечной задаче для системы дифференциальных уравнений второго порядка, которая изучена в известных работах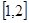 
.
Литература.
1. Исраилов С.В., Юшаев С.С. Многоточечные и функциональные краевые задачи для ОДУ. Нальчик.: «Эль-Фа». 2004.. С.440
2. Ешуков Л.Н., Веков С.С. и др. Проблемы и библиография теории краевых задач обыкновенных дифференциальных уравнений. // Тр. Рязанского радиотехнического института. 1972. Вып. 42. С. 164-192.
