Введение. Постановка задачи.
Псевдослучайные последовательности используются для генерации секретных ключей шифрования, для вычисления цифровой подписи и для работы многих алгоритмов аутентификации. Для построения псевдослучайных последовательностей используются линейные рекуррентные последовательности на эллиптической кривой.
Поставим задачу проанализировать существующие генераторы на эллиптической кривой и разработать генератор псевдослучайных последовательностей на эллиптической кривой с использованием квадратичных полей Галуа.
Анализ генераторов построенных на точках эллиптической кривой
Генератор псевдослучайных последовательностей должен удовлетворять следующим двум требованиям, предложенным в работе []:
- Статистической безопасностью: последовательность, созданная генератором псевдослучайных чисел должна статистически ничем не отличаться от абсолютно случайной последовательности.
-
Криптографической
безопасности: возможности зная
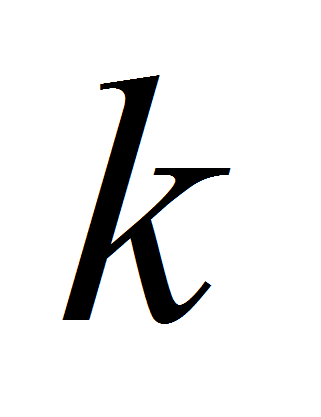 -битов
последовательности, предсказать следующий или
-битов
последовательности, предсказать следующий или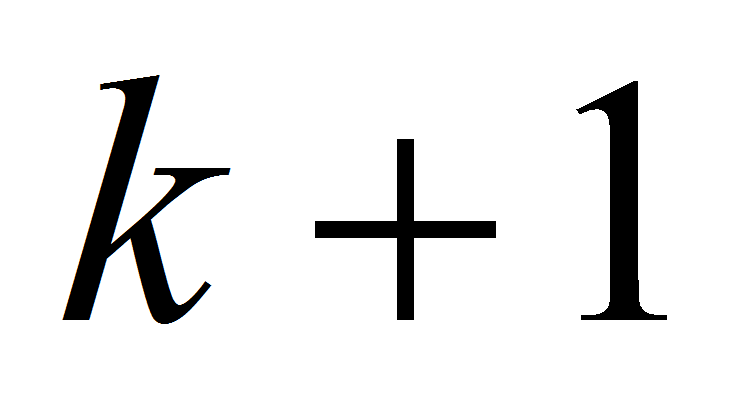 -бит.
-бит.
Эллиптическая кривая широко используется для построения криптосистем []. Одним из инструментов построения генераторов псевдослучайных последовательностей является эллиптическая кривая над конечным полем.
Эллиптическая кривая
![]() над простым полем
над простым полем
![]() ,
где
,
где
![]() ,
задается уравнением в форме Вейерштрасса
,
задается уравнением в форме Вейерштрасса
![]() ,
где
,
где
![]() .
.
Халлгрен в 1994 году в
работе [] рассмотрел датчик псевдослучайной последовательности,
который называется арифметической прогрессией на
![]() с начальным членом
с начальным членом
![]() и разностью
и разностью
![]() и задается следующим рекуррентным соотношением:
и задается следующим рекуррентным соотношением:
где за
![]() обозначена групповая операция в
обозначена групповая операция в
![]() .
.
Выходными значениями датчика (1) могут быть
либо точки
![]() ,
либо только их абсциссы
,
либо только их абсциссы
![]() ,
либо только их ординаты
,
либо только их ординаты
![]() .
.
Следует отметить также
статистическую безопасность генератора псевдослучайных чисел,
построенного на базе арифметической прогрессии на эллиптической
кривой. Она обладает хорошими статистическими свойствами, что
показано в работе []: равномерностью распределения элементов
арифметической прогрессии для большого
![]() ,
также указан порядок величины отклонения от равномерности
,
также указан порядок величины отклонения от равномерности
![]() .
.
Для случая, при котором
известна разность
![]() и старшие биты
и старшие биты
![]() и
и
![]() в работе [] Гутиэрехом и Ибиасом предложен эффективный алгоритм
нахождения
в работе [] Гутиэрехом и Ибиасом предложен эффективный алгоритм
нахождения
![]() для генераторов, построенных на базе арифметической прогрессий на
эллиптической кривой, следовательно, он не обладает криптографической
безопасностью. Значит, секретным ключом в генераторе псевдослучайных
чисел (1) должны являться
для генераторов, построенных на базе арифметической прогрессий на
эллиптической кривой, следовательно, он не обладает криптографической
безопасностью. Значит, секретным ключом в генераторе псевдослучайных
чисел (1) должны являться
![]() и
и
![]() .
В этом случае не известны эффективные алгоритмы предсказания бит, и
генератор (1) является криптографически безопасным.
.
В этом случае не известны эффективные алгоритмы предсказания бит, и
генератор (1) является криптографически безопасным.
В работе [] в более общем виде рассмотрены
генераторы псевдослучайных последовательностей типа арифметическая
прогрессия на эллиптической кривой. Пусть порядок
![]() группы
группы
![]() равен
равен
![]() .
.
Последовательность
![]() точек
точек
![]() ,
удовлетворяющих рекуррентному соотношению:
,
удовлетворяющих рекуррентному соотношению:
называют
![]() -последовательностью
порядка
-последовательностью
порядка
![]() ,
а
,
а
![]() – характеристическим многочленом над
– характеристическим многочленом над
![]() .
.
-
Используя обозначения
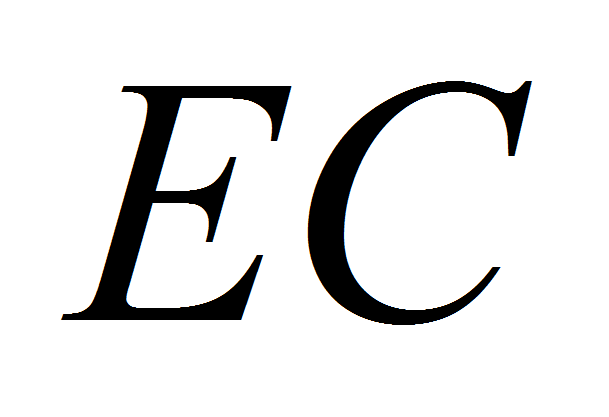 -последовательностей,
последовательность, заданная формулой (1), называется
-последовательностей,
последовательность, заданная формулой (1), называется
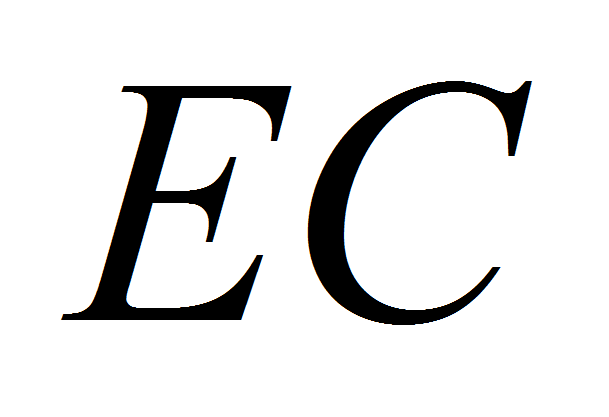 -последовательностью
первого порядка и характеристическим многочленом
-последовательностью
первого порядка и характеристическим многочленом
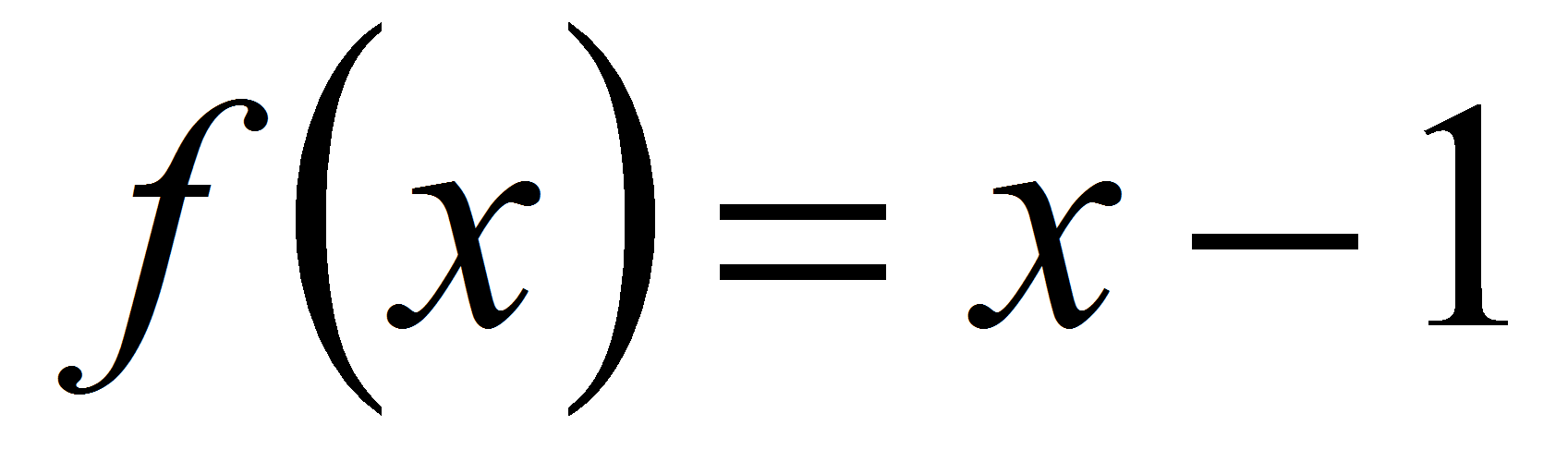 .
.
О последовательности,
заданной формулой (2), известно, что период
![]() –последовательности
(2) есть делитель периода ее характеристического многочлена []. В
работе [] показано,
что наибольший период имеет примитивный многочлен над полем
–последовательности
(2) есть делитель периода ее характеристического многочлена []. В
работе [] показано,
что наибольший период имеет примитивный многочлен над полем![]() .
.
Найдем примитивные многочлены второй степени, для чего воспользуемся следующей теоремой.
Теорема 1.
([]).Нормированный многочлен
![]() ,
степени
,
степени
![]() является примитивным многочленом над полем
является примитивным многочленом над полем
![]() в том и только в том случае, если
в том и только в том случае, если
![]() – примитивный элемент поля
– примитивный элемент поля
![]() и наименьшим натуральным числом
и наименьшим натуральным числом
![]() ,
для которого степень
,
для которого степень
![]() переменной
переменной
![]() сравнима по модулю
сравнима по модулю
![]() с некоторым элементом поля
с некоторым элементом поля
![]() ,
является
,
является
![]() .
.
Если
![]() – примитивный многочлен над
– примитивный многочлен над
![]() ,
то имеет место сравнение
,
то имеет место сравнение
![]() .
.
В работе [] доказано более сильное утверждения касающаяся многочленов второй степени:
Утверждение 1
[]. Если многочлен
![]() неприводим в
неприводим в
![]() ,
то
,
то
![]()
Следствие [].
Нормированный неприводимый многочлен
![]() ,
где
,
где
![]() и
и
![]() – простое число Мерсенна, является примитивным многочленом над
полем
– простое число Мерсенна, является примитивным многочленом над
полем
![]() в том и только в том случае, если
в том и только в том случае, если
![]() – образующий элемент в
– образующий элемент в
![]() .
.
Из следствия к утверждению можно сделать
вывод, что при использовании чисел Мерсенна, можно построить
генератор псевдослучайных чисел на базе
![]() последовательностей второго порядка с периодом
последовательностей второго порядка с периодом
![]() не проверяя многочлен на примитивность, а проверить только
не проверяя многочлен на примитивность, а проверить только
![]() – образующий элемент в
– образующий элемент в
![]() .
.
Разработка генератора псевдослучайных чисел на точках эллиптической кривой с использованием квадратичных полей Галуа.
-
Рассмотрим другую схему предложенную в
работе [], когда меняются коэффициенты, а точки остаются
фиксированными.
 для вычисления коэффициентов будем использовать поля Галуа,
построенные по неприводимому многочлену
для вычисления коэффициентов будем использовать поля Галуа,
построенные по неприводимому многочлену
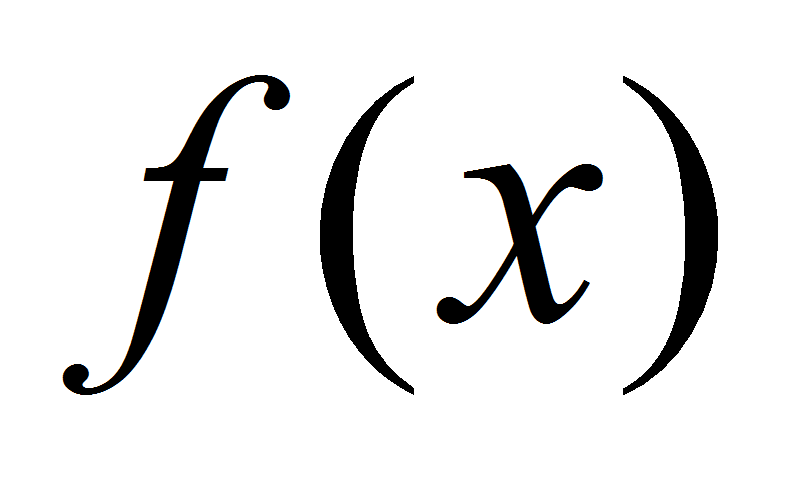 степени
степени
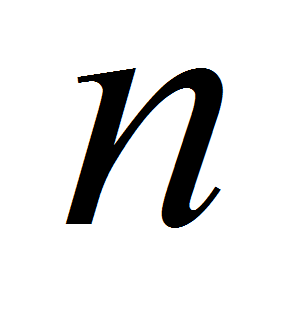 ,
где
,
где
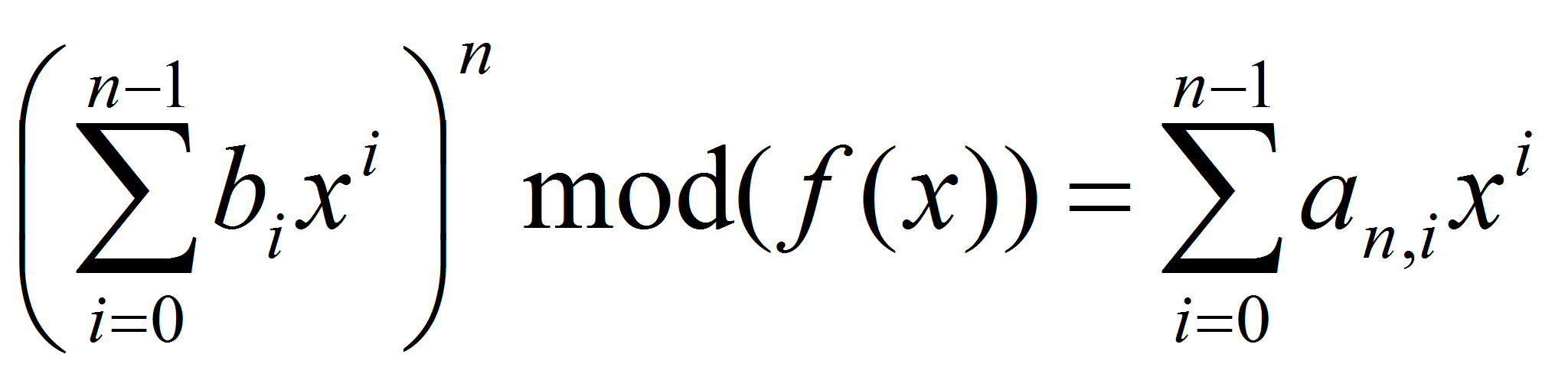 .
. -
Докажем ряд утверждений для исследования
на длину периода последовательности псевдослучайных чисел
построенной с помощью квадратичных полей Галуа, то есть
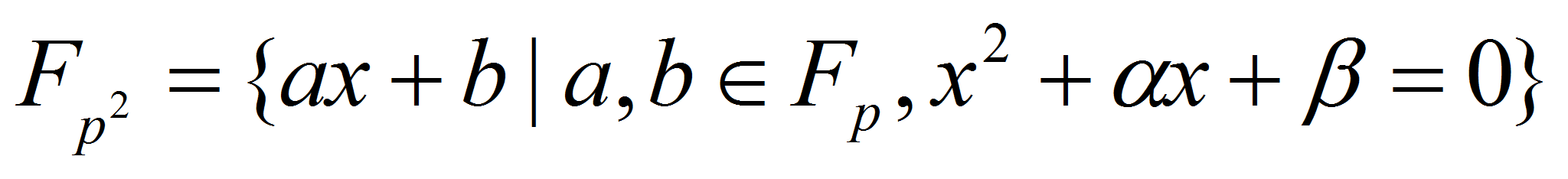 ,
где
,
где
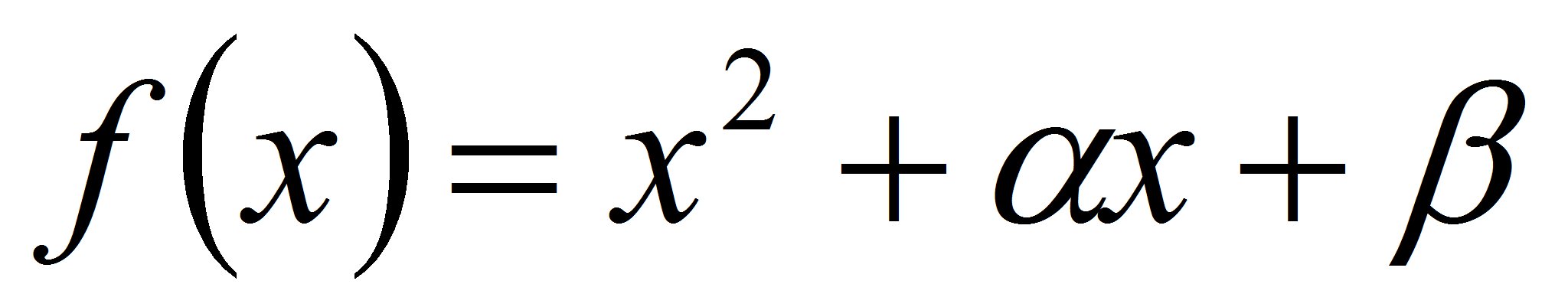 - неприводимый многочлен над
- неприводимый многочлен над
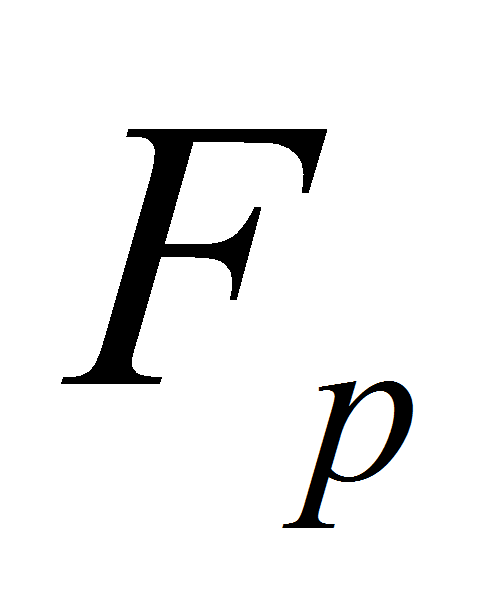 и двучлена
и двучлена
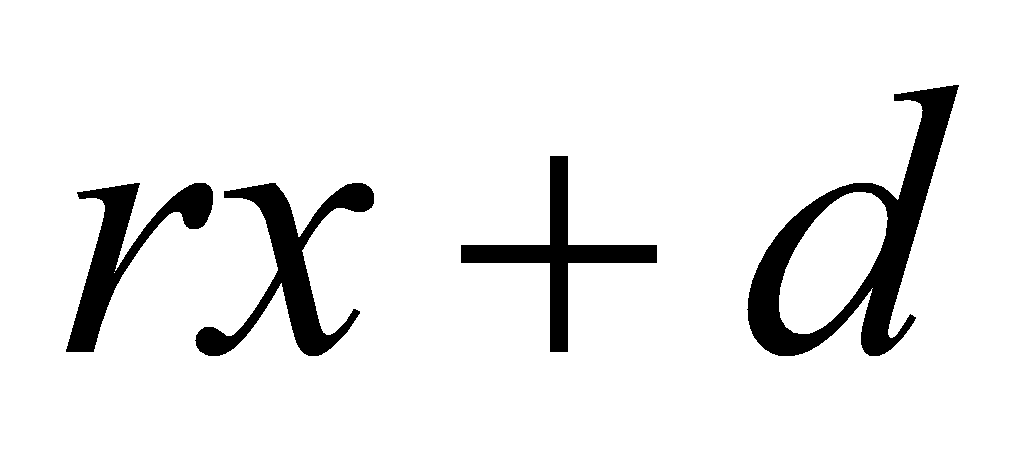 являющегося образующим элементам в
являющегося образующим элементам в
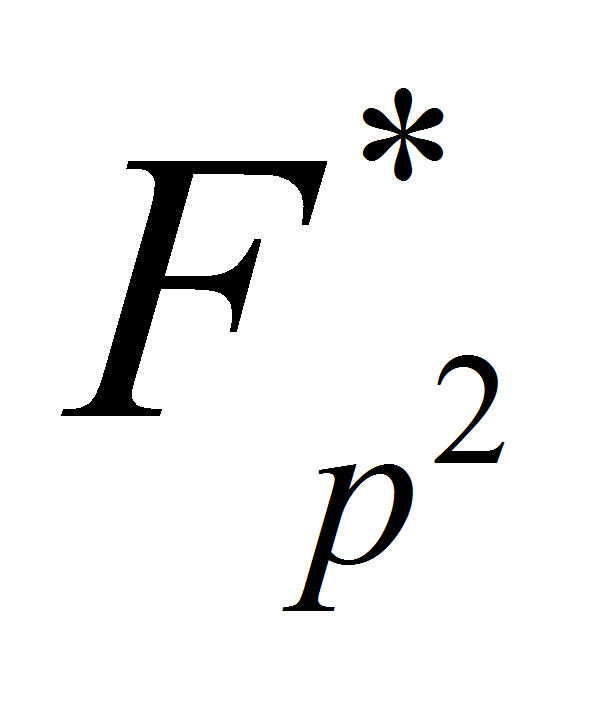 .
. -
Утверждение 2.
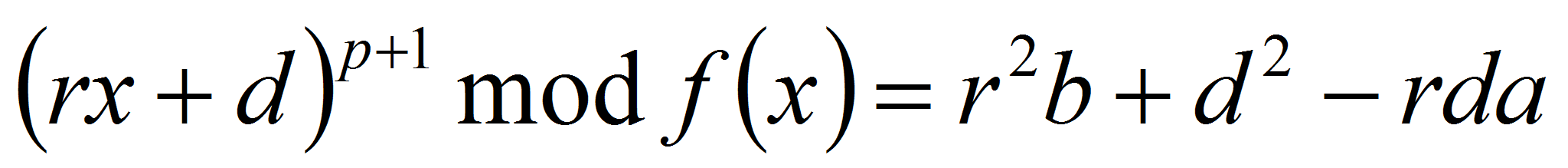 ,
где
,
где
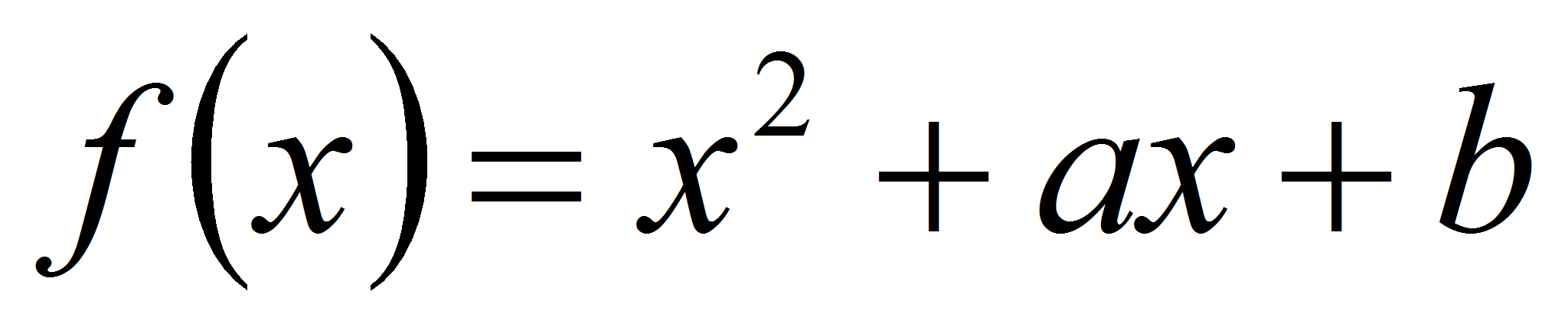 - неприводимый многочлен над
- неприводимый многочлен над
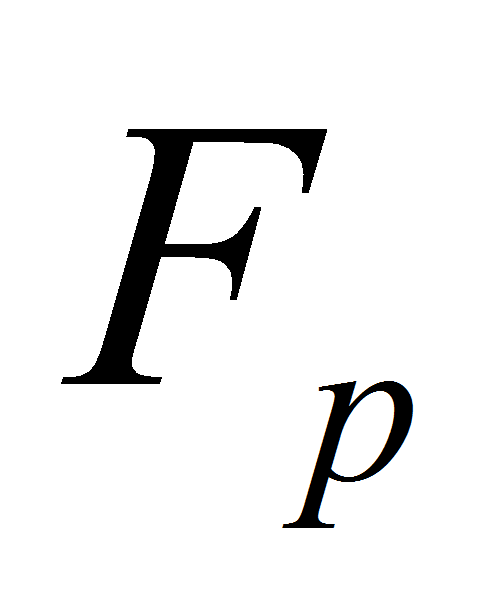 .
. - Доказательство
-
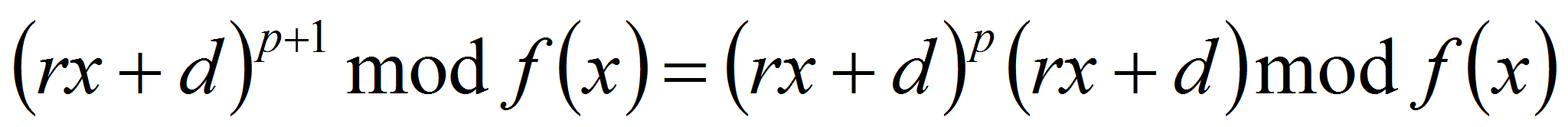
-
Так как поле
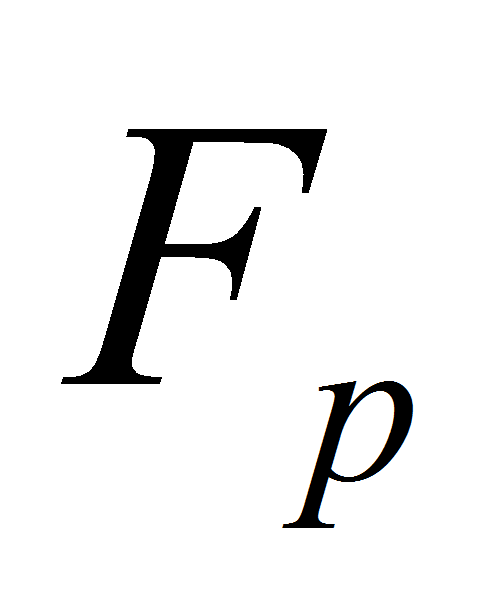 характеристики
характеристики
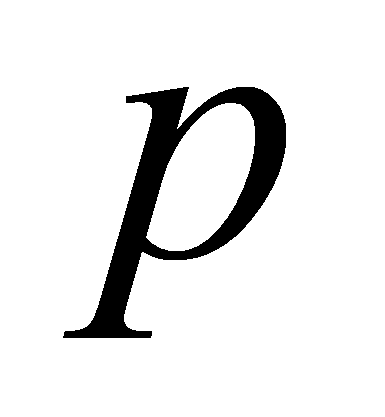 ,
то
,
то
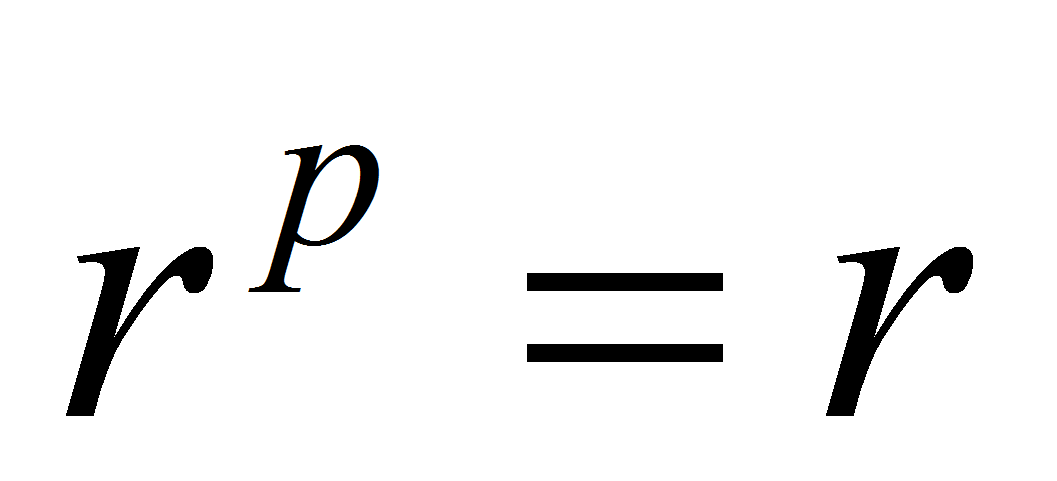 ,
,
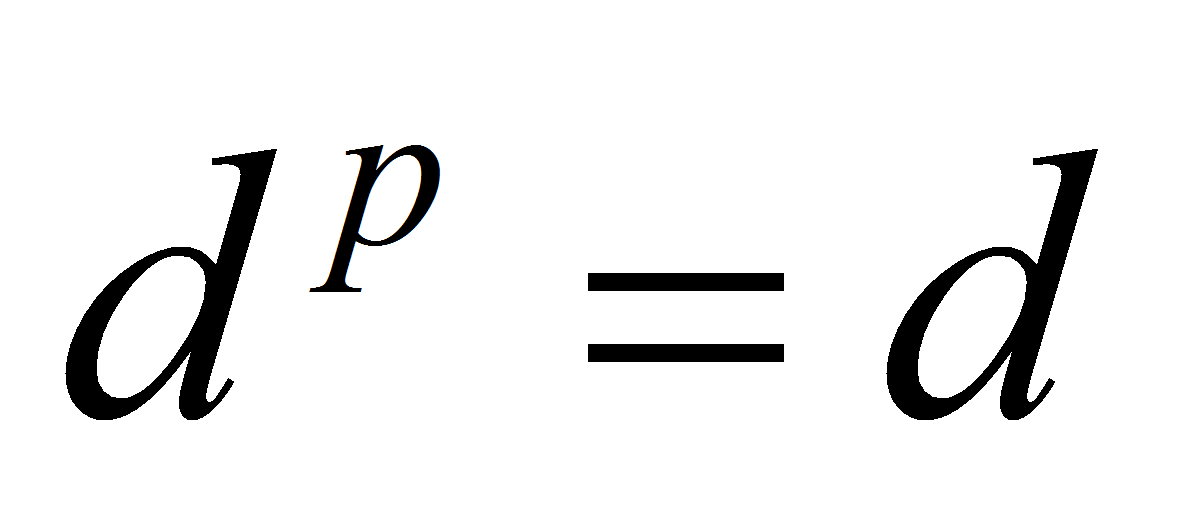 следовательно
следовательно
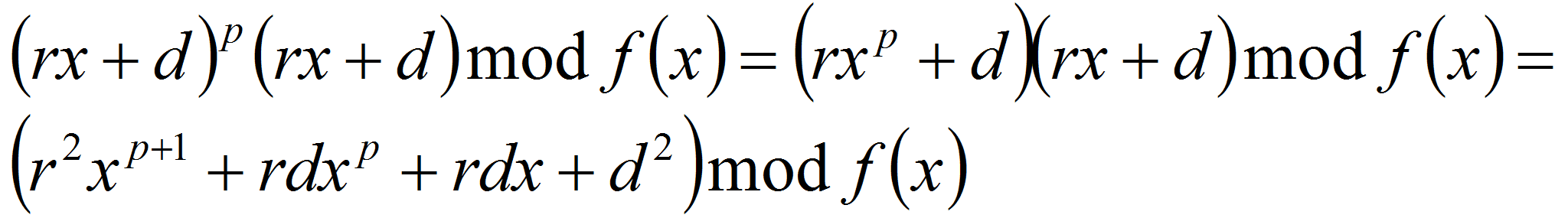
-
Из утверждения 1 следует, что
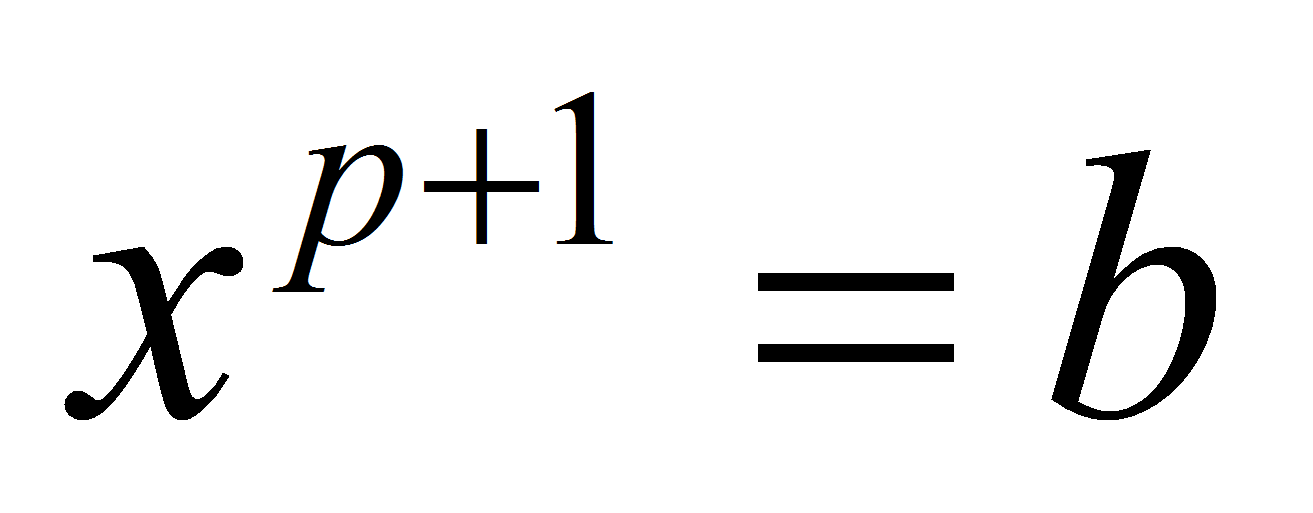 ,
а
,
а
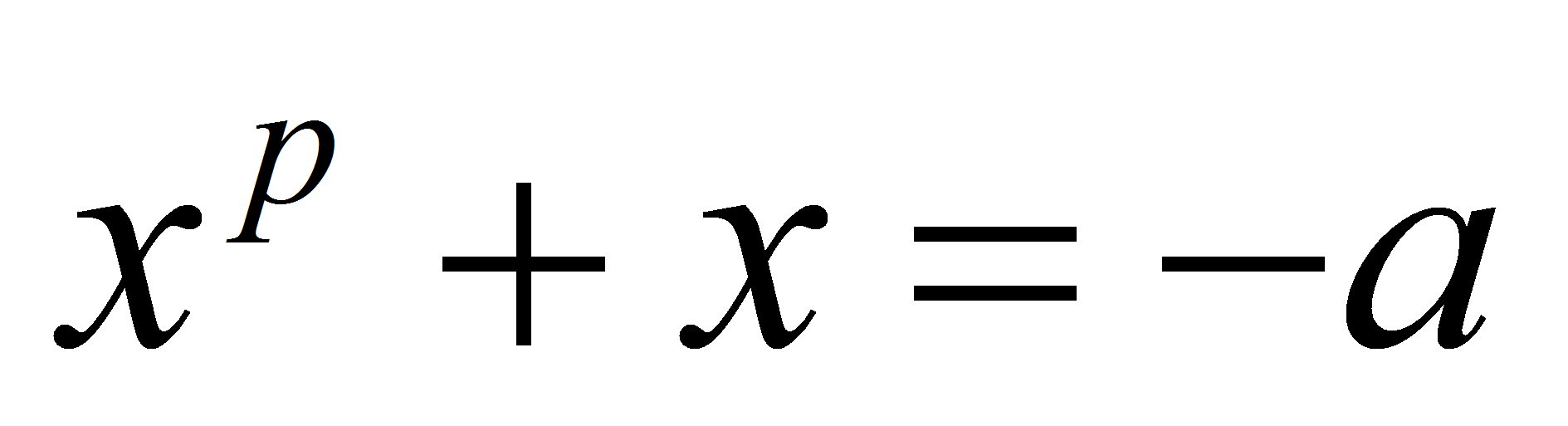 ,
то
,
то
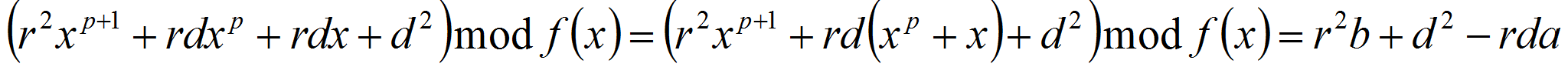
- Утверждение доказано.
-
Из утверждения 2 следует критерий выбора
двучлена
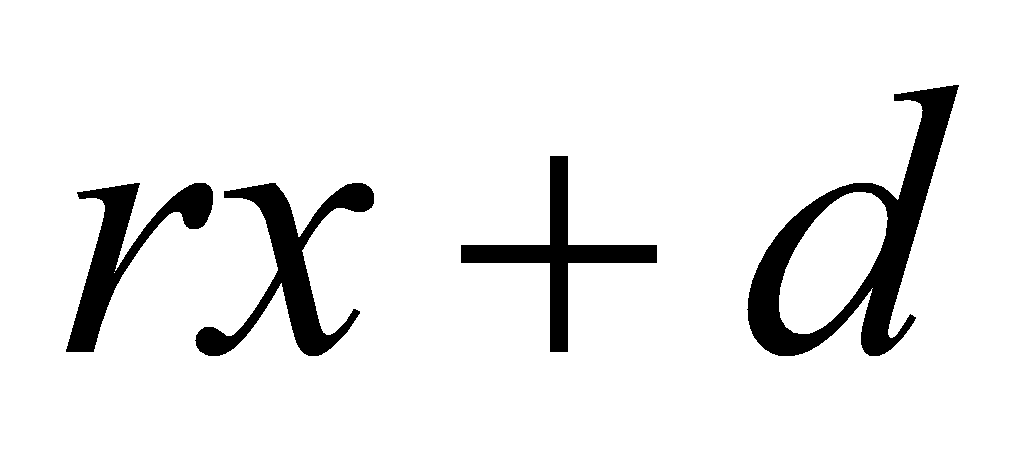 для построения последовательности.
для построения последовательности. -
Критерий 1.
Двучлен
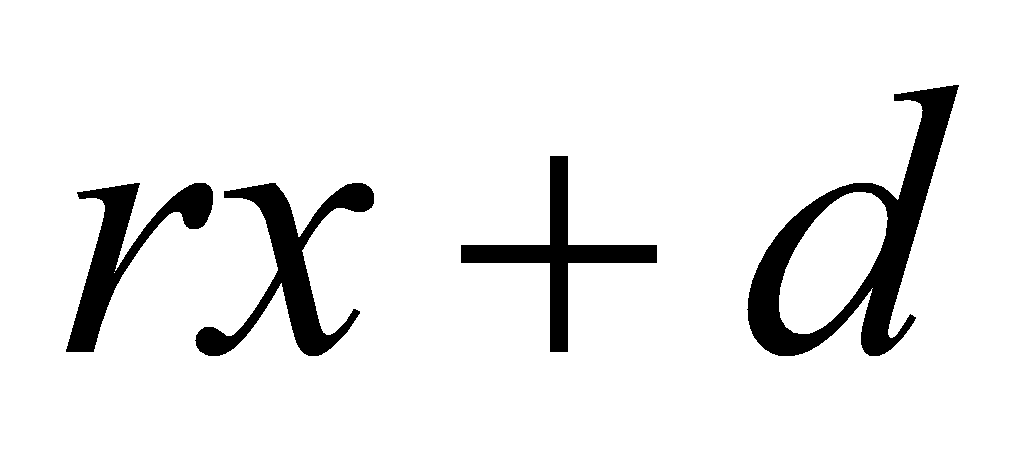 будет образующим элементом в
будет образующим элементом в
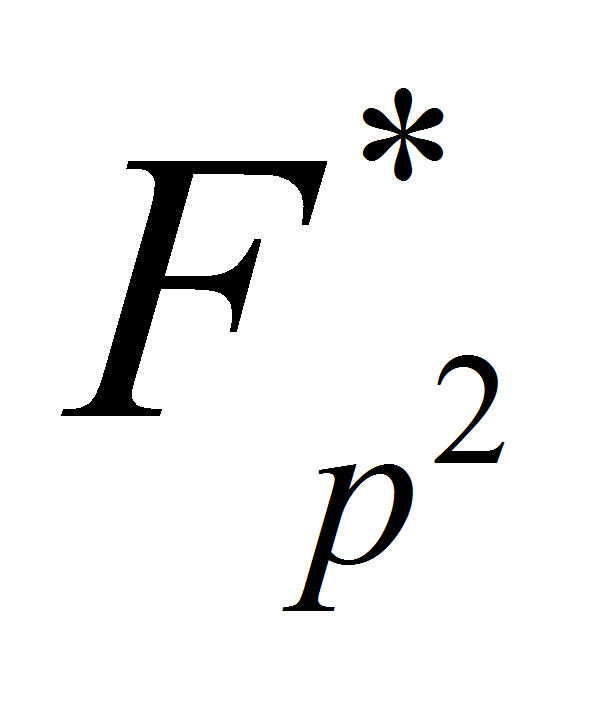 ,
только если
,
только если
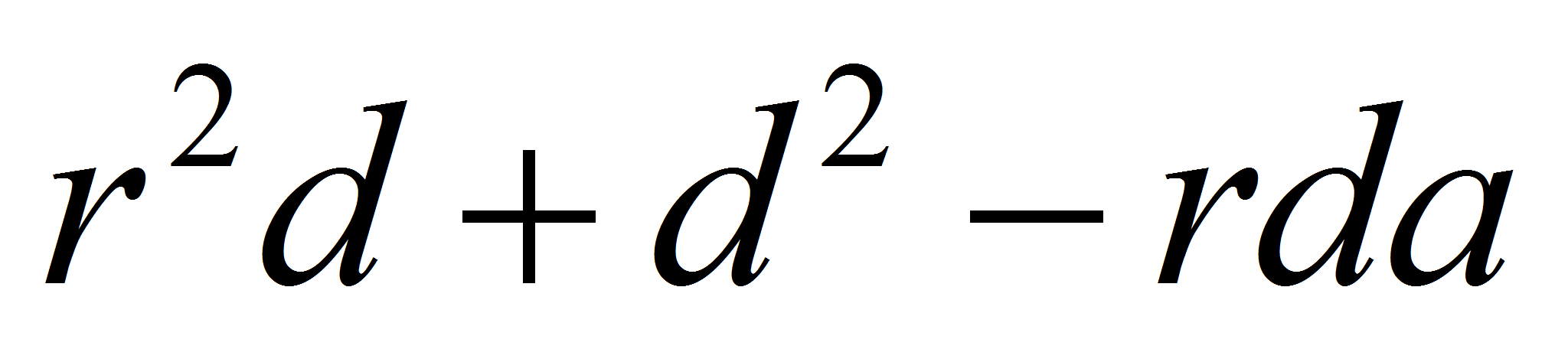 - образующий элемент в
- образующий элемент в
 .
. - Выводы
-
В статье проведен анализ
ЕС-последовательностей, особенно уделено внимание
последовательностям второго порядка. Доказано утверждение, которое
позволяет выработать критерий, которому должно удовлетворять
последовательность точек эллиптической кривой, полученная с помощью
квадратичных полей Галуа, которая могла бы иметь максимальный
период, равный
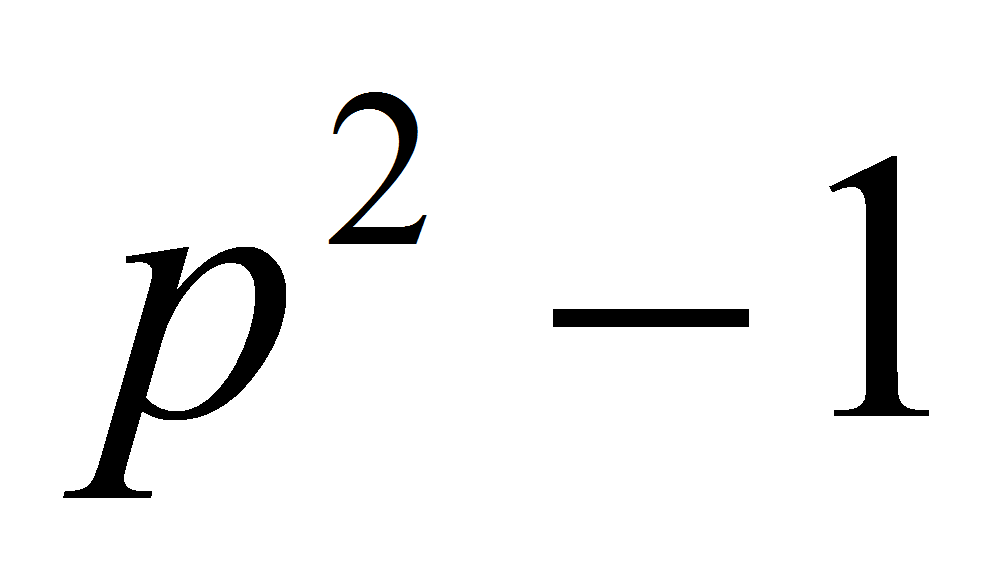 .
При условии, что
.
При условии, что
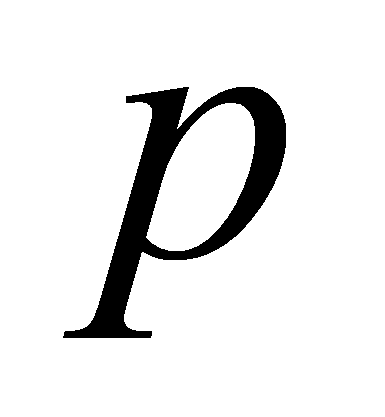 большое простое число,
большое простое число,
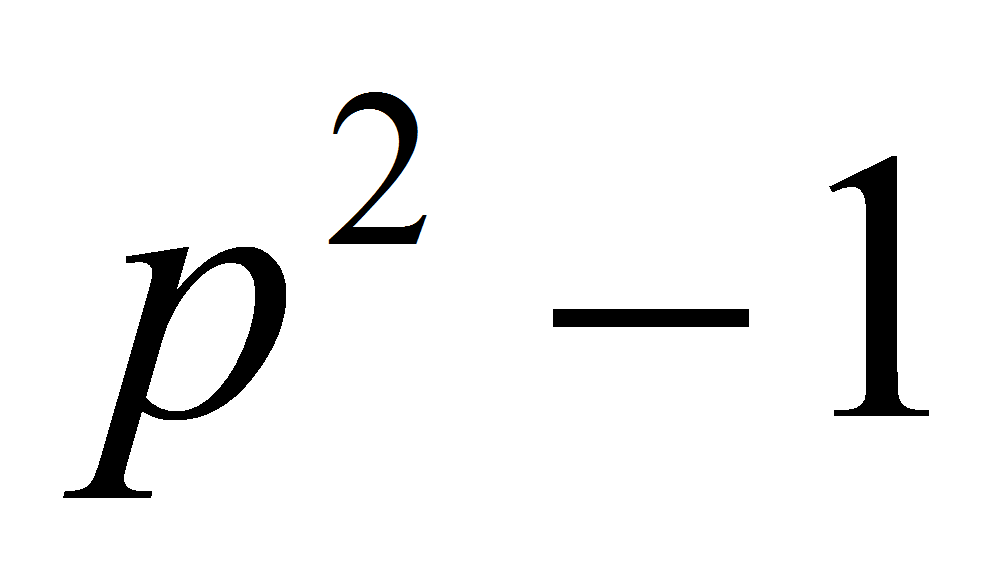 - большое число. Следовательно, при большом
- большое число. Следовательно, при большом
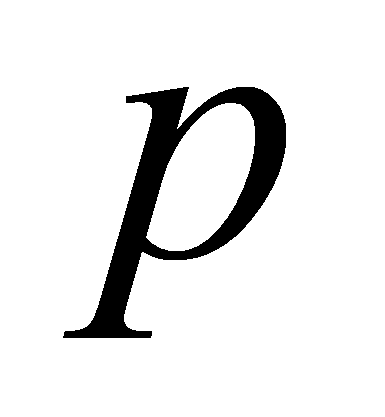 ,
построенная последовательность будем иметь большой период.
,
построенная последовательность будем иметь большой период. -
- Литература:
- Бабенко М.Г. О выборе коэффициентов для некоторых ЕС-последовательностей порядка 2// Вестник поморского университета. Серия Естественные науки, г. Архангельск, №2, 2010, – С 76-80
- Лидл Р., Нидеррайтер Г. Конечные поля: Пер. с англ. В 2 – х т.: Т.1. М., Мир, 1988.
- Рябко Б. Я., Фионов А. Н. Криптографические методы защиты информации: Учебное пособие для вузов. – М.: Горячая линия–Телеком, 2005. – 229 с.
- Червяков Н.И., Бабенко М.Г. Системы защиты данных на эллиптической кривой. Модулярная арифметика. – M.: LAMBER. – 2011. – 119 c.
- Gong G., Lam C. Linear recursive sequences over elliptic curves. – In: Sequences and their applications. – London: Springer, 2002, P. 182 – 196.
- Gutierrez J. and Ibeas A. Inferring sequences produced by a linear congruential generator on elliptic curves missing high-order bits // Designs, Codes and Cryptography, 41, 2007, P. 199-212.
- Hallgren S. Linear congruential generators over elliptic curve. // Cornegie Mellon Univ., 1994, CS-94-M3, P. 1-10.
- Koblitz N. Elliptic curve cryptosystems // Mathematics of Computation, 1987. Vol. 48. No. 177, P. 203-209.
- Nahassni E.E., Shparlinski I. On the uniformity of distribution of congruential generators over elliptic curves. // In: Sequences and their applications. – London: Springer, 2002, P. 257-261.

