В статье приводится описание метода вычисления актуарной приведенной стоимости кредита. Алгоритм базируется на построении дерева решений, а также оценке параметров функции интенсивности отказов в выплатах.
Ключевые слова: страхование, кредитные риски, рейтинг неплатежеспособности, дерево решений.
Потребительские виды кредита являются наиболее доходными видами кредитов, выдаваемыми банками. Но именно они имеют очень большую степень кредитного риска.
Алгоритм позволяет определять вес каждого фактора в итоговой оценке в соответствии с его влиянием, выявленным статистическими методами. Для этого необходимо выставлять рейтинговый балл [1] на этапе выдачи кредита и сопоставлять его с баллом рейтинговой группы, для которой заранее задана вероятность неплатежеспособности. Факторами могут выступать такие показатели как: возраст, пол, образование, сумма кредита, срок кредита, уровень дохода, семейное положение, первый или повторный кредит, цель кредитования и др. Выбор факторов обусловлен тем, что их можно легко проверить по заполняемой анкете на выдачу кредита.
Вероятность банкротства физического лица, обладающего определенными признаками, вычисляется так:
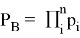
где
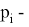
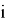
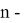
Рейтинговый балл можно вычислить следующим образом:
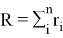
где
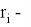
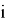
Однозначная связь между рейтинговым баллом и вероятностью банкротства:
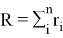
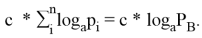
где
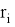
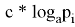
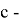
Сопоставим рейтинг заемщика рейтинговой группе, которая характеризуется вероятностью банкротства. Таким образом, все физические лица разместятся по группам, которым однозначно сопоставится максимальная вероятность разорения.
Рассмотрим способ выбора значимых некоррелированных признаков с помощью дерева решений, которое состоит из ребер и узлов. Дерево решений позволяет выделить наиболее значимые признаки с точки зрения увеличения количества информации. Будем применять формулу для вычисления энтропии. Рассмотрим множество
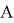
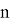
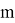
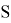
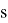
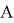
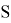
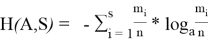
Атрибут будем выбирать таким образом, чтобы после классификации энтропия относительно целевой функции стала как можно меньше. Далее рассчитаем прирост информации. Пусть множество
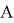
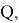
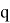
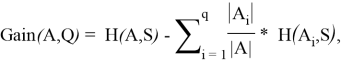
где
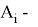
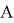
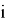
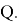
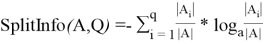
Для выбора подходящего атрибута будем использовать следующий критерий, как максимизацию значения
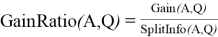
При построении дерева решений на каждом этапе происходит процедура расчета прироста информации, благодаря этому осуществляется упорядочивание признаков по влиянию на целевую функцию. В ходе расчета корреляции атрибутов легко исключаются коррелированные признаки исходя из наименьшего влияния на целевую функцию. Поэтому при расчете рейтинга участвуют только те некоррелированные или слабо коррелированные признаки, которые оказывают влияние на вероятность дефолта.
После определения рейтинга заемщика и подбора для него подходящей рейтинговой группы необходимо определить параметры функции интенсивности для расчета страховой премии. Будем использовать функцию интенсивности Мейкхема, так как постоянное слагаемое
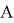
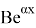
Будем проводить оценку параметров модели следующим образом [2]. Составим систему из трех уравнений с тремя неизвестными
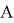
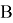
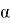
- Рассмотрим функцию распределения модели Мейкхема:
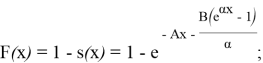
- Найдем нижний
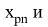
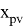
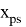
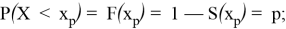
- Тогда система нелинейных уравнений будет иметь вид
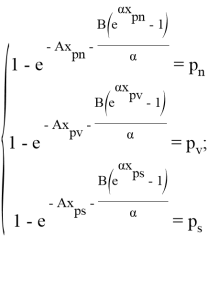
- Решив систему, мы получим оценки параметров
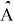
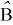
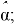
- Оцененная функция интенсивности будет иметь вид
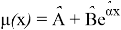
- Таким образом, получим формулу для стоимости страхования [3]
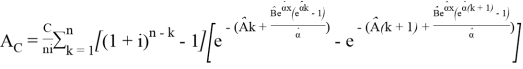
В случае, когда выплаты происходят непрерывно
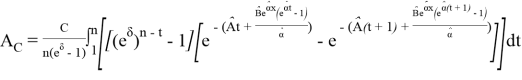
Литература:
- Петухова М. В. Рейтинговая методика оценки кредитного риска физических лиц. — Новосибирск.: Вестник НГУ. Серия: Социально-экономические науки. 2011. Т. 11, вып. 3, с.86–93.
- Леонова О. В. Моделирование смертности населения с помощью аналитических законов на примере России. — Иркутск.: Известия Байкальского государственного университета. 2019. Т. 29, вып. 1, с. 95–106.
-
Беляевских Е. А. Исследование и анализ кредитных рисков методами актуарной математики: дис.... канд. экон. наук: — М.: МГУ им. М. В. Ломоносова, 2013.


