В статье авторы доказывают теорему косинусов для четырехугольников в терминах рациональной тригонометрии.
Ключевые слова: рациональная тригонометрия, квадрация, апертура, теорема косинусов.
Новая форма тригонометрии, рассматриваемая в данной работе, называется рациональной тригонометрией. Основные понятия и законы рациональной тригонометрии для евклидовой геометрии впервые сформулированы в 2005 г. Н.Дж. Уайлдбергером [1].
Суть новой тригонометрии заключается в переопределении тригонометрических соотношений без использования тригонометрических функций с помощью введения вместо традиционных расстояний и углов таких понятий, как квадрация (quadrance) и апертура (spread). Данный подход позволяет отказаться от использования тригонометрических таблиц и, как следствие, приближенных вычислений, т. е. он зачастую оказывается более точным.
Законы рациональной тригонометрии заменяют теоремы косинусов, синусов и десятки других тригонометрических формул. Наиболее важными новыми законами являются тройная формула для квадрации, закон апертур, закон пересечений и тройная формула для апертур. Теорема Пифагора, переформулированная в терминах рациональной тригонометрии, также играет ключевую роль. Вывод этих законов прост, для освоения требуется знание базовой алгебры школьного уровня.
Несмотря на то, что идеи рациональной тригонометрии вызвали неоднозначное впечатление у математического сообщества, ее методы нашли применение в решении теоретических и практических задач геометрии, комбинаторики, робототехники.
Рациональная тригонометрия решает многие практические проблемы проще и элегантнее, чем классическая тригонометрия, и часто заканчивается ответами, которые наглядно более точны. На самом деле рациональная тригонометрия настолько элементарна, что почти все вычисления могут быть выполнены вручную. Таблицы или калькуляторы не нужны, хотя последние, безусловно, ускоряют вычисления.
Рассмотрим основные понятия рациональной тригонометрии – квадрации сторон треугольника:
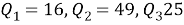
и апертуры внутренних углов:
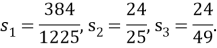
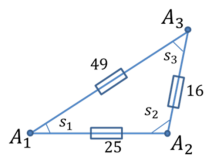
Рис. 1.
Объясним значение этих терминов и покажем, как эти числа были получены.
Квадрация — это квадрат расстояния между двумя точками. Если расстояние
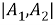
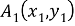
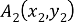
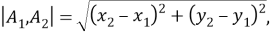
то квадрация между точками
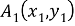
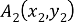
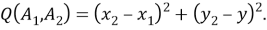
С этой точки зрения квадрация является более фундаментальной величиной, поскольку он не включает функцию квадратного корня. На рисунке 1 маленькие прямоугольники вдоль сторон треугольника указывают на то, что измеряется квадрация, а не расстояние.
Апертура измеряет «разделение» двух пересекающихся прямых, т. е. насколько «далеко разбросаны» прямые друг от друга. Исторически существует ряд решений этой проблемы.

Рис. 2.
Наиболее знакомым является нахождение угла между прямыми (или нахождение разделения двух линий). Есть разные подходы к вопросу о том, как измерить разделение двух линий. Один из них является определение апертуры угла между прямыми. Возьмем любую точку
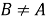
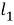
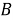
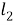
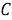
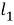
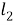
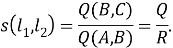
Число
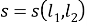
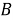
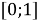
Вычислим апертуры внутренних углов треугольника
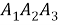
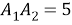

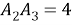
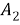
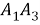
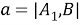
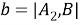
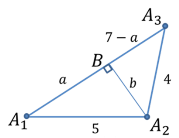
Рис. 3.
Применяя теорему Пифагора для прямоугольных треугольников
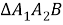
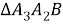
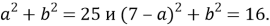
Решая систему, состоящую из этих двух уравнений, получаем, что:
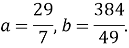
Далее получаем:
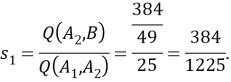
Аналогично находим, что:
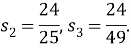
Справедливы следующие законы рациональной тригонометрии.
1. Тройная формула для квадрации. Три точки коллинеарны тогда и только тогда, когда
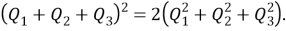
2.
Теорема Пифагора.
Треугольник
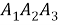
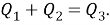
3.
Закон апертуры.
Для любого треугольника
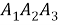
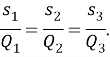
4.
Закон пересечений.
Для любого треугольника
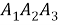
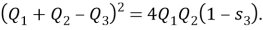
5.
Тройная формула апертур.
Для любого треугольника
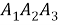
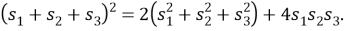
Эти формулы связаны интересным образом, и их вывод достаточно прост. Существует также множество альтернативных формулировок этих законов, а также обобщений для четырех квадраций и апертур, которые становятся важными при изучении четырехугольников.
Сформулируем и докажем теорему косинусов для четырехугольника [2–4] в терминах рациональной тригонометрии.
Рассмотрим четырехугольник
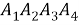
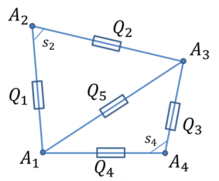
Рис. 4.
Пусть
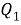
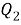
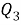
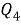
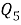
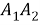
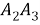
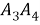
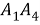
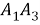
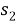
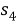
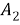
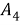
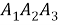
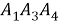
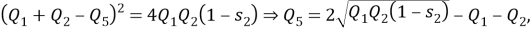

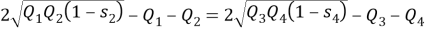
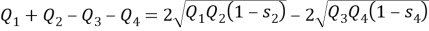
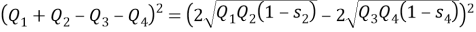
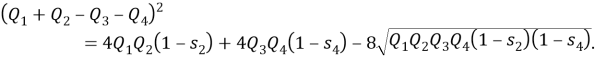
Полученное соотношение между квадрациями сторон четырехугольника назовем теоремой косинусов для четырехугольника в терминах рациональной тригонометрии.
Литература:
1. Wildberger N. J. Divine Proportions: Rational Trigonometry to Universal Geometry. — Sydney, 2005
2. Коксетер Г. С. М., Грейтцер С. П. Новые встречи с геометрией. М., 1978. (Серия Библиотека математического кружка)
3. Ceргeeв И. Н. Примeни мaтeмaтику. / Ceргeeв И. Н., Oлexник C. Н., Гaшкoв C. Б. — Мocквa: Нaукa, 1989 — C. 240
4. Шыныбeкoв A. Н. Гeoмeтрия: учeбник для 9 клacca oбщeoбрaзoвaтeльныx шкoл. / Шыныбeкoв A. Н. — Aлмaты: Aтaмурa, 2005. — C. 224

