Разделение угла на равные части



В статье решается задача деления угла на n равных частей, которая не решена до сих пор в общем виде.

Ключевые слова: угол, биссектриса, деление угла, хорда, дуга, параллельность прямых, окружность.

Отсутствие алгебраического решения задачи не означает, что она не имеет геометрического решения. Мною исследована задача деления угла на необходимое количества равных частей, и найдено ее замечательное решение.

Анализ

Любые равные части можно изобразить на числовой прямой, выбрав единичный отрезок. Если угол разделен на равные части, то можно ли его изобразить на числовой прямой? Да, можно. Для этого нужно найти единицу измерения деления на равные части. Попытаемся найти единицу измерения.

Пусть заданный угол разделен на 2 и 4 равные части с хордой длиной 3 равные части с хордой расположен между равными частями 2 и 4. Тогда он на каком расстоянии расположен? Пусть он расположен на расстоянии от частей 4 и на расстоянии

от частей 2:

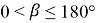
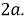
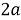
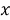
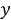
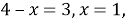
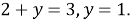
Значит, 3 равные части расположены между ними, следовательно, угол можно разделить на равные части (рис. 1).

Шаг 1. Проведем биссектрису угла

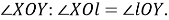
Шаг 2. Проведем биссектрису угла

и прямые Обозначим

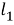
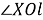
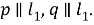
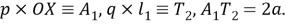
Шаг 3. Проведем дугу окружности Обозначим

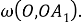
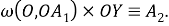
Шаг 4. Угол разделен на 2 равные части.

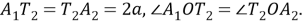
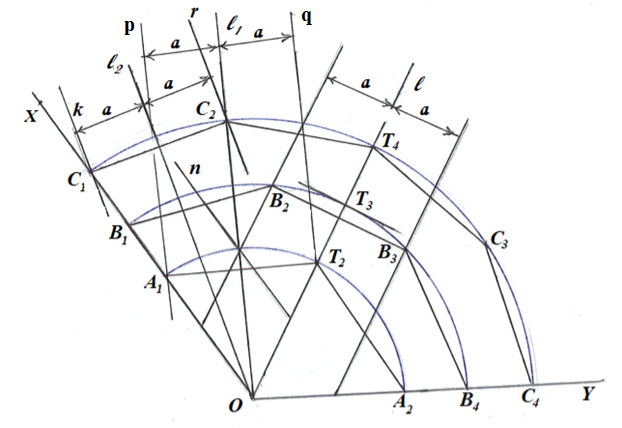
Рис. 1

Шаг 5. Проведем биссектрису угла и прямые

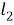
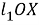
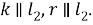
Шаг 6. Обозначим

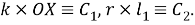
Шаг 7.

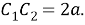
Шаг 8. Проведем дугу окружности Получившуюся дугу измеряем хордой

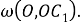
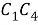
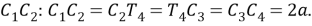
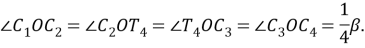
Шаг 9. Поскольку 3 равные части лежит на одинаковом расстоянии от равных частей 2 и 4, то отрезок делим пополам и обозначим через

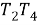
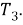
Шаг 10. Проведем дугу окружности

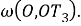
Шаг 11. Получившуюся дугу измеряем хордой

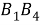
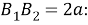
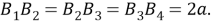
Шаг 12.

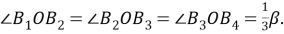
Отрезок принимаем за единицу измерения разделения угла на равные части. Хорду принимаем за единицу измерения дуги. Изложенным способом можно разделить угол на равных частей.

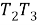
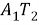
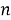
Построение

Применяя вышеизложенный способ, покажем разделение угла на 5 равных частей (рис. 2).

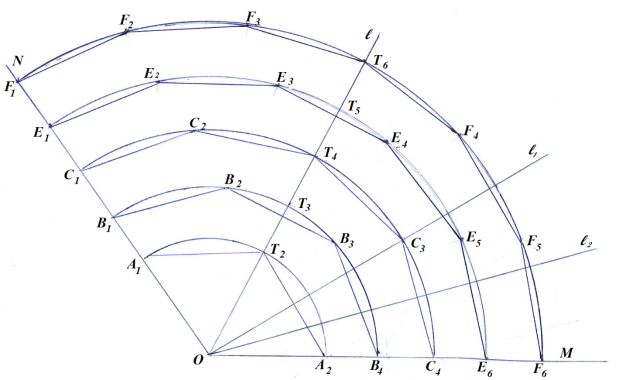
Рис. 2

Шаг 1. 5 равная часть лежит между равными частями 4 и 6.

Шаг 2. Начиная с точки строим точку удовлетворяющую равенству

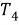
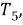
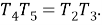
Шаг 3. Проведем дугу окружности Обозначим

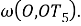
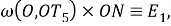
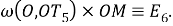
Шаг 4. Измеряем дугу хордой Тогда

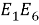
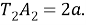
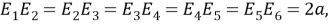
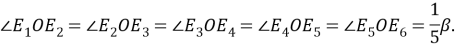
Продолжая таким образом, можно разделить угол на равных частей.

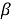
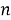
Доказательство

1. Построение для верно.
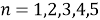
2. Будем предполагать, что построение верно для
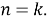
3. Докажем, что построение верно для Если построение верно для то оно будет верно для Но так как то построение верно и для

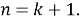
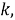
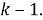
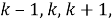
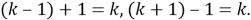
Деление угла на 1,5 равные части

1,5 равные части лежат между равными частями 2 и 1. Угол хорда которого равна отдельный угол. Угол хорда которого равна состоит из двух частей.

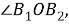
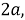
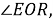
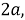
Шаг 1.

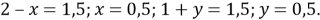
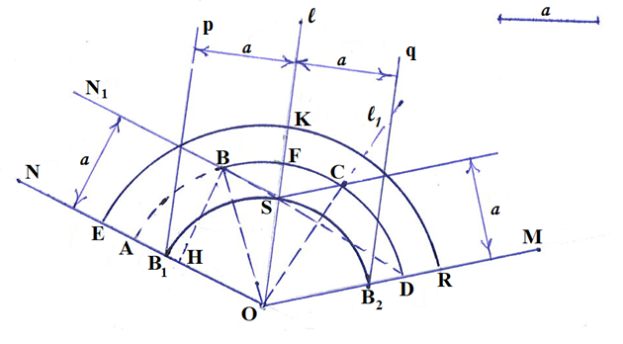
Рис. 3

Шаг 2. 1,5 равная часть равноотстоит от равных частей 2 и 1.

Шаг 3. Расстояние делим пополам и обозначим через

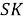
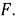
Шаг 4. Проводим дугу окружности Эта дуга пересекает сторону в точке а сторону в точке Измеряем дугу

хордой

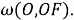
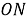
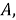
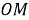
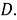
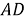
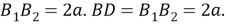
Шаг 5. Угол делим пополам.

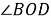
Шаг 6.

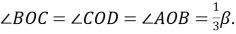
Этим способом угол можно разделить на части

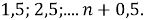
Исследование

Для применения изложенного способа к углам сперва данный угол разделить пополам, затем применить этот способ. Потом, объединяя по два, делится на

равных частей.

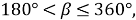
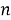
Литература:

1. Адлер А. Теория геометрических построений. Л.: Государственное учебно-педагогическое издательство. 1940. — 232 с.
2. Аргунов Б. И., Балк М. Б. Элементарная геометрия. М.: Просвещение. 1966. — 368 с.