Где материя, там геометрия.
Иоганн Кеплер
В работе рассматриваются формулы Мольвейде. В результате их исследования установлена тригонометрическая зависимость между длинами отрезков в точке пересечения биссектрис и значениями углов при вершинах некоторого треугольника. Полученные формулы можно использовать при решении задач в профильных классах по математике.
Ключевые слова: треугольник, биссектриса, длина, угол, синус, косинус.
Геометрия — удивительная наука. Её история насчитывает не одно тысячелетие, но каждая встреча с ней способна одарить и обогатить волнующей новизной маленького открытия, изумляющей радостью творчества. Действительно, любая задача элементарной геометрии является, по существу, теоремой, а ее решение — скромной математической победой.
Геометрия треугольника — одна из древнейших областей планиметрии. Наиболее активно развивалась в древней Греции и с середины 18–20 до середины 20-го века. В конце 20-го века развитие компьютеров дало возможность продолжать систематическое изучение геометрических структур, возникающих в треугольнике и их свойств. Наряду с этим, заметный прогресс в развитии данной области стал возможен благодаря экспериментальным исследованиям с использованием приближенных вычислений, подтвержденных методами вычислительной алгебры.
Давно известно, что изучение геометрии начинается с треугольника и в какой-то степени является основой геометрической науки. Также известно, что постоянно открываются его новые свойства.
Мольвейде Карл Брандан родился в Вальфенбютлерге, Германия 3 февраля 1774 года и умер 10 марта 1825 года. Немецкий математик и астроном в 1808 году опубликовал две формулы для решения косоугольных треугольников, получивших впоследствии его имя. До 1816 года работал в обсерватории Лейпцигского университета. В 1812 году он назначен ординарным профессором астрономии, а в 1814 году — ординарным профессором математики. С 1820 по 1823 годы был деканом философского факультета. Если а, в, с — длины сторон треугольника АВС , а А , В , С — величины его углов (рис.1), то
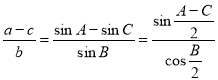
это равенство и аналогичные равенства, полученные перестановкой букв, называются формулами Мольвейде.
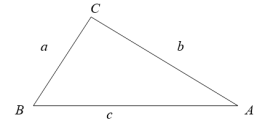
Рис. 1
Запишем эти формулы:
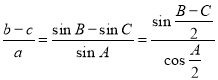
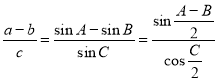
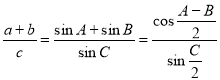
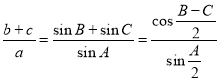
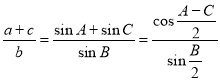
«Известно, что в треугольнике АВС биссектрисы АК , ВD и CM пересекаются в точке О (рис.2). Эта точка делит биссектрисы в отношении:
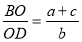
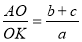
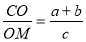
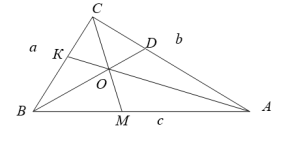
Рис. 2
Из выражений (6) и (7), можно записать:
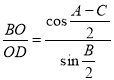
Из выражений (4) и (9), можно записать:
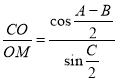
Из выражений (5) и (8) можно записать
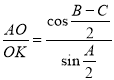
Полученные формулы (10), (11) и (12) — это тригонометрические зависимости, выражающие отношения между длинами отрезков биссектрис в точке их пересечения и значениями углов при вершинах некоторого треугольника.
Из треугольника АВС по теореме о биссектрисе внутреннего угла имеем:
для биссектрисы АК
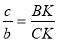
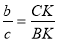
1) для биссектрисы BD
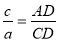
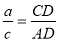
2) для биссектрисы CM
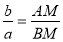
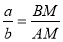
Используя выражения (14) и (15), получим:
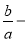
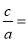
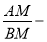
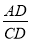
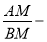
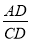
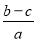
Используя выражения (16) и (2), имеем:
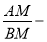
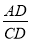
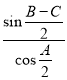
Используя выражения (13) и (14), получим:
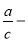
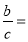
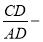
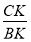
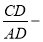
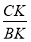
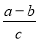
Используя выражения (18) и (3), имеем:
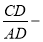
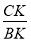
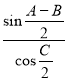
Используя выражения (13) и (15), получим:
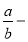
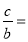
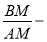
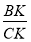
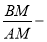
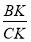
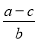
Используя выражения (1) и (20), имеем:
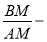
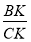
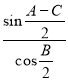
Полученные формулы (17), (19) и (21) это тригонометрические зависимости, выражающие разности отношений между длинами отрезков каждой стороны треугольника, на которые они разделены биссектрисами.
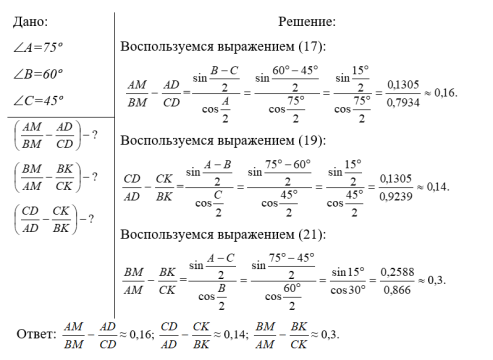
Задача. В треугольнике
АВС
известно, что
А=75º
,
В=60º
и
С=45º
. В треугольнике проведены биссектрисы
AK
,
BD
и
CM
, которые пересекаются в точке
O
(рис. 2). Найти следующие соотношения:
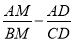
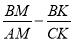
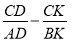
Литература:
- Выгодский М. Я. Справочник по элементарной математике. Москва. «Наука». 1986.
- Некрасов В. Б. Школьная математика. Издательство «Авалон». «Азбука — классика». Санкт–Петербург. 2006.

