Актуальность выбранной темы обусловлена необходимостью в школьном курсе математики уделять большее количество времени теме «Задачи с параметрами».
Ключевые слова: параметр, задачи с параметрами.
Выпускнику школы полезно владеть различными методами решения задач — аналитическими и графическими, уметь переводить словесное условие задачи в аналитическую форму — сводить ее к решению уравнений, неравенств и систем и совокупностей уравнений и неравенств. К сожалению, в программах по математике для неспециализированных школ задачам с параметром практически не отводится места, а, например, в учебнике для учащихся школ и классов с углубленным изучением курса математики («Алгебра и математический анализ для 10 и 11 классов», Н. Я. Виленкин, О. С. Ивашев-Мусатов, С. И. Шварцбурд) им отведено место только в 11-м классе.
Между тем, задачи с параметрами можно и нужно использовать уже начиная с линейных и квадратных уравнений и неравенств. Это могут быть задачи нахождения решений в общем виде, определения корней, удовлетворяющих каким-либо свойствам, исследования количества корней в зависимости от значений параметра. Так сделано в «Сборнике задач по алгебре для 8–9 классов», 1994 г. (авторы: М. Л. Галицкий, А. М. Гольдман, Л. И. Звавич). Важно, чтобы школьники уже на первых простых примерах усвоили: вопервых, необходимость аккуратного обращения с параметром — фиксированным, но неизвестным числом, поняли, что оно имеет двойственную природу. Во-вторых, что запись ответа существенно отличается от записи ответов аналогичных уравнений и неравенств без параметра.
Методически было бы правильно каждый пройденный тип уравнений и неравенств завершать задачами с использованием параметра. Во-первых, школьнику трудно привыкнуть к параметру за два-три занятия — нужно время. Во-вторых, использование подобных задач улучшает закрепление пройденного материала. В-третьих, оно способствует развитию его математической и логической культуры, а также развитию интереса к математике, поскольку открывает перед ним новые методы и возможности для самостоятельного поиска.
Ниже хотелось бы представить некоторые задачи с параметрами, которые в школьном курсе математики у учащихся вызывают трудности.
Задача 1:
Найти все значения, которые может принимать сумма x+a, если пара чисел (x, a) является решением неравенства
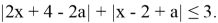
Решение:
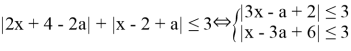
-
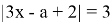
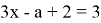
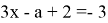
-
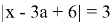
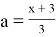
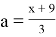
Наибольшее значение x+a равно 1,5+3,5=5.
Наименьшее значение x+a равно -1,5+0,5=-1.
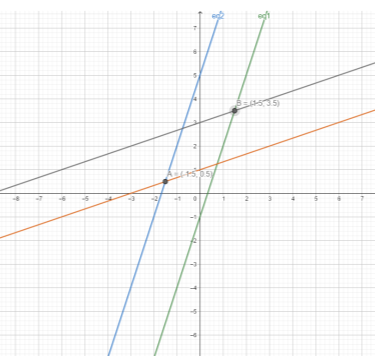
Ответ:
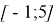
Задача 2:
При каких значениях параметра а уравнение
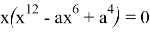
Решение:
Один из корней данного уравнения очевидно
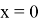
Пусть
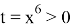
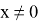
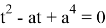
Данное квадратное уравнение будет иметь различные положительные корни, если выполняются условия:
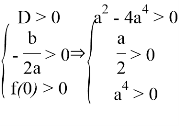
Решением данной системы является интервал
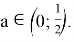
Исходное уравнение образует арифметическую прогрессию пятью корнями данного уравнения вида:
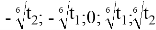
При условие, если
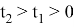
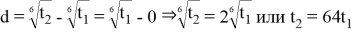
По теореме Виета из квадратного уравнения
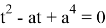
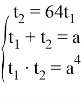
Решением этой системы будут числа
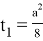
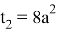
Подставляя эти значения во второе уравнение системы, получаем равенство
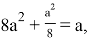
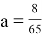
Ответ:
5 корней при
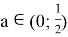
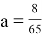
Задача 3:
Взависимости от значений параметра a решите неравенство
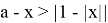
Решение:
Перепишем исходное неравенство в виде
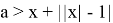
Рассмотрим две функции
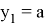
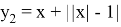
Вторую функцию, раскрывая модули,можно записать так:
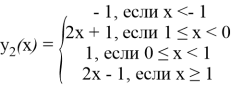
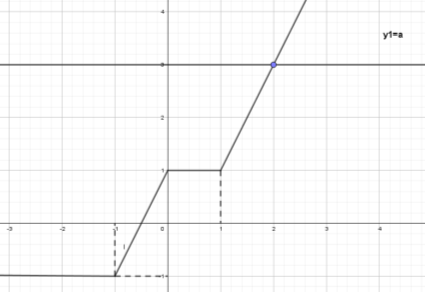
Графиком
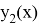
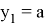
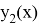
Из рисунка получаем:
При

При
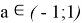
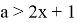
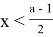
При
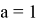
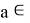
При

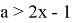
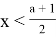
Ответ:
если

если
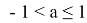
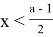
если

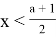
Задача 4:
Найдите все значения параметра t, при каждом из которых уравнение
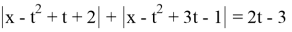
Решение:
Представим правую часть уравнения в виде
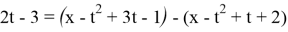
Сделаем замену
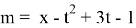
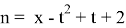
Тогда уравнение примет вид
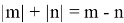
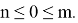
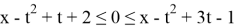
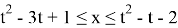
Уравнение имеет корни, ни один из которых не принадлежит интервалу (4; 19), за исключением, если правая граница отрезка решений не больше 4 или левая граница не меньше 19.
Получаем
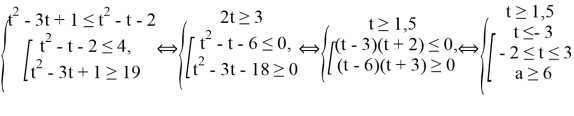
Ответ:
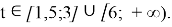
Задача 5: При каких a уравнение
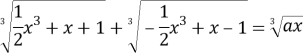
имеет ровно 4 корня?
Решение.
Заметим, что x=0 всегда будет корнем данного уравнения.
Поделим уравнение на
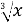
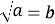
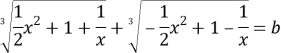
имело ровно три корня.
Исследуем для начала функцию
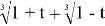
Функция четная.
Производная при t>0 будет
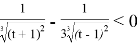
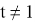
Следовательно, функция убывает на промежутке
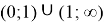
Очевидно, при больших t имеем
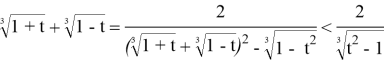
Поэтому
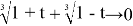
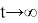
Итак, на положительной полуоси функция убывает и принимает все значения из промежутка
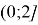
На отрицательной происходит то же самое из-за четности функции.
Обозначая за
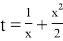
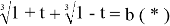
Уравнение (*) имеет единственный корень t=0 при b=2, имеет два корня (отличающихся знаком) при
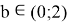
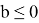
Пусть b=2.
Тогда необходимо чтобы t=0, то есть
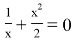
Пусть
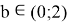
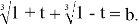
Нас интересует число корней уравнения
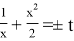
Выясним для этого, как устроена функция
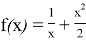
Производная этой функции
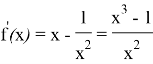
Значит,
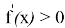
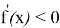
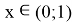
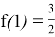

Будем считать, что t>0, тогда
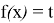
Это возможно только если этот корень x=1 и
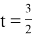
Итак,
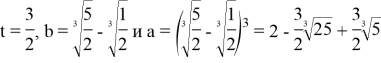
Ответ:
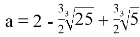
Литература:
- В. В. Локоть «Задачи с параметрами» / Издательство «Аркти» — 2005 г.
- А. И. Козко, В. Г. Чирский «Задачи с параметрами и другие сложные задачи» / Издательство «МЦНМО» — 2007 г.
- В. В. Мирошин Решение задач с параметрами. Теория и практика М.: Издательство «Экзамен», 2009г.







