О корнях кубического уравнения



Известно, что решение некоторых теоретических и практических задач, а также моделирование некоторых физических процессов требует определение границ отрезков (интервалов) в которых находятся корни кубического уравнения с действительными коэффициентами.

В данной статье предлагается способ, с помощью которого можно определить аналитический вид вершин таких границ.

Ключевые слова: кубическое уравнение, действительные корни, многочлен, конечные промежутки, аналитический, границы.

It is known that the solution of some theoretical and practical problems, as well as the modeling of certain physical processes, requires the determination of the boundaries of segments (intervals) in which the roots of a cubic equation with real coefficients are located.

In this article, we propose a method by which we can determine the analytical form of the vertices of such boundaries.

Keywords: cubic equation, real roots, polynomial, finite intervals, analytic, boundaries.

Нахождение конечных отрезков, в которых может находиться каждый из действительных корней, имеет большое практическое значение для инженеров.

Существуют различные методы решения кубических уравнений. Эти методы разделяются на аналитические (точные) и численные. Аналитическим методам относятся метод Карно, тригонометрический способ Виета, использование возвратных уравнений и т. д. [1,2,3].

Численным методам можно отнести методы Ньютона (касательных, хорд и их совместное применение) [1,2], метод Горнера, Лобачевского, метод итерации, деления отрезка пополам, метод скоростного спуска и т. д. Каждый из этих методов имеют свои плюсы и минусы.

Предложенный мною способ находится как бы между точным и численным методами. Так что если кубическое уравнение имеет два или три одинаковых корня, то этот способ позволяет точно аналитическими формулами найти эти корни. Однако если кубическое уравнение имеет три различных действительных корней, то устанавливаются три интервала вершины которых задаются аналитически.

Аналитическое задании вершин интервалов в которых находятся действительные корни кубических уравнений позволяют установить пределы изменения физических параметров входящих в эти уравнения.

Как известно [1], для нахождения критических точек и интервалов возрастания и убывания мы поступаем следующим образом. Сначала делаем подстановку . Тогда получаем:

.

Пусть . Подставляяполучаем:

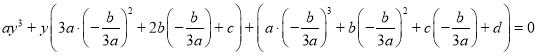
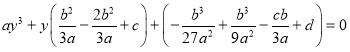
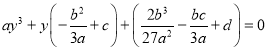
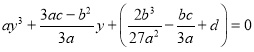
Следовательно, еслито

Другими словами прифункция возрастающая. А если возможно три случая:

1) в промежутке 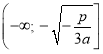функция возрастающая;

2) в промежутке 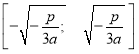функция убывающая;

3) в промежутке 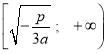функция возрастающая.

С другой стороны если подставитьито прифункция возрастающая, а при

а) в промежутке 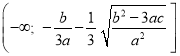функция возрастающая;

б) в промежутке 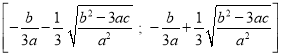функция убывающая;

с) в промежутке 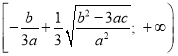функция возрастающая.

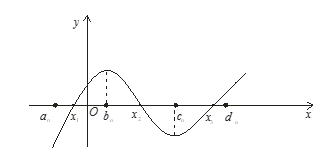
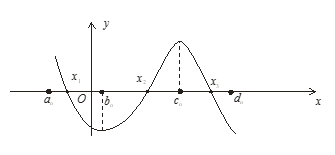
Таким образом понятно, что второй корень находится в промежутке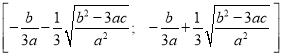.Предположим, что одним из корней уравненияявляется x_o.

Тогда,

или ,

Сравнивая последнее уравнение с уравнением , получаем:

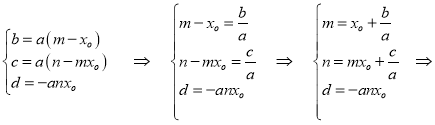
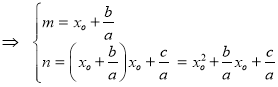
Таким образом, одним из корней является, другие две корня являются решением уравнения или .Для этого. Тогда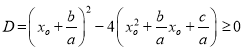

Определим промежуток, в котором находятся корни x_o: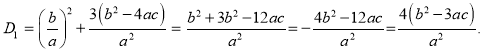Тогда

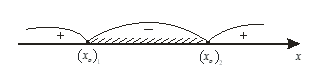
Как видно эти корни находятся в промежутке.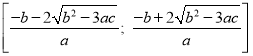

Пусть. Здесь.

Условие равенство возможно при.

Следовательно, при

при

А теперь предположим, чтоТогда . Здесь Следовательно

, здесь

.

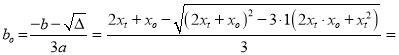
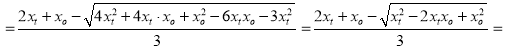
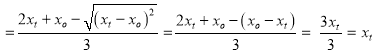Так как,то

Таким образом в этом случае получается

То есть

Аналогично можно показать чтo при

.

Если все три корни равны, тоЗдесь получаем

Так как , то В этом случаеКак видим, если два или все три корня равны, то они совпадают с одной из точек .Можно показать, что в этом случае график функции касается оси абсцисс.

Действительно, если функция имеет вид ,, тогдаиТаким образом в точке уравнение касательной будет. А это и есть уравнение абсциссы.

В этом случае график функции при

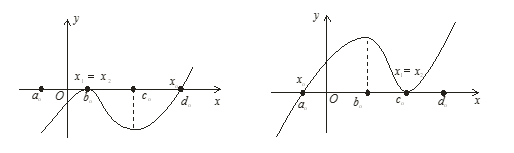
А при

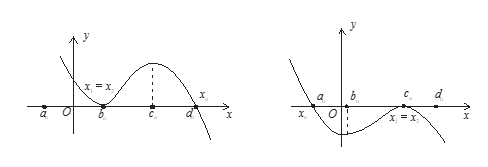
Таким образом, если нам дано уравнение в виде , то вычисляются значение выражений,D=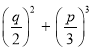и определяется знак D. Если Dто уравнение имеет три действительных корня. При этом если , то один из корней отрицательный, а если , то уравнение не имеет отрицательных корней. В случае когда 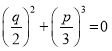, то график функции в одной точке пересекает, а в другой касается оси абсцисс то есть два корня совпадают. Если все три корня равны, то . А теперь рассмотрим случай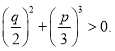В этом случаеи график функции с осью абсцисс имеет всего одну точку пересечения. Найдем абсциссу этой точки.

Пусть . Тогда

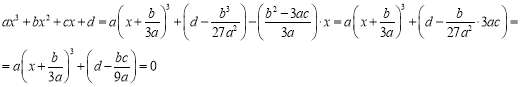
Отсюда получаемили.

Здесь, если ,то. В этом случае все три корня совпадают.

Это точка является точкой перехода. Действительно приполучаем , и в этой точке .

С другой стороны, так как

,то при получаеми. То есть в этой точке касательная совпадает с осью абсцисс и график функции является кубической параболой.

Рассуждая аналогическим образом, можно показать, что при и

1) если , то ;

2) если , то

здесь . А при и

1) единственный корень уравнения находится в промежутке ;

2) а при единственный корень уравнения находится в промежутке .

Таким образом, в данной статье предлагается способ, с помощью которого можно определить аналитический вид вершин границ отрезков (интервалов), в которых могут находиться корни кубических уравнений.

Литература:

1. Бронштейн И. Н., Семендяев К. А. Справочник по математике — Изд 7-е стереотипное. – М: Государственное издательство технико-теоретической литературы, — с.138–139.
2. Демидович Б. П., Марон И. А., Шувалова Э. З. Численные методы анализа — М.: Наука, 1968.
3. Копченова Н. В., Марон И. А. Вычислительная математика в примерах и задачах. — M.: Наука 1972.