Мультимодальное планирование маршрута, которое позволяет использовать несколько видов транспорта в одной поездке, становится все более популярным из-за сильного практического интереса и значительно возрастающих, в последнее время, информационных возможностей [1].
В реальной жизни транспортные сети характеризуются неопределенностью. Тем не менее, большинство подходов предполагают детерминированную среду, делая планы более склонными к сбоям, таким как: пропуск транспортных средства, а также серьезные задержки в прибытии различного транспорта.
В данной статье представлен подход к вычислению оптимальных планов маршрутов в мультимодальном планировании поездки. Проблема моделируется как поиск в пространстве состояний And/Or(далее AO*) [2]. В настоящей работе будут описаны улучшения поиска, используемые поверх алгоритма AO*. Усовершенствования включают в себя следующие основные моменты: дополнительные эвристические критерии для поиска не просто оптимального, но и надежного маршрута, метод, позволяющий снизить затрачиваемые для вычисления маршрута ресурсы компьютера, т. е. повышение производительности алгоритма, сохраняющий при этом полноту и оптимальность, а также гибридный подход поиска с детерминированным и недетерминированным поиском.
Общая схема алгоритма поиска маршрута
В этом разделе мы представляем гибридный подход к решению, который объединяет детерминированный и недетерминированный поиск. Это введено, чтобы ускорить процесс решения в трудных случаях. Идея проиллюстрирована на рисунке 1.
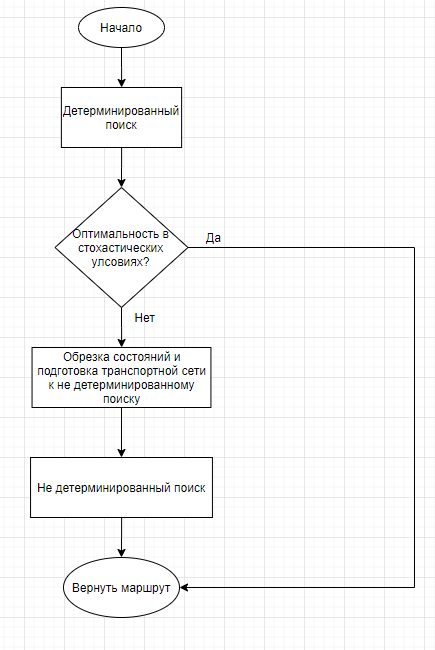
Рис. 1. Схема гибридного алгоритма
Гибридный поиск и обрезка состояний графа
Реальные транспортные сети на практике очень громадны и поскольку в нашем алгоритме второй шаг довольно ресурсозатратен, мы вводим обрезку состояний графа, для повышения производительности алгоритма. Таким образом, те состояния, которые являются бесполезными, и не будут иметь перспективных решений, в конце первого шага (при поиске алгоритмом А*) будут отброшены. Однако нам нужно суметь определить такие состояния.
В случае, если решения на первом этапе не находится, в нашей работе предлагается в любом случае определять эталонный детерминированный маршрут, на основе которого будет происходить обрезка состояний. Данный маршрут не будет являться решением на первом этапе, он необходим исключительно для обрезки графа.
Представим транспортную сеть, как на рисунке 2.
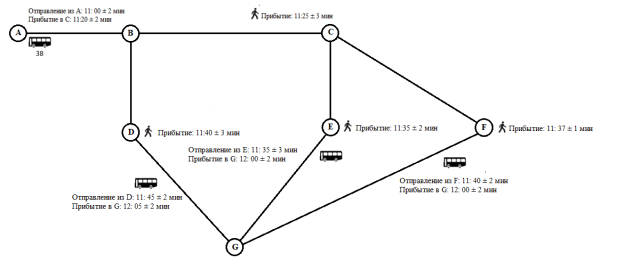
Рис. 2. Транспортная сеть № 2 с автобусом и пешеходом
В данном примере будут рассмотрены только состояния D и F, так как в них мы гарантированно попадаем на автобус (P(U < B) = 1), состояние E не рассматривается вообще. Таким образом, транспортная сеть может быть преобразована к следующему виду (Рисунок 3).
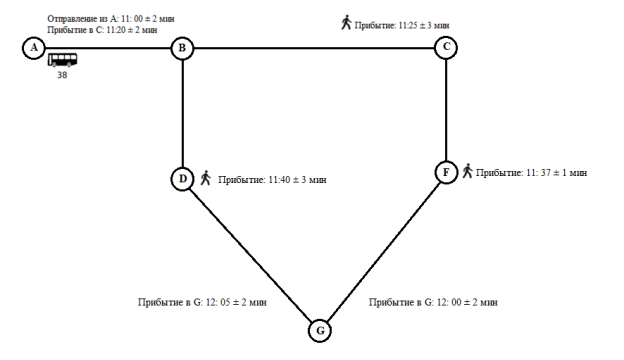
Рис. 3. преобразованная транспортная сеть № 2
Из данного примера видно, что задача сводится к детерминированной где, как и раньше мы также можем определить детерминированный маршрут.
В нашем случае пользователь будет двигаться по пути из таблицы 3.
Таблица 3
|
Траектория |
Шаги |
Итоговое время прибытия |
|
A → B → C → F → G |
11: 00 — сесть на автобус 38 до пункта «B» 11:20 — ходьба до пункта «C» 11:25 — ходьба до пункта «F» 11:37 — ходьба до пункта назначения «G» |
~ 12:00 |
Имея детерминированный маршрут, нам не придется рассматривать другие, которые будут давать нам хуже результат по времени при условиях недетерминированности, поскольку наш маршрут дает полную гарантию, что пользователь прибудет в пункт назначения в указанное время, в то время как другие маршруты не представляют такой возможности. Это означает, что на втором этапе поиска маршрута, более емким, наихудший вариант, который только может получиться, это маршрут, найденный ранее, и рассматривать состояния тех маршрутов, которые в условиях недетерминированности дают хуже результат, чем на первом шаге, будет просто не иметь смысла.
Формула (эвристическая формула оценки состояний), по которой происходит расчет на втором этапе, в общем виде выглядит следующим образом: 
,
где g(n) — стоимость пройденного пути,
h(n) — оценка расстояния от узла n до целевого узла.
Опишем следующие правила, оценивания функции 
:
1) В случае, если текущее состояние является целевым, значит полагаем, что 
;
2) В случае, если текущее состояние не позволяет ни каким образом достижение целевого состояния, значит полагаем, что 
3) В случае, если текущее состояние не относится к предыдущим пунктам, полагаем, что 
, где 
= 
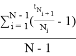
Учитывая состояние 
, A(
— это множество исходящих действий из состояния в недетерминированной области. Для данного действия 
- количество ветвей этого действия. Для детерминированного действия = 1. Для недетерминированного действия 
. 
— соответствующая вероятность, — коэффициент надежности (расхождения во времени маршрутов исходящих из этой точки), а 
— стоимость пути (время затрачиваемое на передвижение). Поскольку величина 
всегда больше 1 (т. к. 
номер следующего маршрута, по которому пойдет пользователь в случае не успеха сесть на автобус, а значит такой маршрут будет иметь заведомо больше времени для достижения цели), следовательно, 
будет положительным. Здесь в качестве N отмечается N-ый номер маршрута, а 
- время, затрачиваемое при достижении конечной цели следуя по этому маршруту.
Литература:
- Adi Botea, Akihiro Kishimoto, Elizabeth Daly (2016). Combining Deterministic and Nondetermenistic Search for Optimal Journey Planning Under Ucertainty.
- Nikolova, E.,Brand, M., & Karger, D.R.(2006). Optimal route planning under uncertainty. In Long, D., Smith, S.F., Borrajo, D., & McCluskey, L.(Eds.), Proceedings of the 16nd International Conference on Automated Planning and Scheduling (ICAPS), 131–141.
- Holte, R., Perez, M., Zimmer, R., & MacDonald, A.J. (1995). Hierarchical A*: Searching abstraction hierarchies efficiently. Tech. rep., Department of Computer Science, University of Ottawa.
- Hoffmann, J., & Brafman, R. (2005). Contingent planning via heuristic forward search with implicit belief states. In Proceedings of the 15th International Conference on Automated Planning and Scheduling (ICAPS-05), 71–80.
- Nikolova, E., Kelner, J.A., Brand, M., & Mitzenmacher, M. (2006). Stochastic shortest paths via quasi-convex maximization, 552–563.
