Данная статья посвящена анализу работы вантовых элементов конструкций с внешним сосредоточенным демпфером. В рамках данной работы был произведен расчет собственных колебаний струны путем численного анализа собственных значений струны с одним демпфером вблизи опоры и получены графики зависимости скорости и перемещений от времени. Одной из основных задач динамического расчета является уменьшение колебаний, так как ванты имеют довольно низкую собственную демпфирующую способность.
Ключевые слова: колебания вант, вантовые мосты, собственные колебания, внешний сосредоточенный демпфер.
Наиболее традиционный способ ограничения или устранения колебаний ванта заключается в увеличении их конструктивной демпфирующей способности путем установки специальных устройств.
Существует несколько видов демпферов:
– внешние демпферы: это, как правило, гидравлические устройства, оказывающие поперечное демпфирующее усилие на трос, вблизи опор. Общий вид такого демпфера на Русском мосту представлен на Рис. 1.
– внутренние демпферы: размещаются между тросом и стальной трубой, жестко прикрепленной к конструкции опоры. Внутренние демпферы используют искажение рассеивающего материала или вязкое трение. Общий вид внутреннего демпфера показан на Рис. 2.
|
|
|
|
Рис. 1. Внешний демпфер на Русском мосту (г. Владивосток) |
Рис. 2. Внутренний демпфер на Живописном мосту (г. Москва) |
Основной задачей данной работы является анализ работы вантового элемента с установленным внешним сосредоточенным демпфером и сравнение результатов колебаний с расчетной схемой, в которой учтено только собственное внутреннее демпфирование.
Для оценки влияния внешнего сосредоточенного демпфера на колебания вант использован метод явного интегрирования уравнения движения:
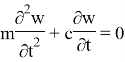
Представим вант как струну, шарнирно закрепленную по концам с опорами в одном уровне равномерно загруженной собственным весом с одним демпфером вблизи опоры на расстоянии ![]() . На Рис. 3 представлена расчетная схема струны. Для решения поставленной задачи приняты необходимые исходные данные (таблица 2).
. На Рис. 3 представлена расчетная схема струны. Для решения поставленной задачи приняты необходимые исходные данные (таблица 2).
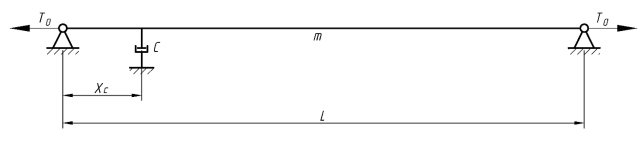
Рис. 3. Расчетная схема ванта с внешним сосредоточенным демпфером
В данной задаче при расчете колебаний ванта, также учтено собственное демпфирование за счет внутреннего трения.
Таблица 1
Исходные данные
|
Длина ванты |
Удельный вес |
Площадь поперечного сечения |
Модуль Юнга |
Скорость распространения волны |
Натяжение |
Основная угловая частота |
Постоянная демпфирования |
|
100,0 |
7850,0 |
0,012 |
2,06∙108 |
300,0 |
4905,0 |
7,169 |
400,0 |
Для того, чтобы определить собственные колебания струны, зададим системе возмущение в момент времени ![]() в виде начальной скорости
в виде начальной скорости ![]() . Струну длинной
. Струну длинной ![]() разделим на
разделим на ![]() равных частей с шагом
равных частей с шагом ![]() , тем самым получаем
, тем самым получаем ![]() узлов в нашей системе. Также зададимся временным шагом. Они должны быть достаточно малыми, чтобы избежать численной погрешности.
узлов в нашей системе. Также зададимся временным шагом. Они должны быть достаточно малыми, чтобы избежать численной погрешности.
![]() м
м
![]() сек,
сек,
После выведения системы из равновесия для реализации метода необходимо выполнить последовательно на каждом временном шаге во всех узлах системы расчет следующих величин, характеризующих колебательное движения туго натянутой струны:
-
Начальную скорость
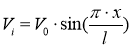 , первую форму колебаний описывает закон синусоиды.
, первую форму колебаний описывает закон синусоиды.
-
Имея скорости в явном виде, вычислим во всех узлах системы смещение
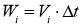 .
.
- Спроецируем все действующие силы в узле на ось Y и получим выражение для определения силы действующей на узловую сосредоточенную массу и соответствующее ей ускорение:
![]() ;
;
![]() .
.
-
Далее вычислим приращение скорости
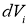 и определим результирующую скорость
и определим результирующую скорость 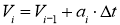 .
.
-
Для
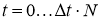 , следуя выше изложенному алгоритму, вычислим на каждом временном шаге неизвестные параметры.
, следуя выше изложенному алгоритму, вычислим на каждом временном шаге неизвестные параметры.
Для учета внутреннего демпфирования в каждом узле системы дополнительно приложим силу демпфирования
где ![]() — постоянная вязкого демпфирования;
— постоянная вязкого демпфирования;
![]() — коэффициент демпфирования;
— коэффициент демпфирования;
![]() — логарифмический декремент для собственного демпфирования.
— логарифмический декремент для собственного демпфирования.
Для учета внешнего демпфера также приложим силу ![]() , только уже в одном определенном узле системы вантового элемента, в зависимости от
, только уже в одном определенном узле системы вантового элемента, в зависимости от ![]() . Данная задача решается численно с применением среды Matlab, так как расчёты получаются очень трудоемкими, в связи с малым дискретным шагом по времени
. Данная задача решается численно с применением среды Matlab, так как расчёты получаются очень трудоемкими, в связи с малым дискретным шагом по времени ![]() .
.
В результате расчета построим графики зависимости скорости и перемещений от времени (Рис. 4). Видно, что с течением времени происходит затухание колебаний, при чем при С=0, т. е. учитывается только собственное демпфирование, этот процесс протекает медленнее.
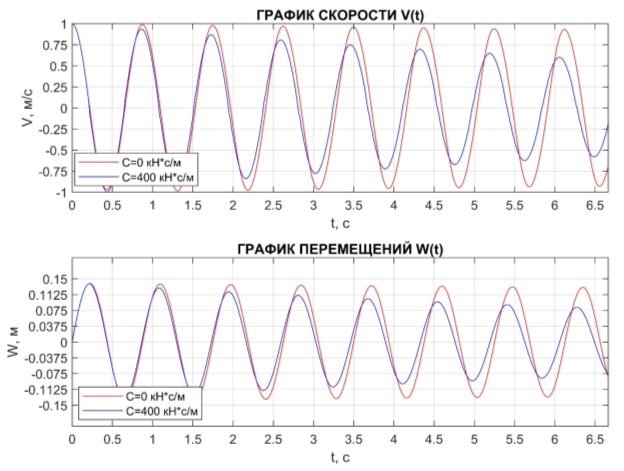
Рис. 4. График зависимости скорости ![]() и перемещений
и перемещений ![]() от времени
от времени ![]() при Xc=2,0 м
при Xc=2,0 м
Для того, чтобы численно оценить разницу между двумя вариантами: с внешним сосредоточенным демпфером и без него, вычислим логарифмический декремент, как натуральный логарифм отношения двух последовательных амплитуд свободных колебаний:
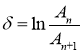
Тогда получим для варианта с учетом внешнего сосредоточенного демпфера — ![]() , а соответственно только с учетом собственного демпфирования —
, а соответственно только с учетом собственного демпфирования — ![]() .
.
Наглядно видно, что колебания вантового элемента с учетом внешнего сосредоточенного демпфера затухают намного быстрее. Так при использовании демпфера на расстоянии от опоры
В целом, следует сделать вывод, что метод использованный в данной работе при расчете колебаний ванта с учетом внешнего сосредоточенного демпфера может быть использован при проектировании вантовых элементов конструкций.
Также хотелось бы отметить, что в дальнейшем для более точной оценки колебаний вантовых элементов необходимо учесть геометрическую нелинейность, рассмотреть расчетную схему с учетом провисания, это позволит приблизиться к реальной работе вантового элемента.
Литература:
- Вантовые мосты / А. А. Петропавловский, Е. И. Крыльцов, Н. Н. Богданов и др.; Под ред. А. А. Петропавловского. — М.: Транспорт, 1985. — 224 с.
- Меркин Д. Р. Введение в механику гибкой нити. — М.: Наука. Главная редакция физико-математической литературы, 1980. — 240 с.
- Качурин В. К. Гибкие нити с малыми стрелками. — М.: Гос. издательство технико-теоретической литературы, 1956. — 224 с.
- Cable stays. Recommendation of French interministerial commission on Prestressing. — CIP Setra, 2002. — 197 p.
- Elsa de Sá Caetano. Cable Vibrations in Cable-Stayed Bridges. — IABSE-AIPC-IVBH, 2007. — 188 p.









