Развитие военного дела, постоянное совершенствование вооружения и специальной техники в интересах обороноспособности нашей страны выдвинули перед высшими военными учебными заведениями сложную и важную задачу — в ограниченный срок обучения подготовить для войск высококвалифицированного специалиста, умеющего самостоятельно добывать знания, способного в сжатые сроки осваивать их новые образцы, профессионально решать поставленные задачи, ориентироваться в стремительном потоке научной и учебной информации, идти в ногу с военно-научными достижениями. В связи с этим значительно усиливается значение и роль внеаудиторной самостоятельной работы курсантов военных ВУЗов, в часы которой обучающийся может принимать участие в военно-научной работе (ВНР).
В нашем вузе ВНР курсантов организуется в тесной взаимосвязи с образовательным процессом и проводится в соответствии с нормативными и правовыми документами Российской Федерации и локальными актами МО РФ с целью развития у обучающихся творческого мышления и самостоятельности, углубления и закрепления полученных при обучении знаний, формирования интереса к военно-научному творчеству, обучения методике и способам самостоятельного решения научно-технических задач. Формами работы являются: выполнение заданий исследовательского характера, участие в изобретательской и рационализаторской работе, разработке и создании действующих стендов, макетов и моделирующих комплексов, написании рефератов, выступлении на конференциях и прочее. [1]
Активизация самостоятельной работы курсантов в рамках ВНР определяется пониманием поставленных перед ними задач, имеющих практическое значение в образовательном процессе. Она может проявиться в учебно-познавательной деятельности, результатом которой станет создание проекта, представляющего интегративное дидактическое средство обучения, воспитания и развития, и позволяющего сформировать ряд учебных компетенций.
Колебательные процессы очень часто встречаются в природе и технике. Они проявляются, например, при запуске авиационных двигателей, вибрациях винтов, динамике циклонов, влияющих на обеспечение безопасности полетов любых летательных аппаратов, движении поршней двигателей внутреннего сгорания, колебаний фундаментов и строительных конструкций. Колебаниями являются звуковые и электромагнитные волны, переменный ток.
Разнообразие и широкое распространение колебательных процессов в технических устройствах специального назначения делают значимым и необходимым для любой специальности нашего ВУЗа изучение теории колебаний. Физика колебаний базируется на исследовании поведения гармонического осциллятора с одной степенью свободы, например, математического маятника в однородном поле тяготения. Эта целостная физическая модель, имея границы применения, позволяет установить сходство модели и оригинала по ряду признаков, заменять действительный объект физической моделью, экстраполировать полученную информацию при изучении модели на реальный физический объект.
Колебательные процессы, несмотря на техническое разнообразие колебательных систем и процессов, характера воздействия на колебательную систему (свободные и вынужденные) описываются одинаковыми дифференциальными уравнениями второго порядка и характеризуются похожими параметрами: частотой, периодом, амплитудой, фазой.
Свободные колебания могут быть незатухающими только в идеальной колебательной системе без потерь энергии, где не действуют диссипативные силы. В реальных колебательных системах всегда существуют потери энергии. В них колебания будут затухающими, если нет подвода энергии извне. Если величина диссипативных сил не слишком значительна, то система совершает практически периодическое движение с экспоненциально убывающей амплитудой и постоянной частотой в условиях неизменной температуры окружающей среды.
Мы выбрали монопроект по физике, который по характеру преобладающей деятельности является практико-ориентированным, чтобы создать наглядную модель для изучения физики колебаний и демонстрации картины фаз гармонических колебаний.
Целью нашего проекта стало решение практической задачи изучения свободного затухающего гармонического колебания на примере математического маятника.
Частота и период колебаний математического маятника определяются только длиной нити и ускорением свободного падения в данной области пространства в случае свободных колебаний при небольшой скорости затухания. Амплитуда затухающих колебаний уменьшается с течением времени тем быстрее, чем больше коэффициент затухания 
. Для математического маятника он определяется выражением:
,(1)
где 
коэффициент сопротивления среды; 
масса маятника; 
время релаксации, т. е. время, в течении которого амплитуда колебаний уменьшилась в е = 2,72 раза.
Колебания в механических системах сопровождаются периодическими превращениями механической энергии колеблющихся тел в потенциальную энергию взаимодействия частей системы и обратно. Если система изолирована от внешних воздействий, и колебательное движение происходит в отсутствии диссипативных сил (трение, сопротивление окружающей среды), то с течением времени ее полная механическая энергия не меняется. В реальных системах она может уменьшаться не только вследствие трения, но и при наличии излучения упругих волн.
Для количественной характеристики потери энергии используют добротность, логарифмический декрементом затухания.
Добротность колебательной системы представляет собой безразмерную величину, прямо пропорциональную энергии 
в произвольный момент времени 
и обратно пропорциональную величине убыли этой энергии за промежуток времени от 
до 
:
.(2)
Энергия прямо пропорциональна квадрату амплитуды 
, следовательно,
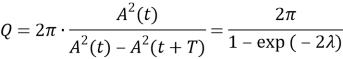,(3)
где логарифмический декремент затухания.
Логарифмический декремент затухания определяется по формуле:
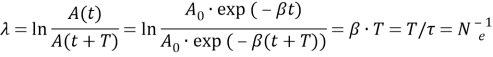, (4)
где
начальная амплитуда колебаний; 
число колебаний за время релаксации ; Т период затухания, 
; 
циклическая частота. Для математического маятника длиной L циклическая частота определяется выражением:
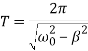. (5)
При малых затуханиях 
, считая, что период колебаний постоянная величина, знаменатель выражения (3) примет вид: 
.
На основании этого преобразовав математически равенство (3), получим:
,(6)
где коэффициент затухания.
Согласно формулам (3, 4), чем больше логарифмический декремент затухания , тем быстрее происходит затухание колебаний и тем меньше добротность Q колебательной системы. Следовательно, добротность определяет ее способность сохранять колебания. Этот параметр характеризует во сколько раз запасы энергии больше, чем потери энергии за время изменения фазы на один радиан.
Для малых затуханий энергия осциллятора с течением времени меняется по закону:
,(7)
где начальная энергия 
/2; начальная амплитуда колебаний. Для математического маятника массой коэффициент пропорциональности определяется выражением 
.
Выразив коэффициент затухания из формулы (7), получим
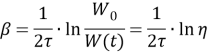.(8)
В нашем проекте математические маятники имеют нити различной длины, т. е. разные частоты колебаний, и одинаковые массы шариков. С их помощью можно наглядно получить картину фаз всех маятников во времени и продемонстрировать затухающие механические колебания 15 гармонических колебаний одного направления, но разных периодов колебаний. Для этого в эксперименте следует отклонить их на одинаковый угол от положения равновесия (например, линейкой) и привести в колебательное движение.
Наблюдаемые колебания будут свободными гармоническими только при соблюдении двух условий: 1) нерастяжимость нитей подвеса; 2) малый угол отклонения от положения равновесия за счет внесенной энергии в замкнутую систему.
Чтобы колебания всех 15 маятников происходили в одной плоскости, каждый шарик подвешен на двух нитях одинаковой длины, расположенных под небольшим углом друг к другу на прочно укрепленной раме. Длины нитей отличались приблизительно на 1 см. Мы определили число колебаний и время релаксации при движении соседних маятников разной длины в одном направлении. Затем провели косвенные измерения логарифмического декремента затухания и добротности Q колебательных систем. Данные представлены в таблице.
Таблица
Параметры 15 осцилляторов содной степенью свободы
|
№ |
L, см |
, с |
Ne |
|
Q |
|
1 |
21 |
51 |
26 |
0,0384 |
81 |
|
2 |
22 |
59 |
30 |
0,0333 |
94 |
|
3 |
23 |
79 |
39 |
0,0256 |
122 |
|
… |
… |
… |
… |
… |
… |
|
14 |
34 |
124 |
52 |
0,0192 |
163 |
|
15 |
35 |
124 |
53 |
0,0189 |
166 |
На графиках (рис.1–3) представлены исследуемые параметры. Небольшие отклонения связаны с погрешностью обработки результатов. Линия тренда описана линейной зависимостью у(х).
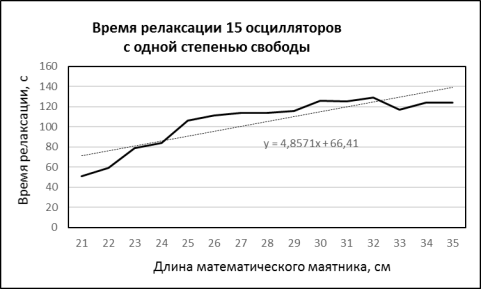
Рис.1. Моменты времени релаксации 15 осцилляторов с одной степенью свободы
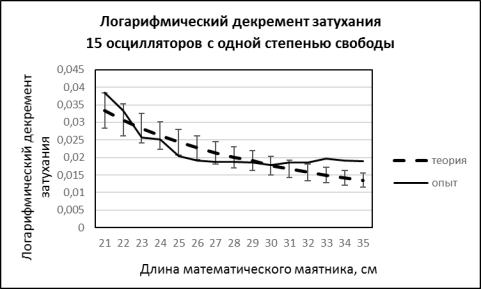
Рис.2. Логарифмический декремент затухания 15 осцилляторов с одной степенью свободы
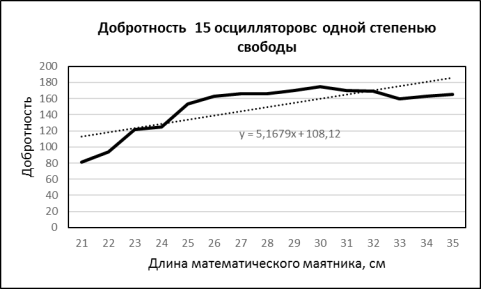
Рис.3. Добротность 15 осцилляторов с одной степенью свободы
Таким образом, проведенные исследования показали, что модель из 15 математических маятников можно использовать для демонстрации картины фаз гармонических колебаний маятников.
Литература:
- http://xn----7sbajajhyox3duj.xn--p1ai/nauka/voenno-nauchnaya-rabota.html.
