Работа посвящена моделированию одноопорной двухмассовой колебательной системы, изображающей автомобиль с фрактальной подвеской, содержащей регулируемый демпфер. Приведена расчетная схема и общая модель данной колебательной системы, а также варианты регулирования демпфирования.
Ключевые слова: колебательная система, подрессоренная масса, дополнительный дроссельный канал, проходное сечение, маятниковый регулятор, коэффициент демпфирования амортизатора, регулируемый амортизатор, математическая модель.
На рис. 1 представлена расчетная схема одноопорной двухмассовой колебательной системы, изображающей автомобиль с фрактальной подвеской, содержащей регулируемый амортизатор.
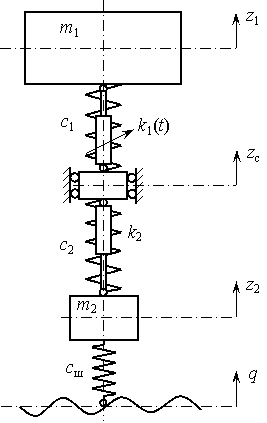
Рис. 1. Одноопорная двухмассовая колебательная система, изображающая автомобиль с фрактальной подвеской, содержащей регулируемый амортизатор: m1 — подрессоренная масса; m2 — неподрессоренная масса; 
— жесткость упругого элемента верхней фракции подвески; 
— жесткость упругого элемента нижней фракции подвески; 
— коэффициент демпфирования амортизатора верхней фракции подвески; 
— коэффициент демпфирования амортизатора нижней фракции подвески; q — кинематическое возмущение; z1 — перемещение подрессоренной массы; z2 — перемещение неподрессоренной массы; zс — перемещение соединительного узла фракций подвески
Математическая модель одноопорной двухмассовой колебательной системы, изображающей автомобиль с фрактальной подвеской, содержащей регулируемый амортизатор, имеет следующий вид.
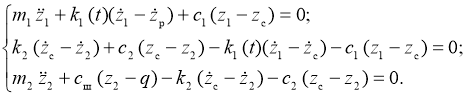
Управление амортизатором возможно по двум алгоритмам. Первый алгоритм является оптимальным для минимизации вертикальных перемещений подрессоренной массы:
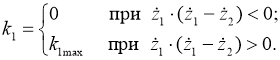
Как видно из приведенного выражения, этот алгоритм осуществляет мгновенное изменение коэффициента демпфирования амортизатора.
Второй алгоритм можно реализовать с помощью специального маятникового регулятора, встроенного в амортизатор (рис. 2).
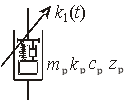
Рис. 2. Маятниковый регулятор демпфирования:
mр — масса регулятора; k1(t) — коэффициент демпфирования амортизатора; zр — перемещение регулятора; cр — жесткость регулятора; kр — коэффициент демпфирования регулятора
Принцип работы маятникового регулятора заключается в следующем. В амортизаторе имеется два дроссельных канала — основной и дополнительный. Основной дроссельный канал постоянно открыт. На пути движения жидкости через дополнительный дроссельный канал установлен золотник. Маятник в виде подпружиненного груза, закрепленный на корпусе автомобиля, совершает колебания с частотой возмущающего воздействия и управляет золотником дополнительного канала. При нейтральном положении маятника дополнительный дроссельный канал имеет максимальное проходное сечение. При перемещении маятника от нейтрального положения на некоторую величину золотник полностью перекрывает дополнительный дроссельный канал. Маятник имеет регулируемый демпфер, которым можно изменять сдвиг фаз колебаний маятника относительно колебаний подрессоренной массы.
В этом случае k1(t) — величина, зависящая от площади проходного сечения дроссельных каналов:
.
Здесь μ — коэффициент, зависящий от параметров амортизатора. Общая площадь S проходного сечения дроссельных каналов меняется по закону:
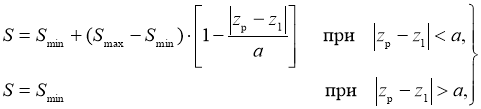
где
— площадь проходного сечения основного дроссельного канала;
— общая площадь проходного сечения дроссельных каналов при полностью открытом дополнительном дроссельном канале;
a — минимальное значение величины перемещения маятника относительно рессоры, при котором дополнительный дроссельный канал полностью закрыт.
Колебания маятника происходят по закону:
.
Маятниковый регулятор осуществляет немгновенное переключение неупругого сопротивления.
Исследование регулирования амортизатора по первому алгоритму при синусоидальном возмущении показало существенное уменьшение вертикальных перемещений и ускорений подрессоренной массы практически во всем диапазоне рабочих частот. Однако этот алгоритм трудно реализуем при движении машины по реальному дорожному профилю. В этом случае возможно использование маятникового регулятора, работа которого подлежит дальнейшему исследованию.
