Высокие уровни вибраций и шумов на подвижных объектах, вызванные непрерывным ростом мощностей двигательных установок и повышенными скоростными характеристиками, имеют широкую полосу частот. Поэтому проблемы устранения вибраций в РЭА (радиоэлектронной аппаратуры), особенно резонансных явлений в элементах конструкций, становятся важными ещё на этапе проектирования. Традиционные методы борьбы с вибрацией не обеспечивают выполнения функциональных задач РЭА на объекте в условиях, когда требуются низкий уровень виброшумов, моль масса, повышенные надёжность и долговечность при высокий интенсивности механических воздействий.
В настоящей статье описывается использование полимерных материалов для рассеяния энергии колебаний в конструкциях РЭА.
В работе рассматриваются установившиеся колебания. Конструкция состоит из четырёх упругих стрежней с несколькими жесткими массами. Пространство между стержнями заполнено полимерными материалами.
Уравнения движения получены с помощью метода конечных элементов, которые имеют следующий вид:
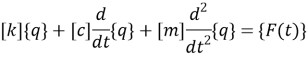(1)
где
– матрица масс; 
– матрица демпфирования; t – время; 
– неизвестный вектор столбец; 
– матрица жёсткости; 
– внешние воздействия вектор столбец; 
; 
– постоянная величина; W – частота внешних воздействий. Далее предположим, что решение – существует и имеет вид:
После подстановки этих выражений в (1) получим:
(2)
Решение уравнения (1) относительно
дает возможную форму колебаний механической системы.
В общем случаи и 
будем считать комплексными, тогда уравнение (1) можно рассматривать как совокупность двух уравнений, получающих в результате приравнивания вещественных и мнимых частей. Таким образом, если
где все величины с одной и двумя черточками сверху вещественные, то приравнивая вещественную и мнимую части получаем систему двух уравнений, которую можно записать с матричном виде:
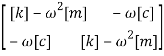
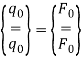(3)
Уравнения (3) образуют систему, в которую входят только вещественные величины. В результате решения этой системы можно определить реакцию при любых периодических возмущениях. Система состоит из абсолютно жестких масс mi и (i = 1,2...24) деформируемых сред. На нижнее основание воздействует вибрационная нагрузка.
Для решения поставленной задачи используется метод конечных элементов. Системы алгебраических уравнений (3) решаются в работе методом Гаусса с выделением главного элемента.
Если на систему внешние возмущения отсутствуют; то решение уравнения (1) отражается в виде:
(4)
где 
– комплексная форма колебаний; 
– искомая комплексная частота. Задача сводится к решению однородных алгебраических уравнений:
(5)
Решения поставленной задачи на собственные значения осуществляются методом. Мюллера без выделения комплексного параметра в явном виде.
В расчетах варьируются модель упругости Е, параметров вязкости и др. параметры.
;
;
Для того чтобы выполнить численные расчеты, необходимо задавать жесткость. К и коэффициент потерь элемента для материала в виде сильно демпфирующего свойства.
Установлено, что при сближении пар частот II-III, IV-V значений величины E2 = 2.17 1010 H/м2, соответствующие этим частотам коэффициенты демпфирования (при том же значении параметра) пересекаются между собой. Коэффициент демпфирования 
прямо связанный с логарифмическим декрементом затухания, служит мерой рассеяния энергии процесса. Наибольший практический интерес в решении поставленной задачи представляет минимальное значение коэффициента демпфирования.
Минимальное значения коэффициента демпфирования для сближающейся пары частот дает информацию о скорости затухания того тона колебаний упругого стержня — I, который медленнее демпфируется, следовательно, является определяющим. Также установлены обобщенные таким образом коэффициенты демпфирования для второго и третьего тонов колебаний стрежня I; в области максимального сближения частот имеет место ярко выраженный обобщенный максимум диссипативных свойств. Значения коэффициента деформирования в приведенном интервале изменяется более чем на порядок.
Литература:
- Зенкевич О. Метод конечных элементов в технике. М: Мир, 1975 г.
- Ильинский В. С. Защита РЭА от динамических воздействий. М. Радио и связь, 1982. – 296 с.
