In the work described construction of vibradamping gaskets with a dry friction for the reduction of noise from saw disk circular woodworking machines. And also led, the mathematical model of reduction of level of noise pressure (∆L, dB) is radiated by saw disk with vibradamping gaskets with a dry friction. The mathematical model of reduction of level of noise pressure confirms the before conducted model tests and general acoustic efficiency of an offer construction.
The unified construction of the device which consists of the vibradamping frictional gaskets (with a dry friction VDPST) placed between a saw disk and a clamping flange circular of woodworking machines is offered. Introduce construction consist, in the least, from two identical vibradamping gaskets, consisted from ply base ply finely divided minerals abrasive particles, applied adhesion method on base. That said friction content joint surfaces expended in more than once at one's cost relative to penetration abrasive particles ply gaskets, what expended their acoustical efficiency. Crucial factor dissipation vibration energy in propose construction come out dry friction between minerals abrasive particles.
Key words: vibradamping, noise reduction, circular woodworking machine, gaskets with dry friction, saw disk, abrasive particles, mathematical model of reduction of noise
Как известно, круглопильные деревообрабатывающие станки относятся к одному из наиболее шумных видов деревообрабатывающего оборудования (уровень шума на рабочем ходу достигает 110–120 дБА). Доминирующим источником шума от круглопильных деревообрабатывающих станков на рабочем ходу является пильный диск, вследствие возбуждения в нем звуковой вибрации [1, 2, 3, 4, 5, 6].
Разработана и запатентована конструкция унифицированных вибродемпфирующих прокладок с сухим трением (ВДПСТ), которые помещаются между пильным диском и зажимными фланцами станка (рис. 1). Предлагаемая конструкция состоит, по меньшей мере, из двух идентичных вибродемпфирующих прокладок, состоящих каждая из слоя основы (например, тканевой или бумажной) и слоя мелкодисперсных минеральных абразивных частиц, наносимых адгезионным способом на основу. При этом фрикционная площадь контактирующих поверхностей увеличивается в несколько раз за счет взаимного проникновения мелкодисперсных частиц слоев прокладок, что позволяет повысить их акустическую эффективность, при этом ограничить их размер до диаметра зажимного фланца [7, 8, 9, 15].
Для пильного диска с ВДПСТ на сегодняшний день не существует подходов теоретического представления диссипации колебательной энергии в системе «пильный диск — ВДПСТ», что необходимо для теоретической оценки акустической эффективности предложенной конструкции нового демпфирующего устройства. На основе метода волнового сопротивления тонких пластин была разработана математическая модель снижения уровня звукового давления (∆L, дБ) излучаемого пильным диском с ВДПСТ [10, 11, 12, 13, 14,15]. При разработке модели были приняты некоторые допущения:
− пильный диск представлен как круглая металлическая пластина зажатая в центре;
− ВДПСТ представлены как пластины круглой формы зажатые в центре.
В данной работе приводится сокращенный вариант описания математической модели снижения шума от пильного диска применением ВДПСТ, в котором отражены основные подходы и положения моделирования [15].
Как известно, снижение шума излучаемого демпфированным пильным диском в окружающее пространство, оценивается по формуле:
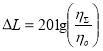,(1)
где ηo — коэффициенты потерь пильного диска без ВДПСТ; ηΣ — коэффициенты потерь пильного диска с ВДПСТ.
Коэффициент потерь материала пильного диска можно определить, если известен импеданс для данной конструкции по формуле (2), т. е.
(2)
где 
— модуль импеданса пильного диска; 
— действительная часть импеданса пильного диска; 
— мнимая часть импеданса пильного диска.
Коэффициент потерь материала пильного диска с ВДПСТ можно определить, если известен суммарный импеданс
(3)
где 
— модуль импеданса пильного диска с ВДПСТ; 
— действительная часть импеданса пильного диска с ВДПСТ; 
— мнимая часть импеданса пильного диска с ВДПСТ.
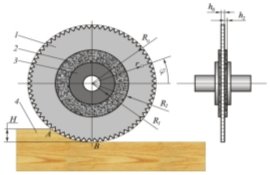
Рис. 1. Узел крепления пильного диска с ВДПСТ: 1 — пильный диск; 2 – ВДПСТ; 3 — зажимные фланцы; 4 — заготовка
Суммарный импеданс пильного диска с ВДПСТ имеет вид
(4)
где Z2 — импеданс ВДПСТ.
Импеданс пильного диска и ВДПСТ можно записать в виде
(5)
(6)
(7)
Составляющие суммарного импеданса пильного диска и ВДПСТ будут
(8)
(9)
На основании формулы (3) коэффициенты потерь, соответственно, для пильного диска с ВДПСТ будут:
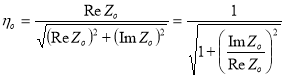(10)
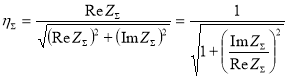(11)
Формулу (1) с учётом (8), (9), (10) и (11) после преобразований запишем в виде:
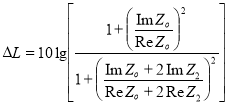(12)
Коэффициенты потерь, входящие в (1) и составные элементы импедансов, входящие в (12) могут быть определен на основе гипотез Кирхгофа-Лява [10, 11, 12,13,14]: прямолинейный элемент, нормальный к срединной поверхности до деформации, остается прямым и нормальным к срединной поверхности, не меняя своей длины. Деформации предполагаются малыми. В пластине реализуется обобщенное плоское напряженное состояние.
Деформацию срединной поверхности при изгибе пластины не учитывают. Предполагаем, что на пильный диск действует динамическая нагрузка F, а на контуре приложены поперечные силы, изгибающие и крутящие моменты. Согласно (8, 11, 12, 13, 15, 16, 18, 19, 20).
Поперечные колебания упругой пластины круглой формы описываются уравнением:
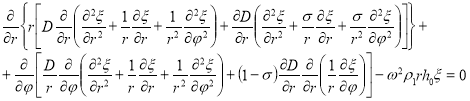(13)
где 
— цилиндрическая жесткость, в которой учтен коэффициент потерь материала дисковой пилы; r — радиальная координата точки на диске; φ — угловая координата точки на диске; ξ — поперечные перемещения диска пилы; ω — круговая частота колебаний диска; ρ1 — объемная плотность материала диска; ho — толщина диска; 
— мнимая единица.
С учетом динамической силы уравнение (13) после дифференцирования по времени, и выполнения некоторых преобразований, примет вид
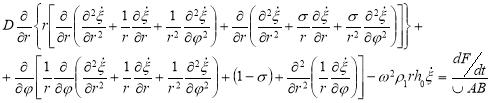(14)
где 
— вибрационная скорость поверхности диска.
Общее аналитическое решение уравнения (14) для вибрационной скорости может быть найдено в некоторых частных случаях с учетом некоторых допущений.
Во внимание будут приниматься условия:
1) Функция 
, что соответствует наличию только узловых окружностей и отсутствию узловых диаметров в собственных формах колебаний диска, т. е. 
2) Поверхность элемента диска носит колебательный характер в форме
, где ω — круговая частота колебаний;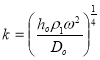 
— волновое число изгибных волн; 
— цилиндрическая жесткость пильного диска; Eo — модуль Юнга материала пильного диска; ηo — коэффициент потерь материала пильного диска.
3) Вибрационная скорость поверхности пильного диска с учётом (15) будет
(16)
4) Величина силовой нагрузки, действующей на пильный диск, будет определяться параметрами пильного диска, т. е. количество режущих зубьев, скорость вращения диска, глубина резания, ширина полотна диска и т. д. Величину силовой нагрузки можно представить в виде
(17)
где А — комплекс, учитывающий параметры диска и имеющий вид
(18)
где n — количество оборотов в минуту; z — количество режущих зубьев на диске,
— амплитуда силовой нагрузки; Np — мощность резания; Vp — скорость резания.
После ряда преобразований [15] из уравнений 11, 2 и с учетом 17 можно определить вибрационную скорость импеданс пильного диска, соответственно, в следующем виде:
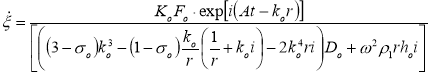(19)
где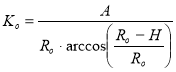 
(20)
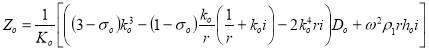(21)
Импеданс Z2 ВДПСТ можно определить на основании рассуждений представленных выше. Используем уравнение похожее на уравнение (14), но имеющее несколько иные характеристики материала. Уравнение поперечных колебаний ВДПСТ с учётом динамической силы представится в виде:
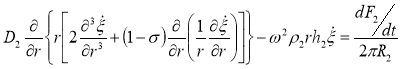(22)
Вибрационная скорость ВДПСТ определится из уравнения:
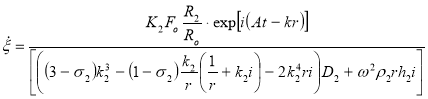(23)
Импеданс ВДПСТ запишем в виде
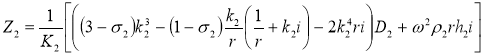(24)
В результате некоторых преобразований [15] мнимая и действительные части импедансов пильного диска и ВДПСТ примут следующий вид:
(25)
(26)
(27)
(28)
Зная значения импедансов, а соответственно и коэффициентов потерь пильного диска и ВДПСТ по формулам 1 и 12 можно рассчитать теоретическое снижение шума от применения ВДПСТ, где будет учитываться основные параметры: глубина резания, диаметр пильного диска, диаметр ВДПСТ, число зубьев пильного диска, количество оборотов пильного диска в минуту и. д.
По разработанной математической модели были проведены расчеты снижения уровней звукового давления от возбужденного пильного диска применением ВДПСТ. Основные параметры, использованные для теоретических расчетов, соответствовали параметрам, при которых проводились экспериментальные исследования. Результаты теоретических расчетов и экспериментальных исследований приведены на рис. 2. Предложенная математическая модель зависимости акустической эффективности ВДПСТ может быть использована для теоретического определения акустической эффективности с величиной достоверности аппроксимации R2 = 0,93. Из представленных графических зависимостей следует, что характер изменения теоретических и экспериментальных кривых практически идентичен во всем рассматриваемом диапазоне частот (от 125 до 16000 Гц). Полученный результат подтверждает достоверность выдвинутой гипотезы и демонстрирует адекватность математической модели
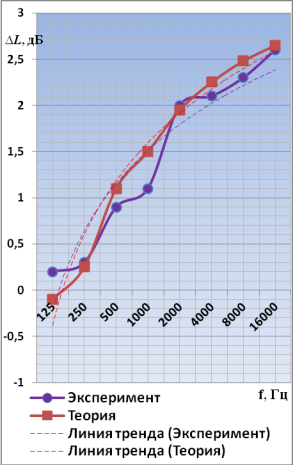
Рис. 2. Сравнительный анализ результатов теоретических исследований и натурных испытаний акустической эффективности ВДПСТ
Литература:
- Иванов Н. И. Основы виброакустики [Текст] / Н. И. Иванов, А. С. Никифоров. — СПб.: Политехника, 2000. — 482 с.
- Fesier W., Hauf, R. and Heuft.Noise measurement and hearing surveys in the woodworking industries // Applied Ergonomics. — 1971. — Vol. 2, Issue 4. — Р. 247.
- Reiter Jr. W.F., Keltie R. F.On the nature of idling noise of circular saw blades//Journal of Sound and Vibration. — 1976. –Vol. 44, — № 4,22 February 1976. — P. 531–543.
4. Martin Pohl, Michael Rose. Piezoelectric shunt damping of a circularsawblade with autonomous power supply fornoiseand vibration reduction // Journal of Sound and Vibration. — 2016. — Vol. 361, 20 January 2016. — P. 20–31.
- Осмоловский Д. С. Вибродемпфирующие свойства прокладок с сухим трением для снижения звуковой вибрации от круглопильных деревообрабатывающих станков [Текст] / Осмоловский Д. С., Асминин В. Ф.// Защита населения от повышенного шумового воздействия: Сборник докладов III Всероссийской научно-практической конференции с международным участием. Под редакцией Н. И. Иванова. Санкт-Петербург, 2011. — С. 652–658.
- Осмоловский Д. С. Экспериментальное исследование диссипативных свойств вибродемпфирующих прокладок с фрикционным трением для снижения шума от круглопильных деревообрабатывающих станков [Текст] / Д. С. Осмоловский, В. Ф. Асминин // Известия высших учебных заведений. Лесной журнал. — 2011. — № 5 (323). — С. 59–63.
