В современный образовательный процесс уже довольно глубоко укоренилось использование различных электронных дополнений с целью большего погружения в предмет. Одним из вариантов таких обучающих материалов являются модели тел и моделирование процессов, в основном, в тех ситуациях, когда воссоздать натуральную версию не представляется возможным. В технических и естественнонаучных предметах популярностью пользуются программы и приложения, дающие возможности интерактива.
Известный факт, что очень много людей запоминают меньше услышанного, чем увиденного. Если же информация будет идти в сопровождении звуковых и видеофрагментов, то запоминаемость материала повышается. Сейчас, благодаря интерактивным пособиям есть возможность представить информацию в различным формах, повышая эффективность учебного процесса. Визуализационный метод основан на одном из главных дидактических принципов — принципе наглядности. Впервые этот принцип применил Я. А. Коменский. Он сделал этот принцип частью как теоретических, так и практических занятий. Он считал, что наглядность является источником накопления знаний.
Преподавание технических и естественнонаучных предметов тяжело представить без наглядности. Главными «потребителями» являются, конечно, алгебра и геометрия. Формирование и развитие математических способностей учащихся основано на развитии наглядно-действенного, наглядно-образного, а в дальнейшем и абстрактного мышления. Сделать обучение более наглядным для учеников помогут учителю так называемые «интерактивные геометрические среды» (ИГС).
Почему в качестве среды разработки учебных материалов нами была выбрана GeoGebra? Данная среда свободно распространяется, т.н. программа с бесплатной лицензией и доступна для использования и учителям, и обучающимся всех уровней образования, при различных форматах проведения уроков и при различном техническом оснащении классов. Программное обеспечение включает в себя алгебраические и геометрические инструменты, различные таблицы, графы и элементы статистики.
Интерфейс программы напоминает учебную доску, на которой возможно разнообразные операции. Производимые изменения производятся в реальном времени: при изменении коэффициента в уравнении функции, график автоматически перестроится, при задании новых условий изменится масштаб и т. д.
Рис. 1. Интерфейс GeoGebra
Весь инструментарий можно комбинировать в одном проекте и даже на одном рабочем листе, давая возможность перейти от наблюдения к расчетам, а от них к решениям.
Возможности программы в области математики не ограничиваются лишь построением графиков, программа может быть использована для создания промежуточных интерактивных чертежей при решении задач из области геометрии. GeoGebra обладает мощным функционалом, который позволяет наглядно и просто обучаться.
Одним из важнейших инструментов является создание 3D-моделей. Одним из хороших примеров использования будет являться создание моделей в пространстве или в нестандартных разделах математики, таких как сферическая геометрия.
Сферическая геометрия — это раздел геометрии, изучающий тела на поверхности сферы. Прикладным применением является использование в географии, астрономии и других науках. Этот вид математики довольно тяжел для понимания и представления, поэтому интерактивные 3D-модели будут чрезвычайно полезны в обучении: возможность рассмотреть тело под любым углом, провести необходимые дополнительные построения и т. д.
Вы можете сделать конструкции точек, векторов, отрезков, прямых, многоугольников и конических сечений, а также функции и их динамические изменения. Он находит производные и интегралы от функций и предлагает такие команды, как Корень или Вершина.
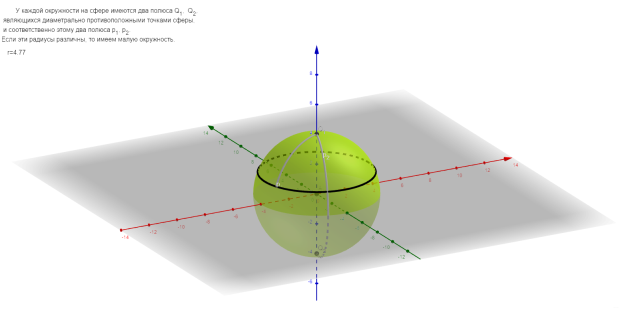
Рис. 2. Модель сферы
С помощью интерактивных моделей можно вникнуть в тонкости темы, провести необходимые измерения, разобраться с поставленной задачей или создать собственную. Данная программа позволяет создавать и редактировать модели без специальных знаний и навыков, имея только понимание изучаемого предмета.
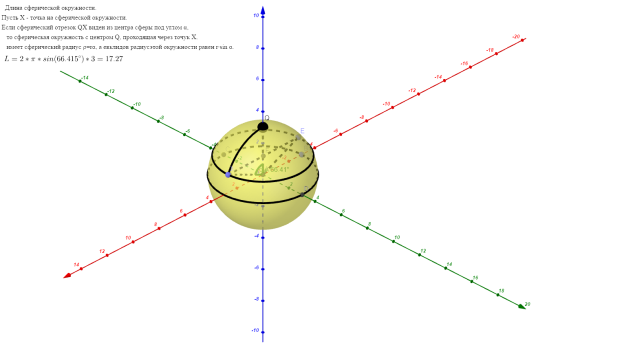
Рис. 3. Вычисление длины сферической окружности
Для работы на плоскости в качестве примера неплохо подойдет геометрия Лобачевского (гиперболическая геометрия), которая использует аксиомы Евклидовой геометрии, за исключением аксиомы о параллельности прямых.
Использование скриптов и дополнений позволяют выставлять дополнительные условия и еще больше дополнять функционал и рабочий материал.
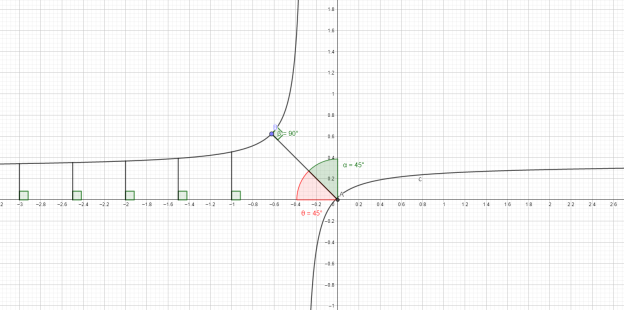
Рис. 4. Угол параллельности
В программе есть возможность скрывать необходимые объекты с помощью флажков. Заранее приготовив необходимый материал в проекте с помощью флажков, вы сможете скрывать или показывать изучаемый объект на уроке, демонстрируя разницу между моделями на практике. Также можно развивать творческие способности обучающихся, предлагая для их выполнение самостоятельные дополнительные задания,
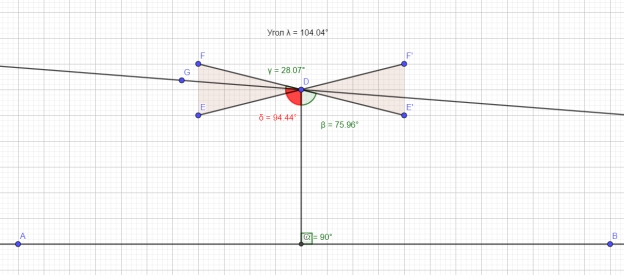
Рис. 5. Параллельные прямые в геометрии Лобачевского
Таким образом, программа «GeoGebra» — это хороший вариант для визуализации решений задач из разных областей математики и не только. С ее помощью можно повысить интерес к изучаемому предмету через интерактивность, наглядность и прозрачность процесса. А выполнение определенных заданий повысит уровень понимания темы среди обучающихся и поможет развить пространственное мышление.
Литература:
- Руководство — GeoGebra Manual // GeoGebra.org. URL: https://tinyurl.com/y3zmwher (дата обращения: 22.10.2019).
- Андрафанова Н. В. Интерактивная геометрическая среда как средство развития познавательного интереса школьников / Н. В. Андрафанова, Д. С. Назарян // Проблемы и перспективы развития образования в России. — 2014. — № 27. С. 59–65
- Markus Hohenwarter, Judith Hohenwarter Введение в GeoGebra версии 4.2. 2012. C. 153–154

