В настоящее время появилась возможность решения математических задач без составления компьютерных программ на языках программирования. Причиной этому является разработка специальных математических программ- математических систем. В научных исследованиях и в вузах на занятиях больше всего применяются следующие математические системы: MathCAD, MATLAB, Maple, Mathematika [1–3].При применении математических систем учебный процесс становится интересным, студенты понимают содержания занятия быстрее, глубоко, и для укрепления понятий и решения задач остаётся больше времени.
В статье возможности MathCAD демонстрируется в курсе «Численные методы» для приближённого решения задач алгебры и анализа. В MathCADе задачи решаются тремя способами:
1) с помощью стандартных внутренних функций MathCAD,
2) с помощью естественного математического алгоритма решения задачи,
3) с помощью математического алгоритма решения задачи, реализованного во внутреннем языке MathCAD. Мы рассмотрим в основном первые два способа.
Команды в MATHCADE записываются без всякого предопределителя и они не отличаются от математических формул с лишь следующей разницей: комбинация знаков двоеточие и равно (:=) означает определение, знак равно (=) или стрелка (→) означает вывод вычисленного значения. Кроме того, после нажатия знака «открывается площадка для ввода текста- замечания и по окончании ввода и нажатия клавиши Enter остаётся только текст-замечание. Мы в местах, где должно быть текст-замечание записываем знак «и, после него, вводим текст-замечание. Это облегчает понимание алгоритма решения.
1. Приближённое решение одного нелинейного уравнения.
В MathCADе для приближённого решения одного уравнения имеются внутренные стандартные функции: 1)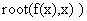 
, given..find — для произвольных уравнений 
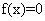, 2)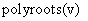 
-для полиномиального уравнения 
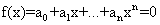, здесь 
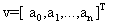— вектор коэффицентов. Коэффициенты вводятся именно в таком порядке.
Пример 1. Решить уравнение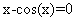 
.
Записываем в MATHCADе следующие команды:
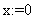
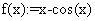«начальная итерация и уравнение
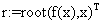
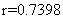«ссылка к внутренней функции и вывод решения.
Пример 2. Определение всех решений уравнения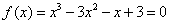
.
Решение:
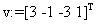
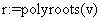
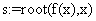«внутренние функции
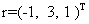
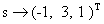«вывод решения
Организуем теперь алгоритмы методов простой итерации ва Ньютона, они имеют важное значение при изучении методов.
Пример 3. Метод итерации. Решим уравнение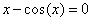 
. Решение:
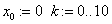«задание начальную итерацию ва их количества
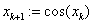«приведение 
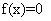к виду 
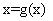и построение итераций
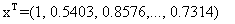«вывод результата
Пример 4.Метод Ньютона. Рассмотрим опять уравнение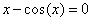. Решение:
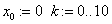«задание начальную итерацию ва их количества
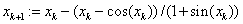«метод Ньютона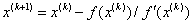 
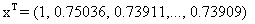«вывод результата
2. Приближённое решение систем нелинейных уравнений.
В MathCADе имеются стандартные функции для приближённого решения систем нелинейных уравнений: блок given..find, внутренние функции minimize (f(x),x), minerr(x).
В качестве примера рассмотрим систему нелинейных уравнений:
, 
.
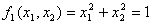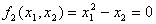1) использование блока given..find.
Решение:
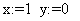«задание начальную итерацию
Given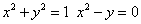 
«задание системы, равенство жирное
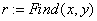«присвоение решения переменной
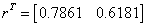«вывод корней
При начальной итерации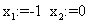 
получаем решение 
.
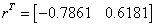2) Метод минимизации. Вышеприведённую систему сведём к задачу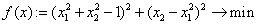 
.
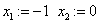«задание начальную итерацию (
)
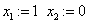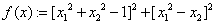«целевая функция
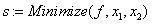«обращение к внутренней функции
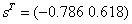«вывод решения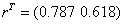 
При начальной итерации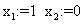 
получаем решение .
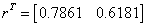3) Использование внутренней функции minerr(x)
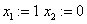«задание начальную итерацию
Given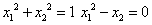 
«задание системы, равенство жирное
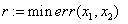«обращение к внутренней функции
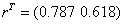«вывод решения
4) Метод итерации. Рассмотрим систему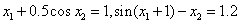 
.
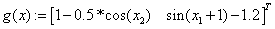«задание итерационых функций,
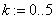
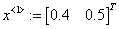«задание числа итераций и начальную итерацию
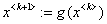«построение итераций
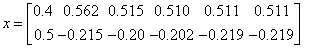«вывод последовательности итераций
При начальной итерации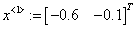 
получаем решение
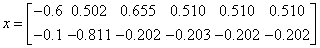«решение
5) Организация метод итераций Ньютона: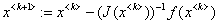 
.
ORIGIN:=1 «установка начального индекса
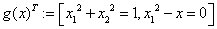«задание уравнения
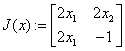
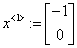«матрица Якоби и начальная итерация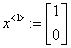 
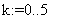
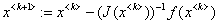«итерации Ньютона
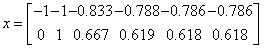«итерации для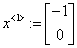
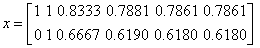«итерации для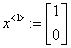
Формулу 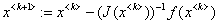пока удалось реализовать только в MathCADе.
3. Решение задач алгебры. В MathCADе очень многие задачи алгебры решаются достаточно наглядно и этот процесс проводиться в естественном математическом языке. Процесс решения настолько простой, и мы ограничимся демонстраций некоторых основных внутренних функций. Имеем
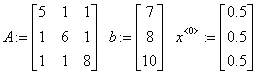«матрица, правая часть, начальная итерация
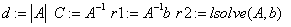«детерминант, обратная матрица, корни
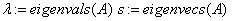«собственные значения и векторы
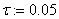
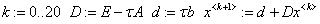«построение итераций
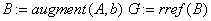«расширенная и ступенчатая матрица
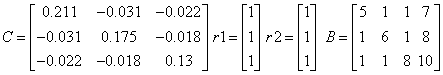«результаты
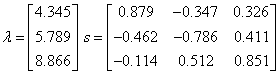
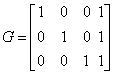
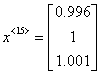«результаты
Здесь B расширенная матрица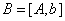 
, G-ленточный вид матрицы В после применения метода Гаусса, 
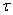-итерационный параметр, 
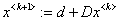-метод итерации, lsolve (решение 
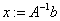) augment, rref, eigenvals (собственные значения), eigenvecs (собственные векторы)-внутренние функции MathCAD.
4. Построение интерполяция формул. Пусть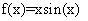 
.
А) Интерполируем f(x) многочленом Лагранжа 4-ой степени. Наберём в окне MathCADе следующие команды:
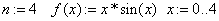«количество точек, функция, отрезок
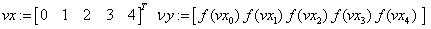«узлы, значения 
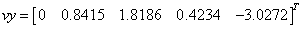«вывод значения функции
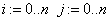
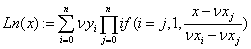«многочлен Лагранжа
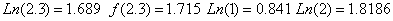«значения многочлена.
Б) Интерполируем f(x) многочленом Ньютона 4-ой степени. Наберём в окне MathCADе следующие команды:
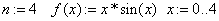«количество точек, функция, отрезок
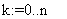
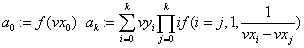«разделённые разности
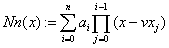
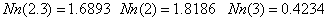«результаты
5. Построение квадратурных формул. Интеграл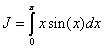 
вычислим квадратурными формулами прямоугольников, трапеций, Симпсона и Гаусса.
Записываем следующие команды в MathCADe:
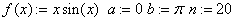«функция, отрезок, количество точек
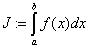
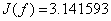«интеграл
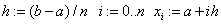«шаг, узлы
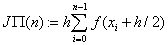
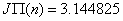«формула прямоугольников
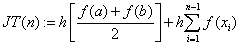
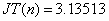«формула трапеций
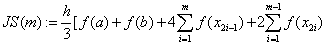«формула Симпсона
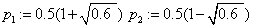«коэффициенты формулы Гаусса
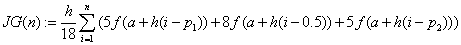«формула Гаусса
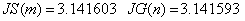«приближённые значения интеграла
6. Задача Коши для обыкновенного дифференциального уравнения
Решим приближённо задачу Коши для ОДУ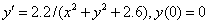 
методами Рунге-Кутта. Записываем следующие команды в MathCAD:
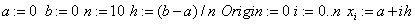«отрезок, узлы
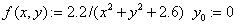«ОДУ правая часть, начальное условие
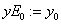
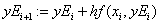«метод Эйлера
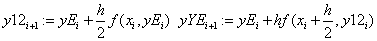«совершенный метод Эйлера
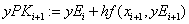«метод прогноза коррекции
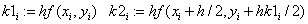«коэффициенты метода РК
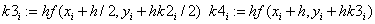«коэффициенты метода РК
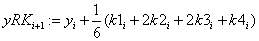«формула Рунге-Кутта
Производя вычисления, получим следующую таблицу значений решения:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
yE |
0 |
0,846 |
1,356 |
1,617 |
1,771 |
1,873 |
1,943 |
1,995 |
2,035 |
2,066 |
|
yYE |
0 |
0,772 |
1,284 |
1,575 |
1,746 |
1,857 |
1,933 |
1,989 |
2,03 |
2,063 |
|
yPK |
0 |
0,51 |
1,107 |
1,511 |
1,718 |
1,842 |
1,925 |
1,983 |
2,026 |
2,06 |
|
yRK |
0 |
0,539 |
1,077 |
1,466 |
1,681 |
1,814 |
1,903 |
1,966 |
2,013 |
2,049 |
Все методы, внутренние функции дают достаточно хорошее приближение к решению. В этом мы убедились, решая одну задачу несколькими методами или решая задачи, с известными точными решениями.
Литература:
1. Алексеев Е. Р., Чеснокова О. В. Решение задач вычислительной математики в пакетах MathCAD, MATLAB, Maple 9. –М.:НТ Пресс, 2006.-496 с.
2. Имомов А. Численные методы и MathCAD. Наманган, НамГУ, Учебно-методическое пособие. 2012 г.-96 с.-znuz_215446_20120119115351.rar.
3. Имомов А. Организация решения дифференциальных уравнений в MathCADе. Усовершенствования преподавания физики, математики и информатики в академических лицеях и коллежах. Материалы 7-традиционной республиканской научно-практической конференции вузов. 1-часть. Ташкент, 2011.-38–41 с.
4. Поршнев С. В., Беленкова И. В. Численные методы на базе MathCAD. СПб, 2005.-464 с.
5. Ракитин В. И. Руководство по ВМ и приложения MathCAD. М.:ФМ, 2005.-264 с.
6. Охорзин В. А. Прикладная математика в системе MathCAD. СПб, Лань,2008–352 с.
7. С. С. Ирискулов, К. Д. Исманова, М.Олимов, А.Имомов. Численные методы и алгоритмы. MathCAD. Учебное пособие. Изд-во “Наманган”, Наманган, 2013.-276 с.
