Принципы распараллеливания. Для многих методов матричных вычислений характерным является повторение одних и тех же вычислительных действий для разных элементов матриц. Данное свойство свидетельствует о наличии параллелизма по данным при выполнении матричных расчетов, и, как результат, распараллеливание матричных операций сводится в большинстве случаев к разделению обрабатываемых матриц между процессорами используемой вычислительной системы. Выбор способа разделения матриц приводит к определению конкретного метода параллельных вычислений; существование разных схем распределения данных порождает целый ряд параллельных алгоритмов матричных вычислений.

Наиболее общие и широко используемые способы разделения матриц состоят в разбиении данных на полосы (по вертикали или горизонтали) или на прямоугольные фрагменты (блоки).

Вектор средства векторной обработки, помещенные в виде одномерного массива хранения данных на регулярной основе (как правило, в форме запятой) коренных пород, что есть. Если, при обработке многомерного массива, они должны рассматриваться как вектор. Принимая во внимание безопасность многомерного массива в памяти, такой подход может быть.

1. Ленточное разбиение матрицы. При ленточном (block-striped) разбиении каждому процессору выделяется то или иное подмножество строк (rowwise или горизонтальное разбиение) или столбцов (columnwise или вертикальное разбиение) матрицы (рис. 1). Разделение строк и столбцов на полосы в большинстве случаев происходит на непрерывной (последовательной) основе. При таком подходе для горизонтального разбиения по строкам, например, матрица A представляется в виде (см.рис.1)

Рис. 1. Способы распределения элементов матрицы между процессорами вычислительной системы

A=(A₀,A₁,…….,A_p-1)^T, A_i=(a_i0,a_i1,……,a_ik-1), i_j=ik+j, 0 ≤ j <k, k="m/p,</em"></k,>

Где a_i=(a_i1,a_i2,...,a_in),0i<m, (предполагается,="" <="" a="" i-я="" m="k·p)." p="" p,="" алгоритмах="" будут="" в="" вектор,="" во="" всех="" данных="" есть="" и="" количество="" которые="" кратно="" лекциях,="" матрицы="" матричного="" на="" непрерывной="" основе.="" применяется="" процессоров="" разделение="" рассмотрены="" следующей="" строк="" строка="" т.е.="" умножения="" числу="" что="" этой="">

Другой возможный подход к формированию полос состоит в применении той или иной схемы чередования (цикличности) строк или столбцов. Как правило, для чередования используется число процессоров p – в этом случае при горизонтальном разбиении матрица A принимает вид

A=(A₀,A₁,…….,A_p-1)^T, A_i=(a_i0,a_i1,……,a_ik-1), i_j=i+jp, 0 ≤ j <k, k="m/p,</em"></k,>

Циклическая схема формирования полос может оказаться полезной для лучшей балансировки вычислительной нагрузки процессоров (например, при решении системы линейных уравнений с использованием метода Гаусса).

2. Блочное разбиение матрицы. При блочном (chessboardblock) разделении матрица делится на прямоугольные наборы элементов – при этом, как правило, используется разделение на непрерывной основе. Пусть количество процессоров составляет p=s·q, количество строк матрицы является кратным s, а количество столбцов – кратным q, то есть m=k·s и n=l·q. Представим исходную матрицу A в виде набора прямоугольных блоков следующим образом:

,

гдеA_ij — блок матрицы, состоящий из элементов:

,

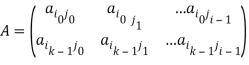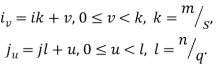
При таком подходе целесообразно, чтобы вычислительная система имела физическую или, по крайней мере, логическую топологию процессорной решетки из s строк и q столбцов. В этом случае при разделении данных на непрерывной основе процессоры, соседние в структуре решетки, обрабатывают смежные блоки исходной матрицы. Следует отметить, однако, что и для блочной схемы может быть применено циклическое чередование строк и столбцов.

Рассматриваются три параллельных алгоритма для умножения квадратной матрицы на вектор. Каждый подход основан на разном типе распределения исходных данных (элементов матрицы и вектора) между процессорами. Разделение данных меняет схему взаимодействия процессоров, поэтому каждый из представленных методов существенным образом отличается от двух остальных.

Классификация архитектур параллельной обработки

В 1966 году М.Флинном был предложен подход к классификации архитектур вычислительных систем. В основу было положено понятие потока, под которым понимается последовательность элементов, команд или данных, обрабатываемая процессором. Соответствующая система классификации основана на рассмотрении числа потоков инструкций и потоков данных.

Классификация Флинна [79, 80] является одной из первых и наиболее известных классификаций архитектур вычислительных систем. Данная классификация базируется на понятии потока, под которым понимается последовательность элементов, команд или данных, обрабатываемая процессором. Каждый поток не зависит от других потоков, и каждый элемент потока может состоять из нескольких команд или данных. На основе числа потоков команд и потоков данных Флинн выделяет четыре класса архитектур: SISD, MISD, SIMD, MIMD.

Таблица 1

Классификация Флинна

SISD: последовательные ЭВМ. SIMD: ЭВМ с конвейерной, функциональной или матричной параллельной обработкой данных. MISD: ничего известного науке. MIMD: ЭВМ с мультипроцессорной обработкой данных. Классификация Флинна самая простая, распространенная и бесполезная: параллельные ЭВМ фактически делятся на два класса, причем большинство современных ЭВМ могут быть отнесены и к тому и к другому. Пример: ЭВМ с векторно-конвейерной архитектурой процессора есть в однопроцессорном (SIMD) и в многопроцессорном (MIMD) исполнении.

Литература:

1. Каримов И.А. Мировой финансово-экономический кризис, пути и меры по его преодолению в условиях Узбекистана. – Т.: Узбекистан, 2009. – 31 с.
2. Каримов И.А. Узбекский народ никогда и ни от кого не будет зависеть. Т.13. – Т.: «Узбекистан», 2005. – 264 с.
3. ADSP-BF533 Blackfin Booting Process (EE-240) Rev 3.0, January 2005. AnalogDevices, Inc.
4. Бартенев В.Г., Бартенев М.В. Анализ эффективности многоканальной системы с адаптивным порогом на модуле ЦОС STAMP. Цифровая обработка сигналов.