В настоящее время большое значение имеет решение прикладных задач, что дает толчок к развитию различных отраслей науки.
Значительная часть прикладных задач связана с методами оптимизации. Оптимизация применяется с различной целью, в зависимости от той цели, которую поставила данная отрасль. На рисунке 1 представлены статистические данные профессионального сообщества IT-директоров России Global CIO [3].
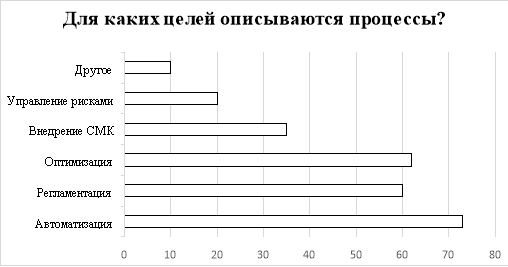
Рис. 1. Результаты опроса партнеров Global CIO, для каких целей они описывают процессы внутри компании
Из вышесказанного следует, что главными целями при этом остаются автоматизация процессов, их регламентация и стандартизация, а также оптимизация.
Главным достоинством существующих методов нахождения экстремумов является простота и нахождение глобальных максимумов и минимумов, однако, в ряде поставленных задач исследования временных рядов, было необходимо произвести большой объем вычислений с минимальными временными и вычислительными затратами, что большинство существующих методов не позволяет реализовать.
Целью исследования является повышение точности прогноза заданного временного ряда на основе модели полигармонического полинома.
Для достижения поставленной цели в работе поставлены следующие задачи:
1 Нахождение промежутков возрастания и убывания числовой последовательности {M}Ni=1
Пусть существует числовая последовательность {M}Ni=1 длиной N состоящий из чисел x, принадлежащих множеству рациональных чисел Q.
] ∃ {M}Ni=1, где x ∈ M и x ∈ {Q}
Так как любой числовой ряд можно представить композицией гармонических функций то будем считать, что {M}Ni=1 является функцией представленной в виде полигармонического полинома.
1) Пусть x(i) это число функции M(N) где i это номер числа x в ряду M(N), а x(i+1) следующее число последовательности {M}Ni=1
2) Пусть область допустимых значений функции от 0 до ![]()
![]()
Пусть область определения функции от 0 до ![]()
![]()
3) Тогда функция {M}Ni=1 возрастает там где f `(x(i)) > 0 и убывает там где f `(x(i)) < 0 при том что {M}Ni=1 определена и непрерывна на всей E(М)
4) Найдем все промежутки возрастания и убывания {M}Ni=1 начиная с первого элемента функции.
Пусть m это начала промежутка функции, k это конец промежутка, тогда: {M}Ni=1 убывает на интервале от (m; k) если f `(x(i)) < 0 при x(i) ![]() (m; k)
(m; k)
Определение интервалов при убывании функции:
m = i
Если: f `(x(i)) < 0
i = i + 1
Если f `(x(i)) > 0
k = i — 1
{M}Ni=1 возрастает на интервале от (m; k) если f `(x(i)) > 0 при x(i) ![]() (m; k)
(m; k)
Определение интервалов при возрастании функции:
m = i
Если: f `(x(i)) > 0
i = i + 1
Если f `(x(i)) < 0
k = i — 1
2 Нахождение минимума числовой последовательности на интервале N
Пусть существует числовая последовательность {M}Ni=1 длиной N состоящий из чисел x, принадлежащих множеству рациональных чисел Q.
] ∃ {M}Ni=1 где x ∈ M и x ∈ {Q}
2) Пусть x(i) это число ряда M(N) где i это номер числа x в ряду M(N), а x(i+1) следующее число последовательности {M}Ni=1
3) Вычислим шаг суммирования q как производную от x(i)
q = -f `(x(i))
4) Обозначим критерий С = 0,5 которая будет являться пороговым значением при нахождении локального минимума числовой последовательности
5) Вычислим x(i+1) как сумму шага суммирования и значение точки x(i)
x(i + 1) = x(i) + q
6) Обозначим систему условий нахождения локального минимума x(min) последовательности {M}Ni=1
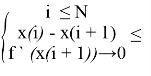 C
C
Тогда:
X(min) = x(i + 1) если 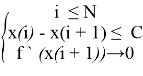
3 Нахождение максимума числовой последовательности на интервале N
Пусть существует числовая последовательность {M}Ni=1 длиной N состоящий из чисел x, принадлежащих множеству рациональных чисел Q.
] ∃ {M}Ni=1 где x ∈ M и x ∈ {Q}
1) Пусть x(i) это число ряда M(N) где i это номер числа x в ряду M(N), а x(i+1) следующее число последовательности {M}Ni=1
2) Вычислим шаг суммирования q как производную от x(i)
q = f `(x(i))
3) Обозначим критерий С = 0,5 которая будет являться пороговым значением при нахождении локального минимума числовой последовательности
4) Вычислим x(i+1) как сумму шага суммирования и значение точки x(i)
x(i + 1) = x(i) + q
4) Обозначим систему условий нахождения локального минимума x(min) последовательности {M}Ni=1
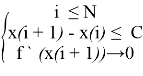
Тогда:
X(max) = x(i + 1) если 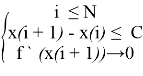
В работе был рассмотрен метод нахождения точек экстремума спектральной области временного ряда для определения уточнения гармоник модели полигармонического полинома. Достоинством рассмотренного метода является простота алгоритмизации, минимальные временные и вычислительные затраты. Данный метод повышает точность прогнозного ряда путем нахождения максимальных значений гармоник временного ряда в спектральной области.
Литература:
1 Аралбаев Т. З. Построение адаптивных систем мониторинга и диагностирования сложных промышленных объектов на основе принципов самоорганизации; Уфа: Гилем, 2003. — 247 с.: ил.;
2 Тенденции и комментарии [Электронный ресурс] / Интернет– ресурс. — Режим доступа к статье: http://dit.isuct.ru/IVT/sitanov/Literatura/M171/Pages/Glava1_1.htm
3 Методы одномерной оптимизации [Электронный ресурс] / Интернет– ресурс. — Режим доступа к статье: http://dit.isuct.ru/IVT/sitanov/Literatura/M171/Pages/Glava1_1.htm







