Анализ и предварительная обработка данных для решения задач прогнозирования в сфере услуг здравоохранения



Система здравоохранения — важный социальный институт, который является совокупностью организаций, ресурсов и учреждений, направленных на оказание медицинской помощи. Такая система основана на трех базовых принципах: лечение заболеваний, поддержание здоровья населения и оказание финансовой поддержки в оплате медицинских услуг. Для качественного выполнения функций системы здравоохранения, необходима слаженная работа всех ее компонентов: финансового отдела, компетентных работников, руководства, а также аппарата всеобщего управления. Основной целью такой системы является повышение качества жизни населения за счет оказания услуг, чутко реагирующих на запросы граждан и справедливых с финансовой точки зрения. Важность слаженной работы этого механизма и всех его структур неоспорима так, как это оказывает влияние на качество оказываемых услуг.

Планирование и прогнозирование бюджета больницы сказывается на ее развитие так, как качество предоставляемых населению услуг коррелирует с возвратом затрат на их оказание. Возмещение медицинским учреждениям затрат на лечение граждан РФ оказывают страховые медицинские организации (СМО).

В настоящее время в больницах идет активное внедрение информационных технологий. Однако система работы финансового отдела учреждения здравоохранения требует оптимизации и уменьшения влияния на точность работы человеческого фактора.

Медицинские учреждения обладают массивными базами данных, в которых хранится много информации. Ее анализ мог бы помочь во многих процессах принятия решений. Примерами таких процессов являются: прогнозирование бюджета больницы, предсказывание загруженности стационарных подразделений, оптимизация закупок лекарств в зависимости от потребностей населения. Но, к сожалению, на данным момент эта информация никак не анализируется, хотя могла бы оптимизировать многие процессы.

В данной статье мы рассмотрим этапы предварительной обработки для дальнейшего моделирования полученных выборок. А также проведем анализ данных и расскажем, как понимание взаимосвязи данных влияет на выбор методов предварительной обработки. Применение выбранных методов будет приведено на примере оптимизации процесса распределения и предсказания бюджета внутри больницы между страховыми медицинскими организациями.

В начале каждого месяца, который равен одному отчетному периоду, сотрудники учреждения строят прогноз, указывающий на какую сумму они окажут услуги в текущий период. В течение месяца этот прогноз может быть изменен, но все поправки сопровождаются документооборотом и проходят через множество структур до полного их утверждения. Это занимает некоторое время, на практике оказывается, что после первой половины месяца, процедура внесения правок не успевает закончиться, до нового периода. После установления суммы, на которую медицинское учреждение окажет услуги пациентам, эти данные отправляются в СМО, которое компенсирует затраты на лечение.

Определение объемов на будущий месяц оказанной медицинской помощи застрахованным лицам напрямую влияет на дальнейшее финансирование учреждения. В случае превышения суммы, на которую оказали услуги, в сравнении с изначальным прогнозом, СМО не возмещает затраты за допущенную погрешность. В обратном случае, это оказывает влияние на дальнейшее финансирование учреждение и объем бюджета на следующий год.

В настоящий момент основным методом решения выявленной проблемы является интуитивный подход к построению прогноза. Суть подхода основывается на логическом анализе финансовой ситуации, состоянии здоровья населения и опыте финансового отдела.

Эксперт должен провести самостоятельную работу над оценкой тенденций прогнозируемого объекта, его состояний и вариантов развития, а также погрешностей, допущенных в предшествующие года на основе опыта. Как результат получается, что точность прогноза зависит от компетентности и внимательности каждого специалиста. Прямая зависимость от человеческого фактора влечет за собой неточные оценки, а вследствие этого появляется большая погрешность при построении прогноза. Стоит отметить отрицательный момент данного подхода в том, что при смене сотрудника, опыт полученный за предыдущие года теряется.

Неточно планирование влечет за собой проблемы в финансировании. Но один из худших исходов, которые могут повлечь за собой ошибки при построении прогноза, это закрытие учреждения.

На текущий момент не разработано программы, способной решить поставленную задачу в полной мере. Наиболее популярны и широко распространены программы, которые предсказывают продажи определенного товара, либо планируют стратегию складов предприятий. Есть отдельные инструменты, которые в комплексе могут спрогнозировать бюджет учреждения, но для этого весь процесс должен осуществлять компетентный специалист.

На рынке существуют коммерческие продукты предоставляющие инструменты для анализа данных и прогнозирования, лицензия на которые требует больших затрат. К тому же дорогостоящие программы с нужным функционалом не адаптированы под российскую систему финансирования больниц. Также схожим функционалом обладает Excel, но и он требует специалиста, обладающего фундаментальными знаниями математической статистики.

Для реализации всех методов был использован язык python так, как он использовался для написания всех систем, разработанных заказчиком, и в дальнейшем для упрощения интегрирования разработанной программы. Python — это высокоуровневый интерпретируемый язык, имеющий простой синтаксис и экономящий время разработчика, что ведет к повышению производительности на практике. Он обладает большим функционалом и применим для широкого круга задач. Для математической статистики и моделирования существуют многофункциональные библиотеки, включающие в себя множество тестов, моделей, и способные с помощью визуального представления помогать в интерпретации данных.

Моделирования данных и построения графиков использовалась библиотека Matplotlib. Она позволяет получать визуальное представление данных в различных форматах в печатном виде и в интерактивных средах на разных платформах. С её помощью можно построить графики, гистограммы, спектры мощности, диаграммы ошибок и разброса, используя всего несколько строк кода.

Для анализа и предварительной обработки данных помимо стандартных функций языка python использовалась библиотека statsmodels, предоставляющая классы и функции для оценки различных статистических моделей, а также для проведения тестов и анализа статистических данных. Помимо этого все результаты тестов проверяются с помощью встроенных пакетов, чтобы убедиться в их правильности.

Но самой базовой библиотекой при математическом моделировании является pandas. Это пакет Python, обеспечивающий быстрые, гибкие и выразительные структуры данных, предназначенные для того, чтобы сделать работу с реляционными данными простой и интуитивно понятной. Разработчики позиционируют его как фундаментальный блок высокого уровня для практического анализа данных в Python.

Scikit-learn это еще одна библиотека, но основной её функционал направлен на реализацию алгоритмов машинного обучения. Но также она имеет различные алгоритмы классификации, регрессии и кластеризации, включая векторные вычисления, градиент, k — средних, и интегрирована с численными и научными библиотеками NumPy и SciPy.

В качестве инструментов разработки использовалась сборка Anaconda, которая включает в себя:

– установленный Python 2.7, 3.4, 3.6

– порядка 300 готовых к установке библиотек и около 150 уже предустановленных (включая все вышеописанные библиотеки)

– установленный IDLE Spider 2

В качестве исходных данных была предоставлена массивная база данных медицинской информационной системы, которую используют медицинские учреждения на территории Краснодарского края с 2013 года. Предоставленные данные оказались избыточны так, как база данных содержала сотни таблиц с информацией о пациентах, работниках, технике, ресурсах и справочной информации. Для решения задачи нужно определить принадлежность данных и составить информативную выборку, для оптимизации процесса принятия решений.

Проанализировав предметную область, можно сделать формальный вывод, что для решения поставленной задачи необходимы уникальные знания о каждом визите застрахованного лица в учреждение и издержки предоставленных услуг. Для их идентификации и избежания дублирования в указанной системе выборка определяется по уникальному номеру события. А также затраты на каждую предоставленную услугу, можно вычислить основываясь на таблице, содержащей перечень услуг и их стоимость, описывающийся тарифным соглашением в сфере обязательных медицинского страхования по Краснодарскому краю.

Всю вышеперечисленную информацию нужно агрегировать по дням, после этого сформировать выборку и записать в csv файл. Для дальнейшего анализа необходимо посмотреть на получившиеся данные. Для этого построим график, где ось задают дни недели, ось сумму, на которую пациентам оказали услуги в данный день.

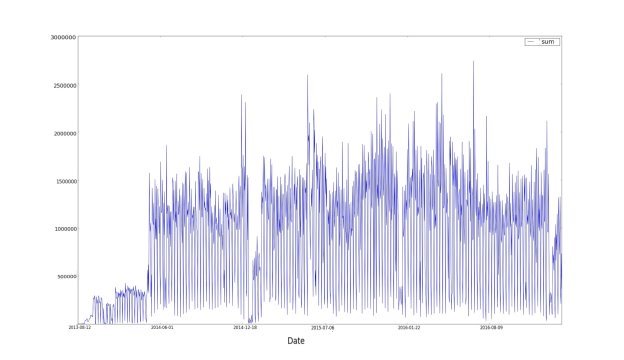
Рис. 1. Исходные данные

Как видно из рисунка 1, полученные данные оказались грязными, то есть обладающими низким качеством. Процесс предварительной обработки данных до начала анализа необходим для приведения их к соответствующим требованиям, задаваемым предметной областью. В указанной процедуре можно выделить два этапа: очистку, необходимую для повышения качества данных, и оптимизацию, выявление и исключение незначащих признаков.

Очистка направлена на устранение ошибок в данных с тем, чтобы эти данные адекватно и последовательно представляли процесс, в результате которого они были получены.

Первым этапом очистки данных является устранение противоречий и дубликатов. С первым в решаемой задаче нет нареканий. Все данные логичны и не противоречат друг другу и на уровне описательной характеристики показателей, и на уровне представления их в базе данных. А проблема с дубликатами решаются грамотно разработанной системой, не допускающей повторение данных с помощью уникального номера, присваиваемого каждому визиту и пациенту.

Следующим этапом в процессе подготовки данных будет восстановление целостности. Специалисты предметной области не смогли объяснить почему в данных имеются пропуски, то есть даты в которые полностью отсутствует информация о посещениях. Очевидно это является недостоверной информацией, т. к. с минимальной вероятностью возможно, чтобы во всей области не было ни одного обратившегося человека. Поэтому целостность данных была восстановлена путем добавления недостающих дат, а на месте значений записаны нули. Такой подход не скажется отрицательно на результате, обоснование этому приводиться дальше.

В результате качество данных было повышено, что приведет к эффективной работе модели и достоверности результатов анализа. Но данные по-прежнему являются избыточными и обладающими выбросами, поэтому следует провести оптимизацию данных.

Оптимизация данных необходима для избавления от несущественных значений и адекватной работы модели. Следствием неудачной оптимизации могут служить неточные результаты предсказания в дальнейшем, невозможность извлечь нужные выборки.

Для начала следует объяснить маленькие значения относительно всей выборки в начале 2013 года. Объяснение этому дали специалисты, занимающиеся медицинской информационной системой. Процесс перехода на новый вид отчетности и ведения базы данных происходил постепенно, что повлекло за собой увеличение числа учреждений, а значит и числа пациентов. Из этого следует, что для правдоподобности выборки, следует рассматривать более стабильный участок. Поэтому будем вести отсчет с начала 2014 года.

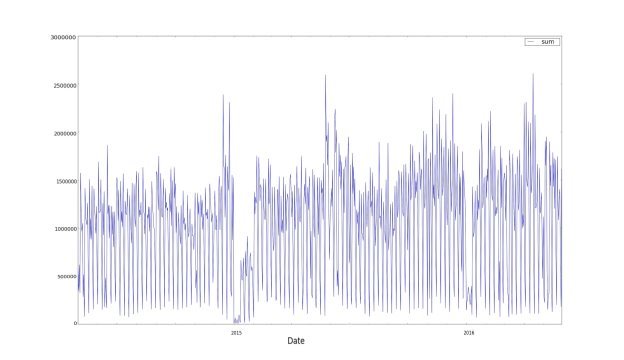
Рис. 2. Стабильная выборка данных

Перед тем, как приступить к выбору метода прогнозирования, необходимо оценить, что из себя представляют данные. Количественное прогнозирование может применяться, когда выполнены два условия:

1. Имеется информация о прошлом
2. Некоторые аспекты прошлых результатов будут продолжаться и в будущем

Существует широкий диапазон количественных методов прогнозирования, часто разрабатываемых в конкретных дисциплинах для конкретных целей. Каждый метод имеет свои свойства, точность и затраты, которые необходимо учитывать при выборе конкретного метода. В большинстве проблем количественного прогнозирования используются либо данные временных рядов (собираемые через регулярные интервалы времени), либо данные поперечного сечения (собранные в один момент времени).

С данными поперечного сечения мы хотим предсказать ценность чего-то, чего мы не наблюдали, используя информацию о случаях, которые мы наблюдали. Данный подход к прогнозированию не подходит для рассматриваемой задаче.

Данные временных рядов полезны, когда предсказываются наблюдения, которые со временем меняются, например: ежедневные цены на акции Mail.ru, ежемесячные осадки, квартальные результаты продаж для Avito, годовая прибыль Яндекс. Все, что наблюдается последовательно во времени, представляет собой временной ряд.

При прогнозировании данных временных рядов, производится оценка, как последовательность наблюдений будет продолжаться в дальнейшем. Такой ряд состоит из двух элементов: отметках во времени и замерах (значениях), соответствующим указанной отметки времени. С полной уверенностью можно сказать, что мы работаем с временным рядом.

Главной характеристикой временных рядов является их стационарность. Именно эта характеристика в дальнейшем определяет методы, которые применимы к задаче, и этапы дальнейшей работы. Из рисунка 2 видно, что во временном ряде присутствует шум, перед дальнейшим исследованием на стационарность его следует сгладить.

Как видно из графика он обладает большими выбросами, что неблагоприятно скажется на адекватности работы модели. Более детально изучив спады, исходя из предметной области, их можно объяснить человеческим фактором. А именно, каждый спад совпадает с выходными, соответственно учреждения здравоохранения не ведут общий прием в эти дни, а также резкие подъемы выпадают на понедельники, из чего следует предположение, что работники не своевременно заносят данные в информационную систему. Так как повлиять на своевременность ввода данных невозможно, их необходимо сгладить.

Методы сглаживания помогают выделить тренд — повторяющуюся часть временного ряда. При применении метода следует заранее вычислить период, если он существует. В конкретной задаче, вследствие того, что информационная система заполнялась несвоевременно, и существует необходимость перераспределения значений, был выбран метод экспоненциального сглаживания.

Для сглаживания ряда с помощью выбранного метода необходимо рассчитать экспоненциальные скользящие средние. Идея метода заключается в том, что экспоненциальная средняя рассматривается как асимметричная взвешенная скользящая средняя, в которой предшествующие данные берутся с разными коэффициентами, значения весов коэффициентов убывают по экспоненте в зависимости от удаления от текущей точки.

Пусть есть временной ряд, тогда суть метода описывается в виде рекуррентного выражения:

,

где: — сглаженный ряд, — значение в момент t, — есть коэффициент сглаживания.

От определения значения коэффициента зависит насколько предшествующие данные будут оказывать влияние на текущее. Для выбора наиболее оптимального метода вычисления значения нет. Но есть общий принцип, если начальные условия являются достоверными, следует минимизировать значение , если же есть сомнения в их достоверности, то следует выбирать большую величину , что приведет к большему влиянию последних значений на сглаживаемую точку.

На практике при выборе малого, дисперсия в большей степени сокращается, тем самым подавляя колебания изначального ряда, а в случае больших значений разброс незначительно отличается от дисперсии ряда .

Для реализации метода экспоненциального сглаживания, в языке python существует функция DataFrame.ewm(). Один из параметров функции задает значение коэффициента . Для выбора коэффициента стоит исходить из предметной области, т. к. на рис.1 можно заметить повторяющийся период равный неделе, то предположим, что =7. Применив сглаживание с указанным параметром, получаем более гладкий ряд относительно исходного:

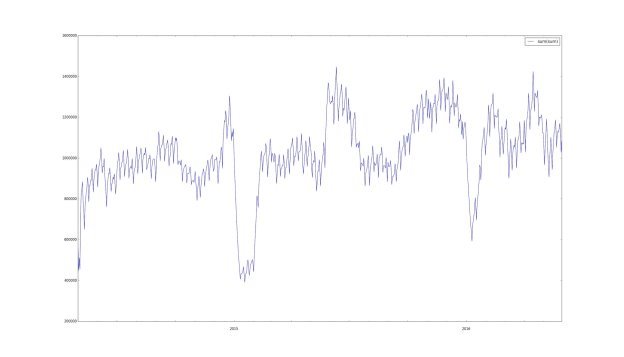
Рис. 3. Сглаженный ряд

Можно заметить, что новый временной ряд, при выбранном коэффициенте, не имеет больших выбросов и возможно имеет тренд. Так как спады в начале каждого года можно объяснить новогодними праздниками. Исходя из формального определения временного ряда можно сделать предположение, что ряд нестационарный. Для проверки этого утверждения построим на гистограмму и рассмотрим характеристики ряда.

Для оценки однородности временного ряда и характера разброса его значений, стоит прибегнуть к описательной статистики. Временной ряд необходимо охарактеризовать с точки зрения статистики удобно интерпретируемыми показателями. К таким показателям можно отнести: число элементов выборки, среднее значение, минимальное и максимальное значения, стандартное отклонение, квартили. С помощью показателей можно оценить характер выбросов. Построим для этого гистограмму распределения значений:

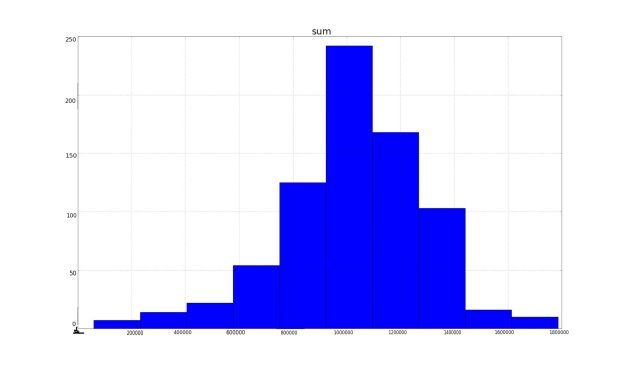
Рис. 4. Гистограмма распределения значений

Как можно заметить из гистограммы на рисунке 4, получившийся ряд имеет относительно исходного небольшой разброс и однородность. Для более точной оценки следует вычислить коэффициент вариации, который в процентном соотношении относительно среднего показывает однородность разброса значений.

Пусть — среднеквадратическое отклонение и — среднее арифметическое выборки, вычисляются по формулам:

, ,

где — значение статистического ряда, n — количество значений в ряду. Тогда коэффициент вариации вычисляется по формуле:

Если в результате коэффициент получается равным 0 %, то ряд является абсолютно однородным. Если он будет больше 33 %, то относительно среднего значения происходит большой разброс, и ряд является неоднородным.

Для вычисления коэффициента нам необходимы основные стандартные характеристики ряда. В библиотеке pandas существует стандартная функция describe(), которая предоставляет результаты таких показателей как: количество элементов выборки, медиана, среднеквадратическое отклонение, минимум, максимум и процентиль. В итоге, после её применения, ряд имеет следующие характеристики:

Количество элементов: 761

Среднее арифметическое выборки: 1 021508

Среднеквадратическое отклонение: 184700.2

Минимум: 391828.4

Процентиль 25 % 941943.7

Процентиль 50 % 1014339

Процентиль 75 % 1139627

Максимум 1446973

Рассчитав по вышеописанной формуле, мы получаем коэффициент вариации равный 18 %, что свидетельствует об однородности исследуемого ряда. В итоге, данные, однородные, не имеют больших выбросов, оптимизированы и очищены, но для выбора модели прогнозирования определим стационарен ли рассматриваемый ряд с помощью теста Дикки-Фуллера.

Целью моделирования чаще всего является предсказание значений ряда. А если этот ряд принимает непрерывные значения, точечный прогноз неинформативен, и требуется пересмотреть подход к определению доверительной полосы при прогнозировании. Из-за этого и некоторых сложностей при построении модели вводится понятие стационарного ряда.

О стационарности временного ряда неформально можно говорить исходя из предметной области. Очевидно, что объем денежных средств относительно времени величина, не изменяющая свои статистические характеристики, соответственно мы можем сделать вывод на основе интуитивного подхода, что ряд стационарен.

С другой стороны, используя аппарат математической статистики, стационарность временного ряда можно установить, проверив равенство АКФ (попарное сравнение коэффициентов корреляции каждого порядка с помощью теста на равенство корреляции).

Описанный подход называется тестом Дики — Фуллера. Суть заключается в том, что наличие единичного корня берется за основу нулевой гипотезы, то есть нестационарность ряда. Также рассматривается альтернативная гипотеза о стационарности. Математически это можно описать как:

— на окружности лежит какой-либо корень характеристического полинома, ряд нестационарный

— единичного корня нет, ряд стационарный

Для проверки гипотезы воспользуемся средствами языка python.

В библиотеке statsmodels в языке python есть функция adfuller(), которая принимает на вход ряд, и проверяет гипотезу о наличии единичного корня и альтернативную ей. Функция проводит несколько тестов способных определить: результирующее значение теста adf; p-value, полученные с помощью аппроксимации поверхности регрессии; количество лагов; число наблюдений, используемых для регрессии и вычисления критических значений; критические значения для тестовой статистики на уровнях 1 %, 5 %, 10 %. Если значение превышает критический размер, нельзя отклонить гипотезу, что существует единичный корень. Тест показал следующие значения:

adf ~ -3.801

p-value: ~ 0.002

Критические значения 1 % ~ -3.439

5 % ~ -2.865

10 % ~ -2.568

На практике после получения этих данных рассматриваемую гипотезу можно отвергнуть сравнив результирующее и критическое значения. Если adf больше критического значения, то ряд не стационарен и имеет единичные корни. Полученные значения обратны этому, следовательно, в соответствии с тестом Дикки — Фуллера, который считается фундаментальным, единичных корней нет, а значит исследуемый ряд стационарен.

Возможность прогнозирования чего-либо является необходимым широко распространенным инструментом при процессе принятия решений, когда время и деньги непосредственно связаны между собой. При принятии стратегических решений в условиях неопределенности все делают прогнозы, в большинстве случаев выбор будет направлен на ожидание результатов действия или бездействия.

Можно классифицировать основные методы предсказания, которые часто применяются:

– Экспертные методы прогнозирования (Основывается на оценке эксперта, мнение которого в совокупности представляет единую оценку.)

– Статические методы (Предсказание строится на основе основных показателей описательной статистики: математическое ожидание, дисперсия, различные индексов, вариации.)

– Методы логического моделирования (Рассматриваются для долгосрочных прогнозов используя нахождение закономерностей и поиск)

– Экономико-математические методы (Создаются модели изучаемых областей, и предсказывается дальнейшее поведение при некоторых условиях.)

– Фундаментальный анализ (При прогнозировании анализу подвергаются основные финансовые показатели компании, и ее производительность.)

– Технический анализ (Предсказывает как изменятся значения в будущем на основе анализа изменения значений в прошлом)

После подробного изучения вариантов построения прогнозов, был выбран технический анализ. Так как в нем большое количество инструментов и методов, основанных на предположении о том, что при анализе временных рядов, выделив одну из его компонент — тренд, можно предсказать следующие значения. Всего во временном ряду при моделировании и анализе рассматриваются четыре компоненты:

– — тренд (плавное долгосрочное изменение уровня ряда)

– — сезонность (циклические изменения уровня ряда с постоянным периодом)

– — цикл (изменения уровня ряда с переменным периодом)

– — ошибка (непрогнозируемая случайная компонента ряда)

Наборы данных временных рядов могут содержать сезонную компоненту, иначе сезонные колебания. Это цикл, который повторяется регулярно со временем, например, ежемесячно или ежегодно. Он может снижать качество данных, либо же наоборот, предоставлять новые знания для повышения точности прогноза. То есть удаление сезонного колебания из временного ряда может привести к более четкой взаимосвязи между входными и выходными переменными. В рассматриваемой задаче определение сезонной компоненты может предсказать периоды гриппа, обязательного прохождение мед. осмотра, эпидемии.

Определение периода сезонности субъективно так, как их можно сколько угодно уменьшать и увеличивать. Самый простой подход к его определению — это анализ в различных масштабах и с добавлением линий тренда. Модель сезонности может быть удалена из временных рядов. Этот процесс называется сезонной корректировкой или дезаминированием. Простым способом корректировки сезонного компонента является использование разности. Если он наблюдается на уровне одной недели, то можно удалить его на текущем дне, вычитая значение с прошлой недели.

Временной ряд имеет явную модель сезонности, а также общую тенденцию увеличения. Мы также можем визуализировать наши данные с помощью метода, называемого декомпозицией временных рядов. Как следует из названия, декомпозиция временных рядов позволяет нам разложить наши временные ряды на три отдельных компонента: тренд, сезонность и шум. Библиотека statsmodels предоставляет удобную функцию seasonal_decompose() для выполнения сезонной декомпозиции:

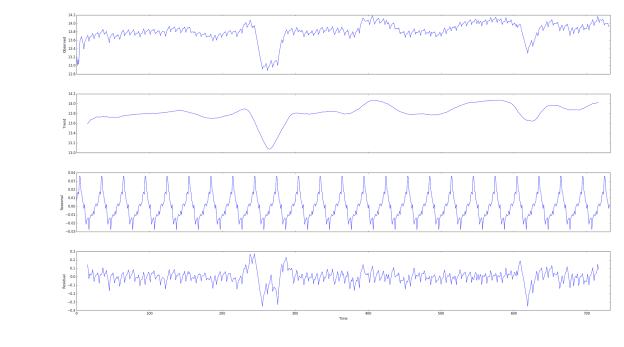
Рис. 5. Общий график, тренд, сезонная компонента, шум

На рисунке 5 четко просматривается тенденция к росту наших данных, а также ее сезонная компонента. Они могут быть использованы для понимания структуры исходного временного ряда. Наличие этих компонент важно для разложения временных рядов, поскольку многие методы прогнозирования основываются на этой концепции структурированной декомпозиции для получения прогнозов.

Проводимые тесты показали, что в исходном ряде присутствуют трендовая и сезонная компоненты. Рассматривая предметную область, мы также смело можем предположить, что они все же есть так, как есть определенные сезоны, когда прогрессирует грипп и число обращений в медучреждение увеличивается, прохождение медицинского осмотра перед учебным годом учеников и учителей. Также можно сделать предположение, что тренд присутствует и период его равен году так, как вначале каждого года количество обращений в больницы уменьшается. Это подтверждают и спады на графике тренда.

На исходных данных это не особо сказывается из-за достаточно малой выборки, в дальнейшем при накоплении большего объема информации, можно сделать предположение, что эти компоненты будут оказывать большее влияние. В связи с этим стоит рассматривать модели прогнозирования временных рядом способные адаптировать свои методы с учетом тренда и сезонности.

Модели временных рядов называются иначе стохастическими моделями. На сегодняшний день существует более ста различных методов построения моделей. Рассмотрим наиболее популярные применимые для стационарных временных рядов:

1. Регрессионные модели.

Сюда входят линейная, множественная и нелинейная регрессии. Пусть — множество параметров, — множество зависимых переменных, — множество свободных переменных. Тогда задает отображение:

Недостатком регрессионного анализа является то, что сложные модели могут переобучаться, а модели, имеющие слишком малую сложность, могут оказаться неточными.

2. Модели экспоненциального сглаживания.

Применяется только для прогнозирования на один период вперед, и наиболее эффективен для среднесрочных прогнозов. Пусть — период веса, которого мы хотим учитывать; — период, который нужно предсказать; — экспоненциально взвешенная средняя для ряда; — параметр сглаживания; — значение ряда. Тогда прогнозируемый показатель можно вычислить по формуле:

Этот метод нельзя применять для среднесрочного и долгосрочного прогнозирования. Также недостатком является то, что он не учитывает сезонные и случайные колебания.

3. Модели по выборке максимального правдоподобия.

Метод предполагает, что для каждой выборки, предшествующей прогнозу, есть похожая выборка. Она содержится в фактических значениях временного ряда. Функция правдоподобия имеет вид:

Для построения прогноза нужно максимизировать значение функции правдоподобия, из множества моделей, то есть выбрать . Недостатком такой модели, является то, что достаточно точные результаты получаются на узком кругу задач, хотя применим этот метод к большинству задач для оценки параметров.

4. Модель на нейронных сетях

Этот подход является громоздким, непрозрачным и достаточно сложным. Чаще всего он используется для распознавания образов, но и в классе задач для прогнозирования показывает высокую эффективность. Недостатком является то, что у разработчика есть возможность формировать входы и наблюдать выходы, но нет возможности проследить как рассчитываются эти значения. То есть нет доступа к тому, что происходит внутри сети. К тому же такие модели требуют большую выборку данных.

5. Авторегрессионные модели прогнозирования

Моделирование основывается на предположении, что последующие или предшествующие значения коррелируют с текущим. Причем прослеживается тенденция к тому, что близко лежащие оказывают большее влияние нежели далеко стоящие, то есть ряд коррелирует сам с собой.

Автокорреляция некоторого порядка и степень связности откликов, разделенных на то же число периодов, относятся к друг другу. То есть механизм прогнозирования основывается на связи между значениями и тому, что она сохранится в дальнейшем.

Пусть — порядок модели, тогда авторегрессионные модели можно записать как:

,

где — отклик в момент , — отклик на периодов раньше, — коэффициенты авторегрессии, — случайная компонента.

Недостатком является то, что для построения точной модели необходимо определить ее порядок, а это не так просто. И грань между упрощением модели и точностью прогнозов достаточно сложно определить.

В нашей задаче при выбранных методах предварительной обработки в соответствии с классификацией должна быть выбрана модель ARIMA. Несмотря на недостатки все же эта модель показывают высокую точность на среднесрочных прогнозах. К тому же она способна адаптировать свои методы в зависимости от свойств исходного временного ряда. Это наиболее актуально в нашем случае так, как связи с тем, что количество данных со временем увеличится, и возможно появится трендовая компонента и сезонная компонента, это является следствием проведенного анализа данных.

В результате работы был приведен алгоритм предварительной обработки данных учитывая предметную область рассматриваемой темы. Рассмотрены экономические подходы к решению задачи, проведен анализ данных, выбрана ключевая выборка. Выполнена предварительная подготовка данных, путем устранения дубликатов и противоречий, восстановления целостности, оптимизации данных. К полученному ряду применен метод экспоненциального сглаживания. Произведено исследование временного ряда на стационарность с помощью различных тестов, в частности Дикки-Фуллера. Проведен анализ трендовой и сезонной компоненты, однородности значений и выбросов. Рассмотрены и проанализированы математические модели применимые к рассматриваемой задаче, приведены их недостатки и достоинства. Все рассмотренные методы предварительной обработки, анализа данных реализованы на языке python с использованием библиотек statsmodels, pandas, scikit-learn. Для визуального представления данных использована библиотека matplotlib.

Литература:

1. Тарасов Ю. И. Перспективы развития обязательного медицинского страхования // Экономика здравоохранения, 2004. № 3. C. 18–21.
2. Тарифное соглашение в сфере обязательного медицинского страхования по Краснодарскому краю http://www.kubanoms.ru/_files/normativnaya_baza/ts/2017/ts_2017_.pdf
3. Федеральный закон от 21 ноября 2011 г. N 323-ФЗ «Об основах охраны здоровья граждан в Российской Федерации» http://base.garant.ru/12191967/
4. Cielen D., Meysman A., Ali M. Introducing Data Science Big Data, Machine Learning, and more, using Python tools, 2016. 22–48 c.
5. Holt C. C. Forecasting trends and seasonals by exponentially weighted moving averages, 1957.
6. Бокс Дж., Дженкинс Г. Анализ временных рядов: прогноз и управление. Выпуск 1. М.: Мир, 1974. C. 144–164
7. Тихонов Э. Е. Методы прогнозирования в условиях рынка, 2006. М.: Наука. С. 11–49.
8. Documentation Statsmodels python http://www.statsmodels.org/stable/index.html
9. Documentation Pandas python http://pandas.pydata.org/pandas-docs/version/0.15.2/tutorials.html
10. Documentation scikit-learn python http://scikit-learn.org/stable/tutorial/index.html