В работе рассматривается прогнозирование продаж с помощью нескольких моделей прогнозирования, задачи связанные с несвоевременным пополнением магазинов, а также анализ возникновения излишних остатков на складе и их оптимизация.
Ключевые слова: модель прогнозирования Хольта, Брауна, Уинтерса, Байесовский алгоритм, сезонность, авторегрессия, фактические и плановые продажи, оптимизация
На данный момент мировой опыт показывает необходимость наличия финансово доступной и мобильной системы прогнозирования рынка, товаров и услуг, как важный механизм адаптации и планирования перспективного развития любой торговой сферы. В условиях интенсивно развивающихся рыночных отношений и глобализации очень важно проводить анализ, прогноз и планирование взаимоотношений с клиентами, а также резервов складских помещений и сетевого распределения товаров, в зависимости от множества переменных данных. Зачастую малые торговые учреждение осуществляют прогноз и оптимизацию товаров на основе накопленного опыта. Но для начинающего бизнеса решение этих вопросов может вызывать значительные трудности в связи с недостаточностью знаний или отсутствием опыта. Подобные модули уже существуют в системе 1С, SAP и Microsoft. Однако их стоимость может быть препятствием для использования в малом бизнесе. Более эффективным и доступным будет создание автономного модуля, который будет учитывать следующие математические модели:
− тренд;
− сезонность;
− факторы, влияющие на спрос: праздничные дни, рекламные акции, изменение цены, местные события, детерминированные потребности.
Также анализировать успешность:
− прогноз продаж за этот, предыдущий и следующий год;
− анализ продаж за этот, предыдущий и следующий год.
При управлении процессом продаж в любой компании во главу угла ставится вопрос о том, как продать товара как можно больше по выгодной цене, минимизировать издержки на транспортировку и хранение товара и получить большую прибыль. Существуют несколько прогнозных моделей:
− в простейшей прогнозной модели рассматривается реакция на импульс, линейное и параболическое воздействие;
− модели Хольта и Брауна используются тогда, когда временной ряд имеет тенденцию временного роста;
− Байесовский алгоритм используется для при внутрисезонном прогнозировании, т. е. когда по фактическим продажам в течение текущего сезона уточняется ранее найденные с помощью других методов предсезонным прогноз на будущую часть текущего сезона. Отметим, что название алгоритма (в оригинале «Bayesian algorithm») к классической в теории вероятностей формуле Байеса никакого отношения не имеет [1].
В данном модуле используются 3 модели прогнозирования:
− Линейная регрессия
− Регрессия второго порядка
− Регрессия третьего порядка.
Линейная регрессия предназначена для получения прогноза непрерывных числовых переменных.
Достоинства линейной регрессии:
− Скорость и простота получения модели.
− Интерпретируемость модели. Линейная модель является прозрачной и понятной для аналитика. По полученным коэффициентам регрессии можно судить о том, как тот или иной фактор влияет на результат.
− Широкая применимость. Большое количество реальных процессов в экономике и бизнесе можно с достаточной точностью описать линейными моделями.
− Изученность данного подхода.
Регрессия — это условное математическое ожидание непрерывной зависимой (выходной) переменной при наблюдаемых значениях независимых (входных) переменных. Линейная регрессия основана на гипотезе, что искомая зависимость — линейная. Каждая независимая переменная вносит аддитивный вклад в результирующее значение с некоторым весом, называемом коэффициентом регрессии.
Математическое уравнение, которое оценивает линию простой (парной) линейной регрессии:
![]() ,(1)
,(1)
Для получения вида математической модели необходимо определить коэффициенты уравнения регрессии b0 и b1. Для этого применяется метод наименьших квадратов.
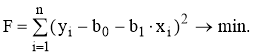 (2)
(2)
Таким образом, процедура нахождения коэффициентов регрессии сводится к задаче определения минимума функции. Необходимое условие минимума функции является равенство нулю частных производных функции по исходным величинам (коэффициентам).
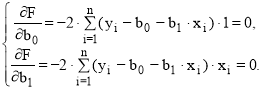 (3)
(3)
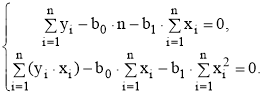 (4)
(4)
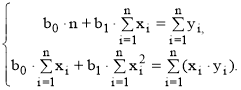 (5)
(5)
Решая систему уравнений (5), выражаем коэффициенты b0 и b1.
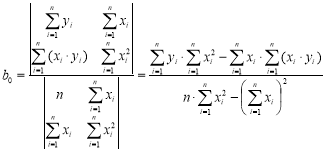 (6)
(6)
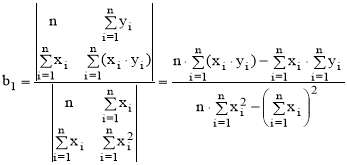 (7)
(7)
После вычисления коэффициентов необходимо провести статистический анализ полученного уравнения регрессии с целью проверки модели на адекватность.
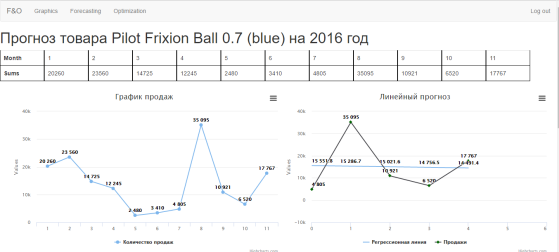
Рис. 1. График продаж и линия линейной регрессии
На рисунке 1 отображена таблица количество продаж товара по месяцам, также изображены два графика. С левой стороны отображен график продаж на 2016 год, а справа — линейная регрессия по последним пяти месяцам. По линейной регрессии можно сделать вывод об увеличении или уменьшение продаж. В данном случае линия и не возрастает, и не убывает. Для того, чтобы уточнить возрастают или убывают продажи построим линейную регрессию по последним 7 ми точкам рис. 2
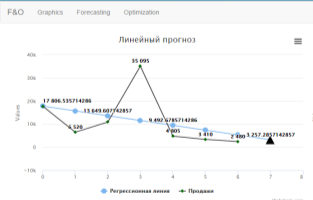
Рис. 2. Линия линейной регрессии по семи точкам
На рисунке 2 по линии линейной регрессии видно, что продажи убывают. Последняя выделенная точка — это прогноз на следующий месяц.
Для выявления точности прогноза необходимо сравнить несколько методов. Рассмотрим метод регрессии второй степени. Математическое уравнение, которое оценивает линию регрессии второго порядка:
![]() (8)
(8)
Коэффициенты регрессии определяем по методу наименьших квадратов.
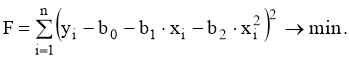 (9)
(9)
Приравняем к нулю частные производные функции по коэффициентам b0, b1, b2.
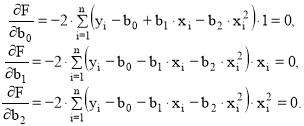 (10)
(10)
Выполнив преобразования (10), получим систему линейных уравнений с тремя неизвестными (b0, b1,b2).
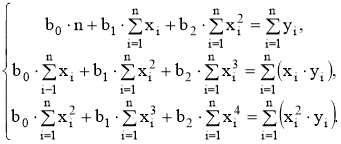 (11)
(11)
Введем обозначения:
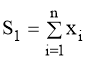 ;(12)
;(12)
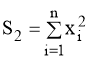 ;(13)
;(13)
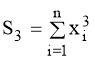 ;(14)
;(14)
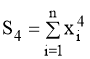 (15)
(15)
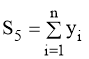 ;(16)
;(16)
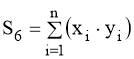 ;(17)
;(17)
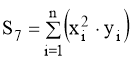 .(18)
.(18)
С учетом принятых обозначений система будет иметь следующий вид:
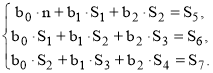 (19)
(19)
Определим неизвестные коэффициенты b0, b1, b2.
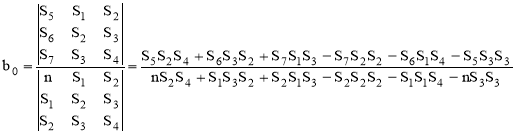 (20)
(20)
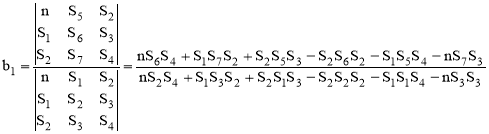 (21)
(21)
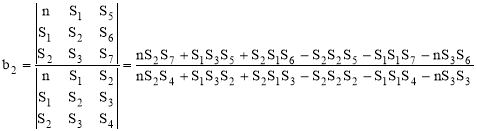 .(22)
.(22)
После решения системы уравнений (11) и вычисления коэффициентов b0, b1, b2 проводится статистический анализ полученного уравнения регрессии. Аналогичным образом будут определяться коэффициенты параболы любого порядка. Исследование уравнения проводится по статистическим критериям. Однако в этом случае не требуется вычислять выборочные коэффициенты корреляции. Адекватности уравнения регрессии эксперименту можно добиться, повышая степень полинома. Однако при этом все коэффициенты следует вычислять заново, так как существует корреляция между коэффициентами.
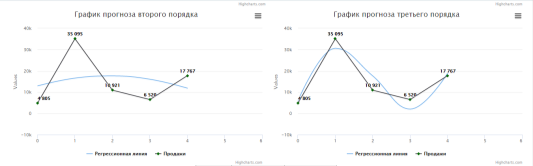
Рис. 3. Линия регрессии второго и третьего порядка
На рисунке 3 слева изображен график регрессии второго порядка, справа — третьего. По изображения регрессии второго порядка можно сделать вывод, что продажи убывают, так как парабола смотрит вниз, а в регрессии третьего порядка линия проходит через каждую точку и не совсем понятно, куда стремится линия. Поэтому необходимо рассмотреть линию по семи точкам рис. 4.
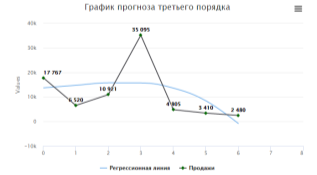
Рис. 4. Линия регрессии третьего порядка для семи точек
На рисунке 4 по линии регрессии видно, что продажи убывают.
Для того, чтобы узнать какая из данных моделей осуществляет более точный прогноз на следующий месяц, необходимо рассчитать ошибку аппроксимации. Чем меньше ошибка, тем точнее прогноз.

Рис. 5. Расчет ошибки для пяти точек
На рисунке 5 показано, что наименьшая ошибка у третьей модели, т. е. регрессии третьей степени.
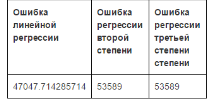
Рис. 6. Расчет ошибки для семи точек
На рисунке 6 показано, что наименьшая ошибка у первой модели, т. е. линейной регрессии.
Для того, чтобы узнать какие из графиков точнее прогнозируют, необходимо осуществить верификацию данных, т. е. сделать прогноз для старых данных, например, для 2015 года, и сравнить и нынешними данными.
В модели Хольта коэффициенты линейной модели
![]() (23)
(23)
модифицируются по следующим соотношениям:
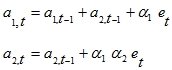 (24)
(24)
Начальные значения параметров модели находятся по МНК на основе нескольких первых наблюдений. Оптимальные значения параметров сглаживания ![]() находятся в переделах от нуля до единицы. Они определяются методом многомерной численной оптимизации и являются постоянными для всего периода наблюдений.
находятся в переделах от нуля до единицы. Они определяются методом многомерной численной оптимизации и являются постоянными для всего периода наблюдений.
Аналогично модели Брауна, модель Хольта в терминах АРСС-моделей представима в виде:
Формулировка адаптивных моделей в терминах линейных параметрических моделей авторегрессии — скользящего среднего позволяет трактовать их как подмножество класса линейных параметрических моделей. Таким образом, устанавливается соответствие между двумя, вообще говоря, различными подходами к моделированию временных рядов.
В таблице параметров модели для модели Хольта отображаются оптимальные значения коэффициентов ![]() .
.
Пусть ![]() — временной ряд наблюдений. Прогноз в момент времени t на
— временной ряд наблюдений. Прогноз в момент времени t на ![]() шагов вперед может быть получен по формуле:
шагов вперед может быть получен по формуле:
![]() (26)
(26)
где![]() и
и ![]() — текущие оценки коэффициентов адаптивного полинома.
— текущие оценки коэффициентов адаптивного полинома.
В модели Брауна модификация (адаптация) коэффициентов линейной модели осуществляется следующим образом:
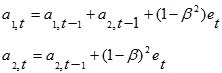 (27)
(27)
где ![]() — коэффициент дисконтирования данных;
— коэффициент дисконтирования данных;
![]() — ошибка прогнозирования,
— ошибка прогнозирования,
![]() (28)
(28)
Начальные значения параметров модели определяются по МНК на основе нескольких первых наблюдений. Оптимальное значение параметра дисконтирования находится в переделах от нуля до единицы, определяется методом численной оптимизации и является постоянным для всего периода наблюдений.
Оператор В сдвигает всю последовательность на один шаг назад: Bx(t)=x(t-1). Применение оператора В к наблюдениям и к коэффициентам адаптивного полинома позволяет выразить модель Брауна в виде:
![]() (29)
(29)
из чего следует, что модель Брауна можно трактовать как модель авторегрессии — скользящего среднего АРСС(p,d,q) с p=0, d=2, q=2 и коэффициентами скользящего среднего ![]() .
.
− прогнозные модели Уинтерса предназначены для прогнозирования временных рядов, содержащих периодические сезонные составляющие;
Мультипликативная модель Уинтерса аналогична с той лишь разницей, что расчетные по линейной модели значения корректируются путем их умножения на сезонные коэффициенты. Прогноз на ![]() шагов вперед строится по формуле:
шагов вперед строится по формуле:
![]() (30)
(30)
а модификация параметров производится по соотношениям:
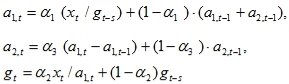 (31)
(31)
Где g — фактор сезонности, s — период сезонного цикла.
Для несезонных временных рядов вычислительные формулы упрощаются за счет исключения сезонной компоненты. При построении модели производится численная оптимизация параметров адаптации, значения которых изменяются от нуля до единицы [3].
Все описанное выше относится только к продуктам, которые уже имеют историю продаж. Если же продукт новый, то истории, очевидно, нет. Поэтому применяют другие методы, одним из которых является перемножение off-take и АКБ. Под термином off-take понимается объем продаж продукта конкретного магазина конечным потребителем. Понятно, что оба эти показателя надо каким-то образом вычислять. Для определения off-take обычно используют либо данные агентств, собирающих такую информацию, либо собственного аудита розницы. Если компанию интересует вычисление off-take собственного продукта, то можно исходить из предложения, что магазин закупает в среднем примерно столько продукций, сколько и продает. Таким образом, выбрав из собственной аналитической системы средние продажи продукта в торговые точки определенного типа, мы получаем аппроксимацию off-take в точках данного типа. Очевидно, что умножив этот показатель на число магазинов, т. е. на АКБ, мы снова получим объем продаж. Данные можно выбрать как из первичных, так и из вторичных продаж. Но это применимо к уже продающимся продуктам, а нам нужно оценить off-take продукта нового. Для этого придется обратиться к данным агентства [3].
В случаях, когда продукта нет у конкурентов или в данных аудита, и в других случаях, когда нет четкого ответа на интересующий нас вопрос, проводятся исследования, и на основании результатов делаются расчеты. При этом важно не забыть, что если продукт продается через дистрибуторов, первые отгрузки будут значительно выше прогнозируемых продаж, так как происходит заполнение их складов. Затем следует резкое падение, и только потом продажи постепенно выходят на планируемый уровень.
Прогнозирование новых продуктов почти всегда отличается низкой точностью, так как является крайне сложным. Тем не менее, первые несколько месяцев продаж, пока не будет накоплено достаточно данных для экстраполяции тренда, компании придется довольствоваться такой точностью.
Любая солидная компания планирует объем продаж на предстоящий сезон. Этот план определяет закупочную стратегию компании. Если фактические продажи от плановых, то компания вынуждена вводить дополнительные скидки на товар, чтобы избежать затоваривания складских помещений и обеспечить место под новые коллекции товара. Возникает вопрос об определении этих скидок и моментов времени, в которые эти скидки нужно вводить.
Целевым образом можно установить, что:
− Скидки могут вводиться не чаще, чем раз в две недели;
− Скидки с течением времени не могут уменьшаться.
Задача, которая касается продажам сезонных коллекций товара и связана с поиском оптимального распределения торговой площади между старыми и новыми коллекциями товаров в период межсезонья, под критерием оптимальности выступает как максимизация выручки от продаж.
Проблема связанная с анализом и управлением остатками товара межсезонья состоит в том, что поступление коллекций нового сезона происходит не одномоментно, а распределено во времени. В связи с этим в магазинах всегда должен быть некоторый запас старых коллекций, чтобы не допустить такой ситуации, когда нечего будет выложить на прилавок, если процесс продаж старых коллекций будет опережать процесс поступления новых. Другими словами в период межсезонья должен существовать некий баланс между остающимися в магазине старыми коллекциями и вновь поступающими новыми.
Также есть задачи связанные с несвоевременным пополнением магазинов. Дело в том, что из-за транспортных, таможенных, политических и других проблем товар не может поступать в магазины с отставанием от планового графика. Поэтому возникает задача оценки прогнозируемых остатков товара на какой-либо определенный момент, а также оценки оптимального объема завозимого товара в зависимости от режима пополнения товара.
Для осуществления бесперебойного производственного процесса, для начала, необходимо проанализировать предпосылки возникновения излишних остатков на складе [5]:
− Приобретение предпринимателем заведомо превосходящего необходимое количества товара в связи с риском неполной доставки или задержки в пути.
− Наличие привлекательных акционных цен на оптовые партии товаров
− Экономия на транспортных расходах: намного дешевле обходится привезти один раз большую партию, чем несколько раз мелкие.
Кроме того, нужно учесть такие факторы:
− Скачкообразное увеличение товарного спроса в ходе всего срока его реализации.
− Непостоянство сроков восполнения запасов.
Оптимизация складских процессов осуществляется в следующем порядке.
Анализ конкретной компании с целью выяснения его «уязвимых мест. Анализ взаимодействия складского и смежных с ним процессов (сбыт, закупки, доставка, информационное обеспечение) позволяет выявить проблемы и ранжировать их по значимости, подобрав наиболее оптимальный способ их устранения.
Таким образом, были рассмотрены графические отображения нескольких моделей прогнозирования: линейная регрессия, регрессия второго порядка и регрессия третьего порядка, где определяется наиболее точный метод прогноза. Выявлено, что в зависимости от истории продаж, один и тот же метод может давать разные варианты прогноза. В конечном итоге следует отметить, что точность прогноза имеет прямую корреляцию с объемом истории продаж. Чем длиннее история продаж, тем точнее происходит прогнозирование.
Литература:
- Семаков С. Л., Семаков А. С. Прогнозирование и управление продажами в торговых сетях. — М.: ФИЗМАТЛИТ,2012. — 144 с.
- Горчелс Л. Управление каналами дистрибуции. — М.: Издательский Дом Гребенников, 2005. – 248 с.
- Гусаков И. Анализ и планирование продаж в компаниях рынка FMCG/Игорь Гусаков. – М.: Книга по Требованию, 2014. – 272 с.
- Википедия [Электронный ресурс]. — URL: http://www.machinelearning.ru/wiki
- Управление запасами [Электронный ресурс]. — URL:http://upravlenie-zapasami.ru/statii/optimizaciya-poshtuchnoy-sborki-tovara-na-sklade/







