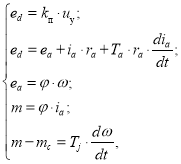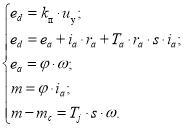Основные дифференциальные уравнения силовой части системы «Тиристорный преобразователь – двигатель постоянного тока независимого возбуждения» (ДПТ НВ) в системе относительных единиц имеют следующий вид [1]:
|
|
(1) |
где![]() - ЭДС тиристорного преобразователя;
- ЭДС тиристорного преобразователя;
![]() - управляющее воздействие;
- управляющее воздействие;
![]() - ЭДС якоря двигателя;
- ЭДС якоря двигателя;
![]() - электромагнитный момент двигателя;
- электромагнитный момент двигателя;
![]() - скорость вращения якоря;
- скорость вращения якоря;
![]() - статический реактивный момент (возмущающее воздействие).
- статический реактивный момент (возмущающее воздействие).
1. Модель системы ТП - ДПТ НВ в Matlab-Simulink.
Для моделирования в Matlab-Simulink необходимо перевести эти уравнения к изображениям, для этого заменяем оператор дифференцирования оператором s. В этом случае система уравнений (1) преобразуется к виду:
|
|
(2) |
Из которых выразим ia и ω:
![]()
Математическая модель системы ТП - ДПТ НВ в Matlab-Simulink представлена на рис. 1. Сигналы задания управляющего воздействия uу и статического момента mc в блоке Signal Builder приведены на рис. 2.
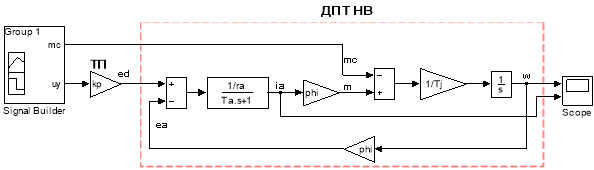
Рис. 1. Математическая модель системы ТП - ДПТ НВ в Matlab-Simulink
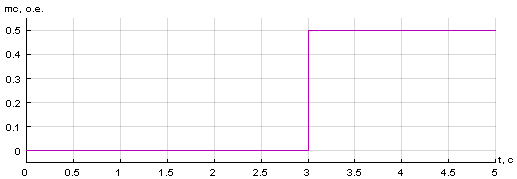
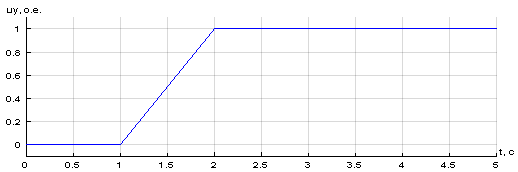
Рис. 2. Сигналы задания статического момента mc и управляющего воздействия uу
Зададимся исходными данными:
![]() - коэффициент передачи преобразователя (ТП);
- коэффициент передачи преобразователя (ТП);
![]() - сопротивление якорной цепи, о.е.;
- сопротивление якорной цепи, о.е.;
![]() - электромагнитная постоянная времени цепи якоря, с;
- электромагнитная постоянная времени цепи якоря, с;
![]() - инерционная постоянная времени механической части привода, с.
- инерционная постоянная времени механической части привода, с.
Результаты моделирования ТП - ДПТ НВ в Matlab-Simulink даны на рис. 3.
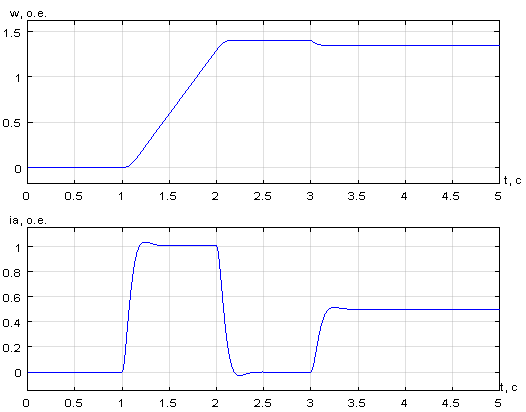
Рис. 3. Графики скорости ω и тока ia в Matlab-Simulink
2. Моделирование ТП - ДПТ НВ в Matlab-Script.
При решении в Matlab-Script необходимо в системе (1) заменить дифференцирование переменных конечными разностями этих переменных:
![]()
![]()
Отсюда ток ![]() определится:
определится:
![]()
Аналогично для скорости ω:
![]()
![]()
Тогда математическая модель ТП - ДПТ НВ в Matlab-Script будет иметь следующий вид (листинг 1):
Листинг 1
ra=0.107;Ta=0.034;kp=1.4;phi=1;Tj=0.72;
ia(1)=0;w(1)=0;ea(1)=0;dt=0.001;t=0;
t1=5;tn=1;tk=2;
cnt=t1/dt;
for i=1:cnt
if(t>=3)
mc=0.5;
else
mc=0;
end;
if((t>=tn)&&(t<=tk))
uy=(t-tn)/(tk-tn);
elseif(t>=tk)
uy=1;
else
uy=0;
end;
ed(i+1)=kp*uy;
ia(i+1)=ia(i)+(ed(i+1)-ea(i)-ia(i)*ra)*dt/(Ta*ra);
m(i+1)=phi*ia(i+1);
w(i+1)=w(i)+(m(i+1)-mc)*dt/Tj;
ea(i+1)=phi*w(i+1);
t=t+dt;
mass_t(i)=i*dt;
mass_w(i)=w(i+1);
mass_ia(i)=ia(i+1);
end;
figure(1);
plot(mass_t,mass_w,'b');
grid on;
figure(2);
plot(mass_t,mass_ia,'r');
grid on;
Результаты моделирования ТП - ДПТ НВ в Matlab-Script приведены на рис. 4.
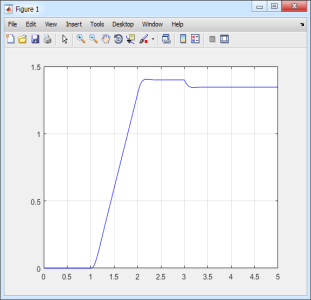
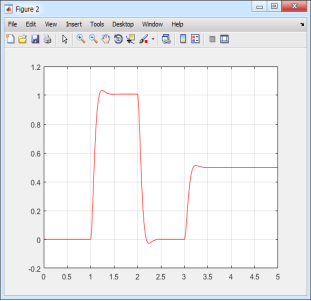
Рис. 4. Графики скорости ω и тока ia в Matlab-Script
3. Моделирование ТП - ДПТ НВ на языке программирования Си.
Математическая модель системы ТП - ДПТ НВ на языке программирования Си приведено в листинге 2.
Листинг 2
#include
#undef __STRICT_ANSI__
#include
#include "gnuplot_i.h"
#define FILENAME "tmp.txt"
int main(void) {
// параметры двигателя постояного тока
const double ra = 0.107, // сопротивление обмотки якоря, о.е.
Ta = 0.034, // электромагнитная постоянная времени цепи якоря двигателя, с
kp = 1.4, // коэффициент передачи преобразователя
phi = 1, // номинальный магнитный поток
Tj = 0.72, // электромеханическая постоянная времени
K = 1000, // коэффициент усиления задатчика интенсивности
Ti = 0.01, // постоянная времени интегратора
A = 1; // темп изменения выходного сигнала задатчика интенсивности
// переменные математической модели двигателя постоянного тока
double uy = 0, // управляющее воздействие
ed = 0, // эдс преобразователя
ea = 0, // эдс двигателя
m = 0, // электромагнитный момент двигателя
mc = 0, // момент статического сопротивления
ia = 0, // ток якоря
w = 0, // скорость вращения
uy_zad = 0, // сигнал задания по напряжению
duy = 0, // разность между входным и выходным сигналами задания
Kduy = 0,
Qmax = 0, // уровень насыщения задатчика интенсивности
Q = 0; // выходной сигнал задатчика интенсивности
double dt = 1e-3; // шаг интегрирования
double t = 0; // текущее значение времени
double t1 = 5; // конечное значение времени расчета
unsigned int cnt = t1/dt; // количество точек
// Создаем временный файл, в который будем записывать текущие значения
FILE *fp = fopen(FILENAME, "w");
// цикл расчета
for (unsigned int i = 0; i < cnt; i++) {
// подача управляющего воздействия
if (t >= 1.0f)
uy_zad = 1.0f;
else
uy_zad = 0.0f;
// расчет мат. модели задатчика интенсивности
duy = uy_zad - uy;
Kduy = K * duy;
Qmax = A * Ti;
if (Kduy > Qmax)
Q = Qmax;
if ((-Qmax <= Kduy)&&(Kduy <= Qmax))
Q = Kduy;
if (Kduy < -Qmax)
Q = -Qmax;
uy = uy + (Q / Ti) * dt;
// подача возмущающего воздействия
mc = (t >= 3.0f)? 0.5f: 0.0f;
// расчет мат модели двигателя пост тока
ed = uy * kp;
ia = ia + dt * (ed - ea - ra * ia) / (ra * Ta);
m = ia * phi;
ea = w * phi;
w = w + dt * (m - mc)/Tj;
// записываем точки во временный файл
fprintf(fp,"%f\t%f\t%f\t%f\n", t, ia, w, uy);
// увеличиваем переменную время
t = t + dt;
}
// Закрываем текстовый файл с текущими значениями
fclose(fp);
// Рисуем графики
gnuplot_ctrl *h;
h = gnuplot_init();
gnuplot_cmd(h, "set grid xtics ytics"); // вкл сетка
gnuplot_cmd(h, "plot '%s' u 1:2 w li lt rgb 'red' ti 'ia',\
'%s' u 1:3 w li lt rgb 'blue' ti 'w',\
'%s' u 1:4 w li lt rgb '#008000' ti 'uy'", FILENAME, FILENAME, FILENAME);
getchar();
gnuplot_close(h);
// Удаляем временный файл с точками
if (!remove(FILENAME))
printf("Deleting file is complete\n");
else
printf("Temp file does not delete\n");
return 0;
}
Результаты моделирования ТП - ДПТ НВ на языке Си приведены на рис. 5.
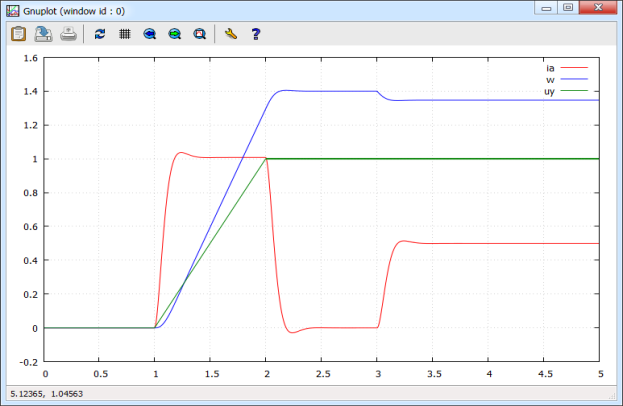
Рис. 5. Графики скорости ω и тока ia на языке программирования Си
Литература:
- Шрейнер Р.Т. Системы подчиненного регулирования электроприводов: учеб. пособие / Р.Т. Шрейнер. - Екатеринбург: Изд-во ГОУ ВПО «Рос. гос. проф.-пед. ун-т», 2008. – 279 с.
- Васильев А.Н. Matlab. Самоучитель. Практический подход. – СПб.: Наука и Техника, 2012. – 448 с.
- Васильев А.Н. Программирование на C++ в примерах и задачах. – М.: Издательство «Э», 2017. – 368 с.